【自己出题】水滴(ST表,树)
题目
描述
在学校的路旁,有两排树,一排是杏树,另一排也是杏树。
每棵树可以看作是由\(n\)个点和\(n-1\)条枝条构成的。一个雨滴落在了一棵树上的点\(u\),他在重力的牵引下向下流动。他每秒都会流过一条边,直到抵达根节点,融进大地。
他漫无目的地向下移动,在\(t\)秒后,他突然和另一滴雨撞在了一起。刹那间,他的电子飞速运动,思考着与他相碰的这个雨滴最初可能是落在了哪些点上。
输入
第一行有一个整数\(n(1\le n \le 10^5)\),表示树的节点数。树的根节点是\(1\)。
第二行有\(n-1\)个整数,其中第\(i\)个整数\(a_i(1\le a_i \le i)\)表示一条树枝的两个端点是\(i+1\)和\(a_i\)。
第三行有一个整数\(T(1\le T \le 10^5)\),表示数据组数。
接下来\(T\)行,每行有两个整数\(u,t(1\le u \le n; 0\le t \le n)\),保证数据合理。
输出
共\(T\)行,每行一个整数,表示答案。
sample
input
5
1 2 2 4
1
3 1
output
3
hint
对于样例一,
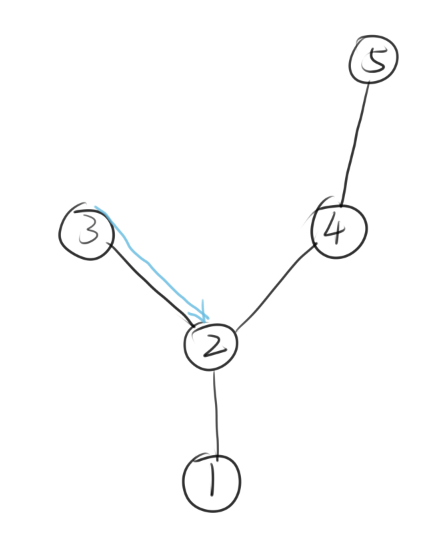
另一滴水可能是从2,4,5这三个点掉落的。
题解
设一个以a为根节点的子树,它包含结点的个数为size[a]。如果t=0,那么答案为size[u];否则,设u的第t-1个父亲是v,第t个父亲是fa[v],那么答案是size[fa[v]]-size[v]。
size数组和fa数组进行一遍dfs,很容易求出来。重点在于如何快速求出u的第x个父亲。
这个问题可以用ST表解决。即令f[u][i]表示u的第\(2^i\)个父亲是哪个点,i的范围是0~20,f数组可以在dfs的过程中求出来,方程是:
接下来就可以在O(log(t))的时间复杂度内求出u的第t个父亲。例如,t=11,它写成二进制是1011B,其中第0、1、3位是1,那么要求的结点就是 f[ f[ f[u][0] ][1] ][3]。
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
vector<int> V[N];
int n;
int sz[N], f[N][20], dep[N];
void Add(int u, int v){
V[u].push_back(v);
V[v].push_back(u);
}
void dfs(int u, int fa){
sz[u]=1;
for(int i=1; i<20; ++i) f[u][i]=f[f[u][i-1]][i-1];
for(auto&v:V[u]){
if(v==fa) continue;
f[v][0]=u;
dfs(v,u);
sz[u]+=sz[v];
}
}
int getlca(int u, int len){
for(int i=0; i<20; ++i) if(len&(1<<i)) u=f[u][i];
return u;
}
int main(){
scanf("%d", &n);
for(int i=2, fa; i<=n; ++i){
scanf("%d", &fa);
Add(i,fa);
}
dfs(1,0);
//t
int T; cin>>T;
while(T--){
int u, t;
scanf("%d%d", &u, &t);
if(t==0) printf("%d\n", sz[u]);
else{
int v=getlca(u,t-1);
printf("%d\n", sz[f[v][0]]-sz[v]);
}
}
}
数据生成
造数据有一个原则,那就是大小要小,否则上传数据就要耗费半天。因此我只造了6个数据,总大小为5M多,上传得还算快。
其中5个都是n=100000级别的数据,当然要随机生成了。
我通过控制每个节点与父节点标号的差的范围来控制树的形状,主要有下面三种情况:
对于每个结点i+1的父亲,一种情况是random(1,i),这样的树是完全随机生成的,我也不知道长什么样子;一种是random(1,min(i,50)),这样的树是非常扁平的;一种是random(max(1,i-100),i),这样的树是很高的。
我还构造了一个n=1的特别的测试点:
1
2
1 0
1 0
它的答案应该是:
1
1
数据生成代码:
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
mt19937 rnd(time(0));
vector<int> V[N];
int rand(int l, int r){
if(l==r) return l;
return rnd()%(r-l)+l;
}
int n, T;
int sz[N], dep[N];
FILE *fw;
void dfs(int u, int fa){
// printf("u=%d fa=%d\n", u, fa);
sz[u]=1; dep[u]=dep[fa]+1;
for(auto&v:V[u]) if(v!=fa){
dfs(v,u);
sz[u]+=sz[v];
}
}
void fun(){
n=100000;
fprintf(fw, "%d\n", n);
for(int i=1; i<=n; ++i){
V[i].clear();
sz[i]=0;
dep[i]=0;
}
for(int i=1, u; i<n; ++i){
fprintf(fw, "%d%c", u=rand(1,min(i,50)), " \n"[i==n-1]);
V[u].push_back(i+1);
V[i+1].push_back(u);
}
dfs(1,0);
T=n;
fprintf(fw, "%d\n", T);
for(int i=1; i<=T; ++i){
fprintf(fw, "%d %d\n", i, rand(0,dep[i]-1));
}
}
int main(){
char s[100];
for(int i=5; i<=5; ++i){
sprintf(s,"%d.in", i);
fw=fopen(s,"w");
fun();
fclose(fw);
}
}

