2021牛客多校第一场题解 H I J K
H Hash Function (https://ac.nowcoder.com/acm/contest/11166/H)
标签:卷积
题意:
对于给定的集合\(S=\{a_0,a_1,...,a_{n-1}\}\),找到最小的正整数\(x\),使得所有数对\(x\)取模的结果互不相同。
其中 \(1 \le n \le 500000, 0 \le a_i \le 5000000, a_i \ne a_j\)
解法:
事后诸葛亮,这题做法是卷积。
求出\(a_i\)之间的差都有哪些,然后这些差的因数都不能是x。筛掉这些因数后最小数就是\(x\)。
如何筛掉差的因数呢?可以看出\(a_i\)的范围不大,先枚举因数\(i\),再枚举倍数\(k\)即可,时间复杂度\(O(n/1+n/2+...+n/n)=O(nlogn)\)
如何求出所有差值呢?卷积。\(\{a_0,a_1,...,a_{n-1}\}\)和\(\{a_{1-n},a_{2-n},...,a_0\}\)用01序列表示(比如说,vis[i]=0集合中没有i,vis[i]=1表示集合中有i),求fft加速的卷积即可求出\(b_k=\sum_{i=0}^{n-1}a_i\times a_{k-i}\),时间复杂度\(O(nlogn)\)
这是我第一次写fft和卷积,因此留下模板供以后使用:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=500000;
const double Pi=acos(-1);
//fft complex struct
struct Complex{
double x, y;
Complex(double x=0, double y=0):x(x),y(y){}
Complex operator+(Complex b){ return Complex(x+b.x,y+b.y); }
Complex operator-(Complex b){ return Complex(x-b.x,y-b.y); }
Complex operator*(Complex b){ return Complex(x*b.x-y*b.y,x*b.y+y*b.x); }
};
//fft varity define
int n, m;
Complex a[N+10<<2], b[N+10<<2], c[N+10<<2];
int r[N+10<<2];
//fft by butterfly
void fft(Complex *cm, LL cnum, LL tag){
for(int i=0; i<cnum; ++i) if(i<r[i]) swap(cm[i],cm[r[i]]);
for(int mid=1; mid<cnum; mid<<=1){
Complex wk=Complex(cos(2*Pi/(2*mid)),tag*sin(2*Pi/(2*mid)));
for(int j=0; j<cnum; j+=2*mid){
Complex w(1,0);
for(int k=0; k<mid; ++k){
Complex buf=w*cm[j+k+mid];
cm[j+k+mid]=cm[j+k]-buf;
cm[j+k]=cm[j+k]+buf;
w=w*wk;
}
}
}
}
//problem
int an;
bool vis[N+N+20];
int main(){
cin>>an;
for(int i=1, u; i<=an; ++i){
scanf("%d", &u);
a[u].x=1;
b[N-u].x=1;
}
//fft butterfly generation
int dgt=1, bits=0;
while(dgt<=N+N) { dgt<<=1; bits++; }
for(int i=0; i<dgt; ++i) r[i]=(r[i>>1]>>1)|((i&1)<<(bits-1));
//fft
fft(a,dgt,1);
fft(b,dgt,1);
for(int i=0; i<=dgt; ++i){
c[i]=a[i]*b[i];
}
fft(c,dgt,-1);
//problem
for(int i=0; i<=N+N; ++i){
vis[i]=((int)(c[i].x/dgt+0.5))!=0;
}
for(int i=N; i<=N+N; ++i){
vis[i]|=vis[N+N-i];
}
for(int i=0; i<=N; ++i){
vis[i]=vis[i+N];
}
vis[N+1]=false;
for(int i=1; i<=N+1; ++i){
bool ok=true;
for(int j=i; j<=N+1&&ok; j+=i){
if(vis[j]) ok=false;
}
if(ok){
printf("%d\n", i);
break;
}
}
return 0;
}
I Increasing Subsequence(https://ac.nowcoder.com/acm/contest/11166/I)
标签:DP,DP优化
题意:给出\(1-n\)的一个排列,A和B轮流选数。在第一轮,A随机选一个数,B随机选一个大于它的数。在之后的每一轮,A和B选的数字大于前面选择的所有数字,且每个人选的数字必须比他之前选的数字位置靠后。当一个人无法选数时,游戏结束,求选择的数字数量的期望。
数据范围:\(1 \le n \le 5000\),答案对\(998244353\)取模。
解法:
本菜狗没有看懂官方题解的第一种做法,自己用的第二种做法写出来的。
首先题意描述非常别扭,但是可以想到一种更好的表示方式:把这个排列的数值作为下标,获得一个记录位置的数组,即用\(b[i]\)表示i这个数字的位置。这样的好处是,两人轮流选数,选择的数字一定在之前的数字的右边。
\(n\)的范围是\(5000\),时间限制是\(2s\),因此\(O(N^2)\)的时间复杂度几乎是确定的了。这很容易往DP的方向思考。
设\(f[i][j]\)表示A选择的数字是\(i\),B选择的数字是\(j\)时,还可以下多少步。若\(i>j\),说明下一步轮到B了;若\(i<j\),说明下一步该A选择了。
转移过程即是:
可以想到,\(f[i][j]=f[j][i]\)。
我们把\(i\)和\(j\)中较大的那个元素数值从大到小枚举,作为第一层循环;将\(i\)和\(j\)较小的值从大到小枚举作为第二层循环。这样决定了状态的枚举是\(O(N^2)\),如果状态转移是\(O(N)\)的话,将会超时。
现在考虑优化这一过程。平均值的计算方法可以是 “数值之和 除以 数量” ,这两个部分可以分开计算,用某种数据结构维护。求\(f[i][j]\)时,若\(i>j\)即接下来轮到B了,那么需要用到\(f[i][k]\),此时三者关系为\(j<i<k\),也就是接下来\(j\)的循环(从\(i-1\)到\(1\))与\(k\)无关,因此这里可以预处理。可以用类似“前缀和”的方式,每一层外循环后,通过\(O(N)\)的预处理,使得之后的转移过程为\(O(1)\)。
实际上我一开始用的树状数组优化转移过程,转移过程是\(O(logN)\)的,算法总复杂度\(O(N^2logN)\),运行时间\(1.2s\)。后来看了题解才想到,直接前缀和\(O(1)\)转移不就ok了,总复杂度\(O(N^2)\),运行时间\(400ms\)。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL P=998244353;
const int N=5010;
LL power(LL a, LL p){
if(p==0) return 1;
if(p==1) return a;
LL tmp=power(a,p>>1);
if(p&1) return tmp*tmp%P*a%P;
return tmp*tmp%P;
}
LL f[N][N], inv[N];
int n;
int a[N], b[N];
LL tcnt[N][N], tsum[N][N], tcs[N], tss[N];
int main(){
//输入数据
cin>>n;
for(int i=1; i<=n; ++i){
scanf("%d", a+i);
b[a[i]]=i;
}
//预处理逆元
for(int i=1; i<=n; ++i){
inv[i]=power(i,P-2);
}
//求f
for(int i=1; i<n; ++i) f[i][n]=f[n][i]=1;
for(int i=n-1; i>=1; --i){
//预处理前缀和 tss->temporary sum sum(数值前缀和); tcs->temporary count sum(数量前缀和)
for(int j=1; j<=n; ++j) tss[j]=tcs[j]=0;
for(int j=i+1; j<=n; ++j){
tss[b[j]]=f[i][j];
tcs[b[j]]=1;
}
for(int j=1; j<=n; ++j){
tss[j]+=tss[j-1]; if(tss[j]>=P) tss[j]-=P;
tcs[j]+=tcs[j-1];
}
//转移过程
for(int j=i-1; j>=1; --j){
if(tcs[n]-tcs[b[j]]==0){
f[i][j]=f[j][i]=1;
continue;
}
f[i][j]=f[j][i]=((tss[n]-tss[b[j]]+P)*inv[tcs[n]-tcs[b[j]]]%P+1)%P;
}
}
//枚举第一轮的情况
LL res=0, sum, cnt;
for(int i=1; i<=n; ++i){
sum=cnt=0;
for(int j=1; j<=n; ++j){
if(a[j]>a[i]){
sum+=f[a[i]][a[j]];
cnt++;
}
}
if(!cnt) continue;
sum%=P;
res+=inv[cnt]*sum%P;
}
res=res%P*inv[n]%P;
res=(res+1)%P;
cout<<res<<endl;
}
J Journey among Railway Stations(https://ac.nowcoder.com/acm/contest/11166/J)
标签:线段树
题意:有一条列车路线,这条路线上共有\(n\)个车站,每个车站都有一个开门时间,如第i个车站开门时间为\(u_i \sim v_i\),只有在这段时间内列车才能停靠。相邻车站之间有距离,如第\(i\)个车站到第\(j\)个车站之间需要行驶的时间为\(cost_i\)。现在有\(Q\)个操作,每个操作是下面三类中的一种:
操作一:\("0\ l\ r"\) 列车从第\(l\)个车站,在\(u_l\)时刻出发,能否到达第\(r\)个车站,且在\([l,r]\)内的各个车站都停靠(停靠和启动、减速的时间不计)
操作二:\("1\ i\ w"\) 将第\(i\)个车站和第\(i+1\)个车站之间的路程改为\(w\)
操作三:\("2\ i\ p\ q"\) 将第\(i\)个车站的开门时间改为\(p \sim q\)
\(2 \le n \le 10^6 \ , \ 1 \le u_i \le v_i \le 10^9 \ , 1 \le l \le r \le n \ , \ 1 \le i \le n \ , \ 1 \le Q \le 10^6\), 输入的所有数字不超过\(10^9\)。
解法:
看这标准的数据范围,这么套路的三种操作,“复杂度\(O(NlogN)\)的数据结构”这几个字几乎已经打在了我们眼前。但是,即便如此也并不简单,这道题稀少的AC数时刻提醒着我们这一点。
这道题也有两种解法,我们先看解法一。
解法一:
我们设法列出数学表达式。令\(w[i]=cost_i\)对于l到r的区间,能在各个车站停车的条件是
设\(sum[i]=\sum_{i=1}^iw[i]\),我们用前缀和的方式改写:
可以看出\(u_i-sum[i-1]\)和\(v_i-sum[i-1]\)的特殊性。令\(U_i=u_i-sum[i-1],\ V_i=v_i-sum[i-1]\),我们只需要靠区间最大的\(U\)和最小的\(V\)的辅助,就能够推出一个区间是否满足要求。
对于一个区间\([l,r]\),令\(mid=(l+r)/2\),区间满足要求的条件是:\([l,mid]\)满足条件,\([mid+1,r]\)满足条件,且\([l,mid]\)中的最大的\(U\)不大于\([mid+1,r]\)中的最小的\(V\)。用线段树就可以处理了。
解法二:
我们设法感性地认识这个问题。对于一个车站,我们以到站时间为横轴,以出站时间为纵轴,画出曲线图。它长这个样子:
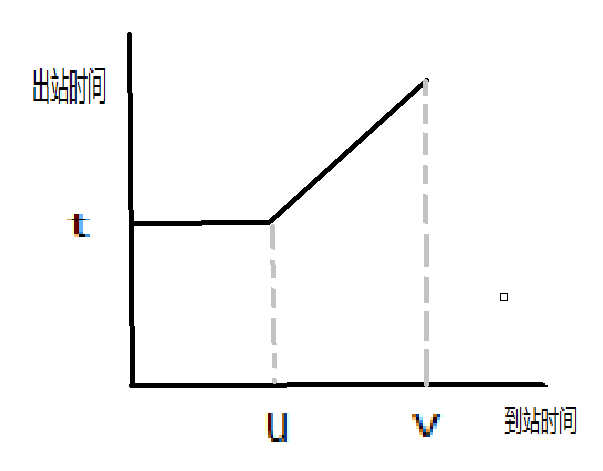
在\(u\)之前到车站的话,列车必须等到\(u\)时刻才能进站;在\(u、v\)之间到车站的话,可以立即出站;在\(v\)时刻之后就不能停靠了。想确定这个曲线的话只需要三个参数\((t,u,v)\)。
神奇的地方在于,如果我们将相邻的两个车站合并,会发现他们的曲线也是这个样子。因此可以用线段树维护这条曲线。区间\([l,r]\)存在这条曲线,当且仅当\([l,mid]\)存在曲线,\([mid+1,r]\)存在曲线,然后将这两个曲线合并即可,依然可以用线段树来做。
这道题我做得相当不好,先是思路想错了,WA了几发。后来沿着解法一的思路,推出了上面的式子,但是不会用线段树维护,只得以失败告终。最后我看了题解,按照解法一做了出来,但是代码写得相当丑,别人看了肯定会骂。之后看了题解,才恍然大悟原来线段树可以这么写。不得不承认我线段树的题目做得很少,这次算是补回来了一点了吧。
在此贴上两份代码。第一份是解法一我的代码,相当丑,主要丑在query函数里;第二份是解法二的std里令我佩服的merge函数和query函数。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=1e6+10;
struct Node{
LL v, u;
bool ok;
}nd[N<<2];
int n;
LL w[N], u[N], v[N];
LL sum[N];
LL lazy[N<<2];
//segment tree
#define lc (rt<<1)
#define rc (rt<<1|1)
#define mid (l+r>>1)
void pushdown(int rt){
lazy[lc]+=lazy[rt];
lazy[rc]+=lazy[rt];
nd[rt].v=min(nd[lc].v+lazy[lc],nd[rc].v+lazy[rc]);
nd[rt].u=max(nd[lc].u+lazy[lc],nd[rc].u+lazy[rc]);
lazy[rt]=0;
nd[rt].ok=nd[lc].ok&&nd[rc].ok&&(nd[lc].u+lazy[lc]<=nd[rc].v+lazy[rc]);
}
void build(int rt, int l, int r){
lazy[rt]=0;
if(l==r){
nd[rt].v=v[l]-sum[l-1];
nd[rt].u=u[l]-sum[l-1];
nd[rt].ok=true;
return;
}
build(lc,l,mid);
build(rc,mid+1,r);
pushdown(rt);
}
LL cquery_v(int rt, int l, int r, int L, int R){
if(l==L && r==R){
return nd[rt].v+lazy[rt];
}
if(R<=mid) return cquery_v(lc,l,mid,L,R)+lazy[rt];
if(L>mid) return cquery_v(rc,mid+1,r,L,R)+lazy[rt];
pushdown(rt);
return min(cquery_v(lc,l,mid,L,mid),cquery_v(rc,mid+1,r,mid+1,R));
}
LL cquery_u(int rt, int l, int r, int L, int R){
if(l==L && r==R){
return nd[rt].u+lazy[rt];
}
if(R<=mid) return cquery_u(lc,l,mid,L,R)+lazy[rt];
if(L>mid) return cquery_u(rc,mid+1,r,L,R)+lazy[rt];
pushdown(rt);
return max(cquery_u(lc,l,mid,L,mid),cquery_u(rc,mid+1,r,mid+1,R));
}
bool cquery(int rt, int l, int r, int L, int R){
if(l==L && r==R){
return nd[rt].ok;
}
if(R<=mid) return cquery(lc,l,mid,L,R);
if(L>mid) return cquery(rc,mid+1,r,L,R);
return cquery(lc,l,mid,L,mid) && cquery(rc,mid+1,r,mid+1,R) && (cquery_u(lc,l,mid,L,mid)<=cquery_v(rc,mid+1,r,mid+1,R));
}
void cupdata(int rt, int l, int r, int L, int R, int x){
if(l==L && r==R){
lazy[rt]+=x;
return;
}
if(R<=mid) cupdata(lc,l,mid,L,R,x);
else if(L>mid) cupdata(rc,mid+1,r,L,R,x);
else cupdata(lc,l,mid,L,mid,x), cupdata(rc,mid+1,r,mid+1,R,x);
pushdown(rt);
}
void cupdata_u(int rt, int l, int r, int L, int R, int x){
if(l==L && r==R){
nd[rt].u+=x;
return;
}
if(R<=mid) cupdata_u(lc,l,mid,L,R,x);
else if(L>mid) cupdata_u(rc,mid+1,r,L,R,x);
else cupdata_u(lc,l,mid,L,mid,x), cupdata_u(rc,mid+1,r,mid+1,R,x);
pushdown(rt);
}
void cupdata_v(int rt, int l, int r, int L, int R, int x){
if(l==L && r==R){
nd[rt].v+=x;
return;
}
if(R<=mid) cupdata_v(lc,l,mid,L,R,x);
else if(L>mid) cupdata_v(rc,mid+1,r,L,R,x);
else cupdata_v(lc,l,mid,L,mid,x), cupdata_v(rc,mid+1,r,mid+1,R,x);
pushdown(rt);
}
int main(){
freopen("02.in","r",stdin);
freopen("my.txt","w",stdout);
// cout<<N*11.5*8/1000/1000<<endl;
int T; cin>>T;
while(T--){
//input
scanf("%d", &n);
for(int i=1; i<=n; ++i) scanf("%lld", u+i);
for(int i=1; i<=n; ++i) scanf("%lld", v+i);
for(int i=1; i<n; ++i) scanf("%lld", w+i);
//init
for(int i=1; i<n; ++i) sum[i]=sum[i-1]+w[i];
build(1,1,n);
//query
int m, opt, l, r, x;
scanf("%d", &m);
while(m--){
scanf("%d", &opt);
switch(opt){
case 0:
scanf("%d%d", &l, &r);
puts(cquery(1,1,n,l,r)?"Yes":"No");
break;
case 1:
scanf("%d%d", &l, &x);
cupdata(1,1,n,l+1,n,w[l]-x);
w[l]=x;
break;
case 2:
scanf("%d%d%d", &x, &l, &r);
cupdata_v(1,1,n,x,x,r-v[x]);
cupdata_u(1,1,n,x,x,l-u[x]);
u[x]=l; v[x]=r;
break;
}
}
}
}
下面是std的神奇代码
//Function是线段树结点的结构体类型,含{valid,t,l,r}
Function Merge(const Function &A, const Function &B, int d){
if (!A.valid || !B.valid || A.t + d > B.r) return Function();
//if (A.t + d + A.r - A.l <= B.l) return Function(A.r, A.r, B.t);
LL newr = A.t + d + A.r - A.l > B.r ? B.r + A.l - A.t - d : A.r, newl, newt;
if (A.t + d >= B.l) newl = A.l, newt = B.t + A.t + d - B.l;
else newl = min(newr, A.l + B.l - A.t - d), newt = B.t;
return Function(newl, newr, newt);
}
void Query(int x, int l, int r, int ql, int qr){
if (ql <= l && r <= qr){
if (ql == l) ans = a[x]; else ans = Merge(ans, a[x], dist[l-1]);
return;
}
int mid = (l + r) >> 1;
if (ql <= mid) Query(x << 1, l, mid, ql, qr);
if (qr > mid) Query(x << 1 | 1, mid + 1, r, ql, qr);
}
K Knowledge Test about Match(https://ac.nowcoder.com/acm/contest/11166/K)
标签:贪心,乱搞,KM对拍
题意:有一个数组\(\{ b_0,\ b_2,\ ......,\ b_{n-1}\}\),每个数字是\(0\sim n-1\)等概率随机生成的。现在你可以给这个数组重新排序,使得\(\sum_{i=0}^{n-1} \sqrt{|b_i-i|}\)最小。共\(T\)组数据。设每组数据正确答案为\(f\),你的答案为\(g\),要求满足$$\frac{1}{T}\sum\frac{g-f}{f}<0.04$$
\(100 \le T \le 500 , \ 1 \le n \le 1000\)
解法:
这道题很怪,因为数据完全随机生成,而且答案允许误差。其实出题人的想法就是让同学们发挥自己的想象力乱搞,再用KM验证误差是否允许。
KM是带权的二分图最大匹配算法,时间复杂度\(O(N^3)\)。数组\(b_i\)如果放到了第\(j\)个位置上,相当于二分图的左部第\(i\)个点和右部第\(j\)个点连了一条权值为\(\sqrt{|b_i-i|}\)的边。我们可以建立一个\(2n\)个点,\(n^2\)条边的二分图,再求一个完备匹配使得权值和最小即可。
由于出题人数据范围设置的很巧妙,KM运行时间大概10几秒,交上去一定会T,但可以用来验证。因此同学们只能想方设法乱搞。
下面有两种乱搞方法。
方法一:先让\(|b_i-i|=0\)的尽可能多,再让\(|b_i-i|=1\)的尽可能多,以此类推。
方法二:玄学的交换方法。一次solve不够,写三次solve就能ac了。
double cal(int a, int b){
return sqrt(abs(a-b));
}
void solve(){
for(int i=0; i<n; ++i){
for(int j=i+1; j<n; ++j){
if(cal(a[i],i)+cal(a[j],j)>cal(a[i],j)+cal(a[j],i)) swap(a[i],a[j]);
}
}
}
下面附上KM验证的代码
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=1010;
const double INF=1e9, EXP=1e-7;
int n;
int a[N];
double e[N][N];
double lx[N], ly[N], slack[N];
int px[N], py[N], pre[N];
bool vx[N], vy[N];
queue<int> q;
void back(int v){
int t;
while(v){
t=px[pre[v]];
py[v]=pre[v];
px[pre[v]]=v;
v=t;
}
}
void km(int s){
//vx, vy, slack, q init
for(int i=1; i<=n; ++i) slack[i]=INF, vx[i]=vy[i]=false;
while(!q.empty()) q.pop();
q.push(s);
while(1){
while(!q.empty()){
int u=q.front(); q.pop();
vx[u]=true;
for(int i=1; i<=n; ++i) if(!vy[i]){
if(slack[i]>lx[u]+ly[i]-e[u][i]+EXP){//?=
slack[i]=lx[u]+ly[i]-e[u][i];
pre[i]=u;
if(slack[i]<EXP && slack[i]>-EXP){
vy[i]=true;
if(!py[i]){
back(i);
return;
}else{
q.push(py[i]);
}
}
}
}
}
double d=INF;
for(int i=1; i<=n; ++i) if(!vy[i]) d=min(d,slack[i]); //去掉vy[i],超时
for(int i=1; i<=n; ++i){
if(vx[i]) lx[i]-=d;
if(vy[i]) ly[i]+=d;
else slack[i]-=d;
}
for(int i=1; i<=n; ++i) if(!vy[i]){
if(fabs(slack[i])<EXP){
vy[i]=true;
if(!py[i]){
back(i);
return;
}else{
q.push(py[i]);
}
}
}
}
}
int main(){
int t; cin>>t;
while(t--){
scanf("%d", &n);
for(int i=1; i<=n; ++i){
scanf("%d", a+i);
}
//lx, ly init
for(int i=1; i<=n; ++i){
lx[i]=-INF; ly[i]=0;
}
//px py init
for(int i=1; i<=n; ++i){
px[i]=py[i]=0;
}
//e lx, ly init
for(int i=1; i<=n; ++i){
for(int j=1; j<=n; ++j){
e[i][j]=100.0-sqrt(fabs(a[i]-j+1));
lx[i]=max(lx[i],e[i][j]);
}
}
//km
for(int i=1; i<=n; ++i){
km(i);
}
// get ansf
double ans=-100*n;
for(int i=1; i<=n; ++i){
ans+=lx[i]+ly[i];
}
ans=-ans;
cout<<ans<<endl;
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号