2017 济南考前集训DAY2.AF
T1 洗澡
【问题描述】
你是能看到第一题的 friends 呢。 ——hja
洗澡的地方,有一段括号序列,将一个括号修改一次需要1的代价(将左括号变成右括号或者相反),求最小代价使得括号序列合法。
【输入格式】
一行一个括号序列。
【输出格式】
一行一个整数代表答案。
【样例输入】
())(
【样例输出】
2
【数据范围与规定】
对于50%的数据,括号序列长度不超过100。
对于100%的数据,括号序列长度不超过105且一定为偶数,只包含小括号。
思路 :水题 模拟

1 #include <cctype>
2 #include <cstdio>
3 #include <cstring>
4
5 const int MAXN=100010;
6
7 int len,top,cnt;
8
9 char s[MAXN];
10
11 int main(int argc,char**argv) {
12 freopen("shower.in","r",stdin);
13 freopen("shower.out","w",stdout);
14
15 scanf("%s",s+1);
16 len=strlen(s+1);
17 for(int i=1;i<=len;++i) {
18 if(s[i]=='(') ++top;
19 else if(s[i]==')'&&top) --top;
20 else ++cnt;
21 }
22 int ans=(top+1)/2+(cnt+1)/2;
23 printf("%d\n",ans);
24 return 0;
25 }
T2
日记
【问题描述】
你是能看到第二题的 friends 呢。 ——laekov
日记之中,写满了质数,两个质数之间如果没有其他质数,那么则称为相邻的质数。给定 , ,询问不超过 的数中能够表示成连续 个质数之和的最大的数是多少。
【输入格式】
第一行一个整数 代表数据组数。
对于每组数据,一行行两个整数。
【输出格式】
对于每组数据,一行一个整数代表答案。如果不存在,则输出−1。
【样例输入】
3
20 2
20 3
20 4
【样例输出】
18
15
17
【数据范围与规定】
对于20%的数据,1 ≤ ≤ 100。
对于40%的数据,T= 1。
对于另外20%的数据,所有的询问的N相等。
对于100%的数据,1 ≤T< 2000,1 ≤N≤ 106。
思路 :处理出所有1~1e6中的素数 求前缀和
每次二分查找满足要求的左区间的端点

1 #include <cctype>
2 #include <cstdio>
3 #define MAXN 1000010
4
5 typedef long long LL;
6
7 int tot,N,T,k;
8
9 int prime[80010];
10
11 LL sum[80010];
12
13 bool vis[MAXN];
14
15 inline void read(int&x) {
16 int f=1;register char c=getchar();
17 for(x=0;!isdigit(c);c=='-'&&(f=-1),c=getchar());
18 for(;isdigit(c);x=x*10+c-48,c=getchar());
19 x=x*f;
20 }
21
22 int main(int argc,char**argv) {
23 freopen("diary.in","r",stdin);
24 freopen("diary.out","w",stdout);
25
26 for(int i=2; i<MAXN; ++i) {
27 if(!vis[i]) prime[++tot]=i;
28 for(int j=1; j<=tot; ++j) {
29 if(i*prime[j] > MAXN) break;
30 vis[prime[j]*i]=true;
31 if(i%prime[j]==0) break;
32 }
33 }
34 for(int i=1; i<=tot; ++i) sum[i]=(LL)prime[i]+sum[i-1];
35
36 read(T);
37 while(T--) {
38 read(N);read(k);
39 int l=0,r=tot+1;
40 while(l+1<r) {
41 int mid=(l+r)>>1;
42 LL p=sum[mid+k-1]-sum[mid-1];
43 if(p<=N) l=mid;
44 else r=mid;
45 }
46 if(!l) printf("-1\n");
47 else printf("%lld\n",sum[l+k-1]-sum[l-1]);
48 }
49 return 0;
50 }
T3
洗衣
【问题描述】
你是能看到第三题的 friends 呢。 ——aoao
洗完衣服,就要晒在树上。但是这个世界并没有树,我们需要重新开始造树。
我们一开始拥有T0,是一棵只有一个点的树,我们要用它造出更多的树。
生成第 棵树我们需要五个参数Ai ,Bi ,Ci Di,Li , (Ai ,Bi < Li)。我们生成第i棵树是将第Ai棵树的Ci号点和第Bi棵树的Di号点用一条长度为Li的边连接起来形成的新的树(不会改变原来两棵树)。下面我们需要对新树中的点重编号:对于原来在第Ai棵树中的点,我们不会改变他们的编号;对于原来在第Bi棵树中的点,我们会将他们的编号加上第Ai棵树的点的个数作为新的编号。
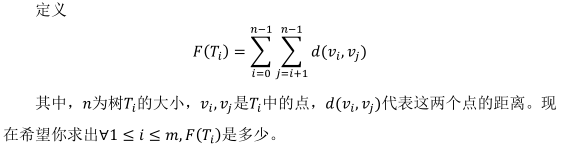


思路:大佬说是dp套dp (逃)
不妨设 g[i][j] 为第i颗树上的点到点j的距离
F[i] = F[a] + F[b] + siz[a] * siz[b] * Len[i] + g[a][c] * siz[b] +g[b][d] * siz[a]
对于 g[i][j]
我们不妨设 d[i][j][k] 为 在第 i 颗树上点j到点k的距离
假设 第 a 颗树 和第 b 颗树合并为第 t 颗树 有一条边连接 c 和 d
g[t][k] = g[b][d] + g[a][k] + (Len[i] + d[a][k][c] * siz[b])
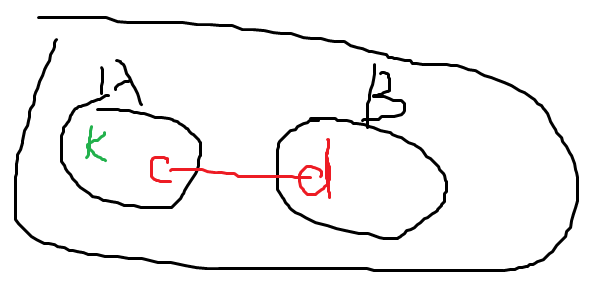
对于 d[i][j][k]
如果 本就在 第 i 颗树种中 那么 就查找 d[i][j][k]
如果 有一条边连接了 第 a 颗树 和 第 b 颗树
要求 d[t][p1][p2]
d[t][p1][p2] = d[a][p1][c] + d[b][p2][b] + Len[i]
由于状态过多 无法全部记录下来 因此我们进行记忆化搜索 用map保存每次搜到的状态
ps: 图片盗用的某大佬的
http://www.cnblogs.com/TheRoadToTheGold/p/7751264.html#_label2
作者:乌鸦坐飞机
出处:http://www.cnblogs.com/whistle13326/
新的风暴已经出现
怎么能够停止不前
穿越时空 竭尽全力
我会来到你身边
微笑面对危险
梦想成真不会遥远
鼓起勇气 坚定向前
奇迹一定会出现


