2017 济南考前集训DAY2.AM

 

T1

   

　　  

 

 

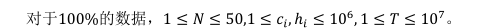
思路： 如果 楼高是有序的 

　　　 在任意的两个楼之间跳跃 楼高的花费是一定的。

　　　 比如 楼的高度 为 1 2 3 5 7

　　　 我们从 第1栋楼跳到第5栋楼的代价 和从第一栋楼 跳到第二栋楼再跳到第5栋楼的代价 是一样的

　　　 但是我们可以多跳一步

　　　 所以我们可以按照 楼的高度排序 

　　　 不妨设 dp[i][j] 为跳了i步 落在第j栋楼上 

　　　 转移 就枚举他是从哪一栋楼上跳过来的即可

 1 #include <cstdio>
 2 #include <cctype>
 3 #include <cstring>
 4 #include <algorithm>
 5 #define min(x,y) ((x) < (y) ? (x) : (y))
 6 
 7 const int MAXN = 55;
 8 
 9 int n,t;
10 
11 int dp[MAXN][MAXN];
12 
13 struct node {
14     int h,c;
15     friend inline bool operator < (node x,node y) {
16         return x.h<y.h;
17     }
18 };
19 node e[MAXN];
20 
21 inline void read(int&x) {
22     int f = 1;register char c = getchar();
23     for(x = 0;!isdigit(c);c == '-'&&(f = -1),c = getchar());
24     for(;isdigit(c);x = x * 10 + c - 48,c = getchar());
25     x = x * f;
26 }
27 
28 int main(int argc,char**argv) {
29     freopen("meet.in","r",stdin);
30     freopen("meet.out","w",stdout);
31     
32     read(n);
33     for(int i = 1; i <= n; ++i) read(e[i].c);
34     for(int i = 1; i <= n; ++i) read(e[i].h);
35     read(t);
36     
37     std::sort(e + 1,e + 1 + n);
38     memset(dp,63,sizeof dp);
39     for(int i = 1; i <= n; ++i) dp[0][i]=e[i].c;
40     for(int i = 1; i <= n; ++i) 
41       for(int j = 1; j <= n; ++j) {
42             for(int k = 1; k < j; ++k) 
43               dp[i][j] = min(dp[i][j], dp[i-1][k] + e[j].h - e[k].h);
44           dp[i][j] += e[j].c;
45       }
46     
47     for(int i = n; i >= 0; --i) 
48       for(int j = 1; j <= n; ++j)
49         if(dp[i][j] <= t) {
50               printf("%d\n",i + 1);
51               return 0;
52           }
53     
54     return 0;
55 }
代码

 

T2

 

 

  

思路： 设给出的数 为 b1 b2 ..

　　　 我们要求 a1 a2 ..

　　　 我们知道 a1 + a2 == b1 

　　　　　　　　a1 + a3 == b2 

　　　 但是 a1 + a4 和 a2 + a3 哪一个更小我们不知道

　　　 所以我们可以令 a2 + a3 == x  就可以解的 a1 a2 a3 的值

　　　 在 b序列中删去 b1 b2 x  最小的数就是a4 

　　　 再把 a2 + a4  a3 + a4 删去 最小的就是a5 

 1 #include <cstdio>
 2 #include <cctype>
 3 #include <cstring>
 4 #include <algorithm>
 5 
 6 const int MAXN = 50000;
 7 
 8 int n,t,tot;
 9 
10 int a[MAXN],ans[310][310],re[310];
11 
12 bool used[MAXN];
13 
14 inline void read(int&x) {
15     int f = 1; register char c=getchar();
16     for(x = 0;!isdigit(c);c == '-'&&(f = -1),c = getchar());
17     for(;isdigit(c);x = x * 10 + c - 48,c = getchar());
18     x = x * f;
19 }
20 
21 void check(int x) {
22     if((a[1] + a[2] + a[x])&1) return;
23     re[2] = (a[1] - a[2] + a[x]) >> 1;
24     re[1] = a[1] - re[2];
25     re[3] = a[2] - re[1];
26     
27     memset(used,false,sizeof used);
28     used[1] = used[2] = used[x] = true;
29     int pos,r;
30     for(int i = 3,k = 4; i <= t; ++i) {
31         if(used[i]) continue;
32         re[k] = a[i] - re[1];
33         
34         for(int j = 1; j < k; ++j) {
35             r = re[j] + re[k];
36             pos = std::lower_bound(a + 1,a + 1 + t,r)-a;
37             if(a[pos] != r) return;
38             while(pos < t && used[pos] && a[pos] == r) ++pos;
39             if(a[pos] != r) return;
40             used[pos] = true;
41         }
42         ++k;
43     }
44     
45     ++tot;
46     for(int i = 1; i <= n; ++i) ans[tot][i] = re[i];
47 }
48 
49 int main(int argc,char**argv) {
50     freopen("city.in","r",stdin);
51     freopen("city.out","w",stdout);
52     
53     read(n);
54     t = n * (n - 1) / 2;
55     for(int i = 1; i <= t; ++i) read(a[i]);
56     
57     std::sort(a + 1,a + 1 + t);
58     for(int i = 3; i <= t; ++i) {
59         if(a[i] == a[i-1]) continue;
60         check(i);
61     }
62     
63     printf("%d\n",tot);
64     for(int i = 1; i <= tot; ++i)  {
65         for(int j = 1; j <= n; ++j)
66           printf("%d ",ans[i][j]);
67         printf("\n");
68     }
69     return 0;
70 }
代码

T3

 

思路：分块

　　　对与 100 以内的 p 

　　　预处理除所有 a[i] % p 

　　　把余数相同的扔进一个 vector 中

　　　每次查询 l~r 区间内的数时 二分找到 最小的左端点和做大的右端点 输出长度

　　　对于 大于 100 的 p

　　　我们发现 % p 为 v 的数最多会存在100 个

　　  应为 % p 为 v 的数 只能是 v, v + p ,v + 2p , v + 3p, v + 4p ....

　　　把每个数的位置记录在一个vector中 每次进行二分查找即可

 1 #include <vector>
 2 #include <cstdio>
 3 #include <cctype>
 4 #include <algorithm>
 5 
 6 const int MAXN = 100010;
 7 
 8 int n,m;
 9 
10 int a[MAXN];
11 
12 std::vector<int> v1[110][110],b[MAXN];
13 
14 inline void read(int&x) {
15     int f = 1; register char c = getchar();
16     for(x = 0;!isdigit(c);c == '-'&&(f = -1),c = getchar());
17     for(;isdigit(c); x = x * 10 + c - 48,c = getchar());
18     x = x * f;
19 }
20 
21 int main(int argc,char**argv) {
22     freopen("light.in","r",stdin);
23     freopen("light.out","w",stdout);
24     
25     read(n);read(m);
26     for(int i = 1; i <= n; ++i) read(a[i]),b[a[i]].push_back(i);
27     
28     for(int i = 1; i <= 100; ++i)
29       for(int j = 1; j <= n; ++j)
30         v1[i][a[j]%i].push_back(j); 
31     
32     int l,r,p,v;
33     for(int i = 1; i <= m; ++i) {
34         read(l);read(r);read(p);read(v);
35         if(p <= 100) {
36             std::vector<int>::iterator L = std::lower_bound(v1[p][v].begin(), v1[p][v].end(), l);
37             std::vector<int>::iterator R = std::upper_bound(v1[p][v].begin(), v1[p][v].end(), r);
38             printf("%d\n",R - L);
39         }
40         else {
41             int _l = v,ans = 0;
42             while(_l <= 10000) {
43                 std::vector<int>::iterator L = std::lower_bound(b[_l].begin(), b[_l].end(), l);
44                 std::vector<int>::iterator R = std::upper_bound(b[_l].begin(), b[_l].end(), r);
45                 ans += R - L;
46                 _l+=p;
47             }
48             printf("%d\n",ans);
49         }
50     }
51     
52     return 0;
53 }
代码

 

posted @ 2017-11-06 10:32  拿叉插猹哈  阅读(150)  评论(0)  编辑  收藏  举报