湖南集训DAY4

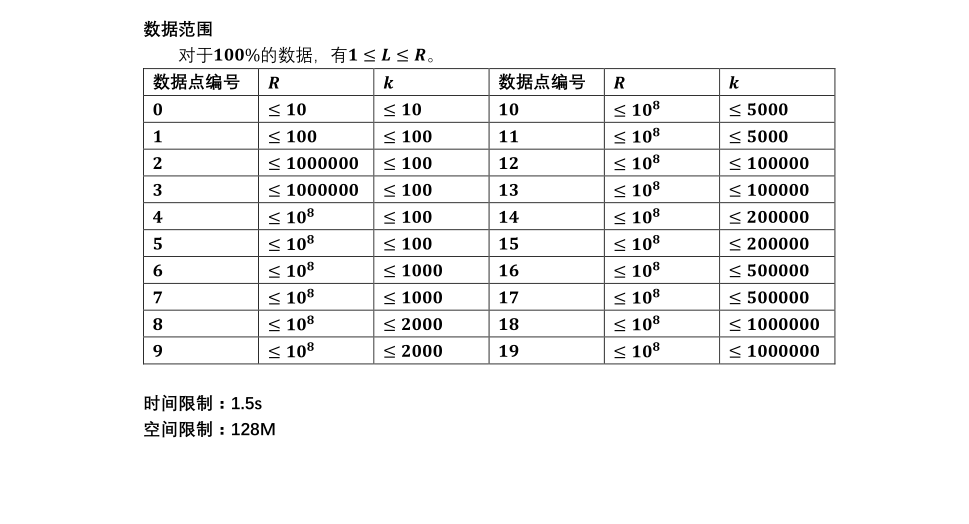
思路：打个表可以发现当 x>1 时 

　　　f(x) = x

　　　所以 题目就是求 ∑ i^k 

这个是需要用拉格朗日差值法求解

 

 

 1 #include <cstdio>
 2 const int Mod=998244353;
 3 const int MAXK=1000000;
 4 int power(int x,int k) {
 5     int ret=1;
 6     while (k) {
 7         if (k&1) ret=1LL*ret*x%Mod;
 8         x=1LL*x*x%Mod;
 9         k>>=1;
10     }
11     return ret;
12 }
13 int k;
14 int f[MAXK+10];
15 int pre[MAXK+10],suf[MAXK+10];
16 int jc[MAXK+10],K[MAXK+10];
17 int cnt(int n) {
18     if (n==0) return 0;
19     int ans=0;
20     if (n<=k+10 || n<=MAXK) {
21         for (int i=1; i<=n; i++) ans=(K[i]+ans)%Mod;
22     } else {
23         pre[0]=1;
24         for (int i=1; i<=k+2; i++) pre[i]=1LL*pre[i-1]*(n-i)%Mod;
25         suf[k+3]=1;
26         for (int i=k+2; i>=1; i--) suf[i]=1LL*suf[i+1]*(n-i)%Mod;
27         int l=k+1,r=0,flag=((k+1)&1)?(-1):(1);
28         for (int i=1; i<=k+2; i++) {
29             int s=1LL*pre[i-1]*suf[i+1]%Mod,m=1LL*(flag*jc[l]+Mod)*jc[r]%Mod;
30             ans=(1LL*f[i]*s%Mod*power(m,Mod-2)%Mod+ans)%Mod;
31             l--;
32             r++;
33             flag*=-1;
34         }
35     }
36     ans=((ans+K[2])%Mod-1+Mod)%Mod;
37     return ans;
38 }
39 int L,R;
40 void init() {
41     scanf("%d%d%d",&L,&R,&k);
42     for (int i=1; i<=MAXK+5; i++) K[i]=power(i,k);
43     jc[0]=1;
44     for (int i=1; i<=k+2; i++) jc[i]=1LL*jc[i-1]*i%Mod;
45     for (int i=1; i<=k+2; i++) f[i]=(f[i-1]+K[i])%Mod;
46     printf("%d\n",(cnt(R)-cnt(L-1)+Mod)%Mod);
47     return ;
48 }
49 int main() {
50     freopen("count.in","r",stdin);
51     freopen("count.out","w",stdout);
52     init();
53     fclose(stdin);
54     fclose(stdout);
55     return 0;
56 }
代码

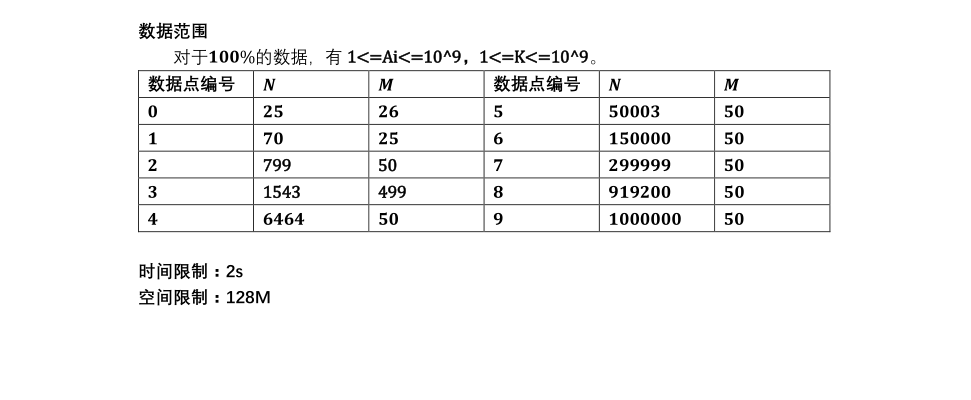
思路：每个数减去k，然后统计前缀和，维护两个指针，若选定区间内的区间和≥0，区间可行；

 1 #include <cstdio>
 2 #define ll long long
 3 #define Max(a,b) ((a)>(b)?(a):(b))
 4 const int MAXN=1000000;
 5 int n,m;
 6 int a[MAXN+10];
 7 ll sum[MAXN+10];
 8 int solve(int k) {
 9     static int st[MAXN+10];
10     int top=1,ret=0;
11     for (int i=1; i<=n; i++) {
12         sum[i]=sum[i-1]+a[i]-k;
13         if (!top || sum[i]<sum[st[top]]) st[++top]=i;
14     }
15     for (int i=n; i>=1; i--) {
16         while (top && sum[st[top]]<=sum[i]) top--;
17         ret=Max(ret,i-st[top+1]);
18     }
19     return ret;
20 }
21 void init() {
22     scanf("%d%d",&n,&m);
23     for (int i=1; i<=n; i++) scanf("%d",&a[i]);
24     for (int i=1; i<=m; i++){
25         int q;
26         scanf("%d",&q);
27         printf("%lld ",solve(q));
28     }
29     return ;
30 }
31 int main() {
32     freopen("blocks.in","r",stdin);
33     freopen("blocks.out","w",stdout);
34     init();
35     fclose(stdin);
36     fclose(stdout);
37     return 0;
38 }
代码

 

 

思路：求最长公共后缀 把字符数组翻转后就是最长的公共前缀了

　　　画一个trie树 发现最长公共前缀的长度就是 所有字符LCA的深度

 1 #include <cstdio>
 2 #include <cctype>
 3 #include <cstring>
 4 
 5 const int MAXN=1000010;
 6 const int MAXM=10010;
 7 
 8 int n,m,tot;
 9 
10 int t[MAXN][28],fa[MAXN][21],Len[MAXN],dep[MAXN];
11 
12 char s[MAXM];
13 
14 inline void read(int&x) {
15     int f=1;register char c=getchar();
16     for(x=0;!isdigit(c);c=='-'&&(f=-1),c=getchar());
17     for(;isdigit(c);x=x*10+c-48,c=getchar());
18     x=x*f;
19 }
20 
21 void build_Tree(int bj) {
22     int now=1;
23     int len=strlen(s+1);
24     
25     for(int i=len; i; --i) {
26         int x=s[i]-'a'+1;
27         if(!t[now][x]) {
28             t[now][x]=++tot;
29             dep[tot]=dep[now]+1;
30             fa[tot][0]=now;
31             for(int i=1; i<=20; ++i) fa[tot][i]=fa[fa[tot][i-1]][i-1];
32         }
33         now=t[now][x];
34     }
35     Len[bj]=now;
36 }
37 
38 int Query_LCA(int a,int b) {
39     if(dep[a]<dep[b]) a^=b^=a^=b;
40     for(int i=20;i>=0;--i) 
41       if(dep[fa[a][i]]>=dep[b]) a=fa[a][i];
42     if(a==b) return a;
43     for(int i=20;i>=0;--i) 
44       if(fa[a][i]!=fa[b][i])
45         a=fa[a][i],b=fa[b][i];
46     return fa[a][0];
47 }
48 
49 int hh() {
50     freopen("biology.in","r",stdin);
51     freopen("biology.out","w",stdout);
52     read(n);read(m);
53     tot=1,dep[0]=-1;
54     for(int i=1; i<=n; ++i) {
55         scanf("%s",s+1);
56         build_Tree(i);
57     }
58     
59     for(int flag,k,Lca,i=1; i<=m; ++i) {
60         read(flag);
61         if(flag==1) {
62             scanf("%s",s+1);
63             build_Tree(++n);
64         }
65         else {
66             read(k);
67             read(Lca);
68             Lca=Len[Lca];
69             for(int V,i=1; i<k; ++i) {
70                 read(V);
71                 Lca=Query_LCA(Lca,Len[V]);
72             }
73             printf("%d\n",dep[Lca]);
74         }
75     }
76     return 0;
77 }
78 
79 int sb=hh();
80 int main(int argc,char**argv) {;}
代码

 

posted @ 2017-10-19 14:28  拿叉插猹哈  阅读(156)  评论(0)  编辑  收藏  举报