洛谷 P1213 时钟 &&IOI 1994 The Clocks

                                                         IOI 1994 The Clocks

题目描述

考虑将如此安排在一个 3 x 3 行列中的九个时钟:

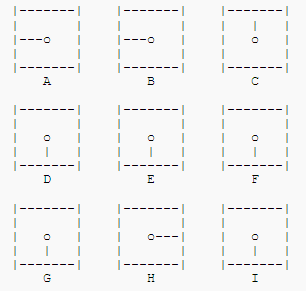
目标要找一个最小的移动顺序将所有的指针指向12点。下面原表格列出了9种不同的旋转指针的方法，每一种方法都叫一次移动。选择1到9号移动方法，将会使在表格中对应的时钟的指针顺时针旋转90度。

移动方法 受影响的时钟

1 ABDE

2 ABC

3 BCEF

4 ADG

5 BDEFH

6 CFI

7 DEGH

8 GHI

9 EFHI

Example

[但这可能不是正确的方法，请看下面]

输入输出格式

输入格式：

 

第1-3行: 三个空格分开的数字，每个数字表示一个时钟的初始时间，3,6,9,12。数字的含意和上面第一个例子一样。

 

输出格式：

 

单独的一行包括一个用空格分开的将所有指针指向12:00的最短移动顺序的列表。

如果有多种方案，输出那种使其连接起来数字最小的方案。(举例来说5 2 4 6 < 9 3 1 1)。

 

输入输出样例

输入样例#1：

9 9 12
6 6 6
6 3 6 

输出样例#1：

4 5 8 9

说明

题目翻译来自NOCOW。

USACO Training Section 1.4

 

暴力bfs 在vijos 上是可以A的

但是在洛谷 会被卡掉两个点  1.3s 死活没法再优化了

若有会的dalao 帮帮我 

 

换dfs 

每一种变换 最多变3次 第四次就回到原来的状态

所以我们可以dfs每一种变换方式的次数 最多三次 

bfs超时数据 dfs 0.1s毫无压力 

 

#include <queue>
#include <ctime>
#include <cstdio>
#include <cctype>
#include <cstring>
#include <algorithm>

/*int z[9][9]={{1,1,0,1,1,0,0,0,0},
			 {1,1,1,0,0,0,0,0,0},
			 {0,1,1,0,1,1,0,0,0},
			 {1,0,0,1,0,0,1,0,0},
			 {0,1,0,1,1,1,0,1,0},
			 {0,0,1,0,0,1,0,0,1},
			 {0,0,0,1,1,0,1,1,0},
			 {0,0,0,0,0,0,1,1,1},
			 {0,0,0,0,1,1,0,1,1},
			};*/

int z[10][10] = {{0},{1,2,4,5},{1,2,3},{2,3,5,6},{1,4,7},{2,4,5,6,8},
                  {3,6,9},{4,5,7,8},{7,8,9},{5,6,8,9}};

int s[10];

struct node {
	int s[10];
	int cnt;
	int path[100];
	friend bool operator < (node x,node y) {
		return x.cnt>y.cnt;
	}
};
node a,now,t;

bool f[4][4][4][4][4][4][4][4][4];

inline void read(int&x) {
	register char c=getchar();
	for(x=0;!isdigit(c);c=getchar());
	for(;isdigit(c);x=x*10+c-48,c=getchar());
}

inline bool pd(int*p) {
	for(int i=0;i<9;++i) if(p[i]) return false;
	return true;
}

inline bool check(int*p) {
	if(f[p[0]][p[1]][p[2]][p[3]][p[4]][p[5]][p[6]][p[7]][p[8]]) return false;
	f[p[0]][p[1]][p[2]][p[3]][p[4]][p[5]][p[6]][p[7]][p[8]]=1;
	return true; 
}

inline void BFS() {
	std::priority_queue<node> q;
	memcpy(a.s,s,sizeof s);
	q.push(a);
	while(!q.empty()) {
		now=q.top();
		q.pop();
		for(int i=1;i<=9;++i) {
			t=now;
			if(pd(now.s)) {
				std::sort(now.path+1,now.path+now.cnt+1);
				for(int k=1;k<=now.cnt;++k) printf("%d ",now.path[k]);
				return;
			}
			for(int j=0;z[i][j];++j) {
				++t.s[z[i][j]-1];
				if(t.s[z[i][j]-1]>=4) t.s[z[i][j]-1]-=4;
			}
			if(check(t.s)) {
				t.path[++t.cnt]=i;
				q.push(t);
			}	
		}
	}
	return;
}

int hh() {
	freopen("1.out","r",stdin);
	int t=clock();
	for(int x,i=0;i<9;++i)
	   read(x),x=(x/3)%4,s[i]=x;//
	f[s[0]][s[1]][s[2]][s[3]][s[4]][s[5]][s[6]][s[7]][s[8]]=1;
	BFS();
	printf("%d\n",clock());
	return 0;
}

int sb=hh();
int main(int argc,char**argv) {;}

　　

#include <queue>
#include <ctime>
#include <cstdio>
#include <cctype>
#include <cstring>
#include <algorithm>

const int MAXN=10;

int z[9][9]={{1,1,0,1,1,0,0,0,0},
			 {1,1,1,0,0,0,0,0,0},
			 {0,1,1,0,1,1,0,0,0},
			 {1,0,0,1,0,0,1,0,0},
			 {0,1,0,1,1,1,0,1,0},
			 {0,0,1,0,0,1,0,0,1},
			 {0,0,0,1,1,0,1,1,0},
			 {0,0,0,0,0,0,1,1,1},
			 {0,0,0,0,1,1,0,1,1},
			};

int s[MAXN],tmp[MAXN],ans[MAXN];

inline void read(int&x) {
	register char c=getchar();
	for(x=0;!isdigit(c);c=getchar());
	for(;isdigit(c);x=x*10+c-48,c=getchar());
}

inline bool check() {
	for(int i=0;i<9;++i) if(tmp[i]) return false;
	return true;
}

inline void print() {
	for(int i=0;i<9;++i)
	  for(int j=0;j<ans[i];++j)
	    printf("%d ",i+1);
	exit(0);
}

inline void DFS(int step) {
	memcpy(&tmp,&s,sizeof tmp);
	for(int i=0;i<9;++i)
	  for(int j=0;j<9;++j)
	    tmp[i]=(tmp[i]+z[j][i]*ans[j])%4;
	if(check()) {print();}
	if(step==9) return;
	for(int i=0;i<4;++i)
	  ans[step]=i,DFS(step+1);	  
	return;
}

int hh() {
//	freopen("1.out","r",stdin);
//	int t=clock();
	for(int x,i=0;i<9;++i)
	   read(x),x=(x/3)%4,s[i]=x;
	DFS(0);
//	printf("%d\n",clock());
	return 0;
}

int sb=hh();
int main(int argc,char**argv) {;}