[hdu 2089] 不要62 数位dp|dfs 入门

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=2089

题意：求[n, m]区间内不含4和62的数字个数。

这题有两种思路，直接数位dp和dfs

数位dp:

　　dp[i][j]表示i位数，首位是j的符合要求的数字个数。

　　j = 4时    dp[i][j] = 0

　　j != 4时

　　 

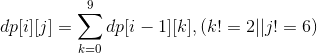
　　例如求dp[3][2]，2xx的个数，2已经确定了，2后面xx的个数即为2xx的个数，只用求出0x, 1x, 2x...9x的个数之和即可。同时要注意限制条件，dp[i][4]均为0，如果i位首位为6，i-1位首位为2的话也为0。这样我们首先预处理下，然后由此可以求区间内所符合要求的数字个数。

　　以求[0, 365]为例，先求0xx, 1xx, 2xx, xx的个数即为每个的个数，当然如果是555的的话4xx是跳过的，或者前一位是6，那么2xx也要跳过。然后求[300, 365]的个数，已经确定首位为3，求3xx的个数，然后类似的确定xx的个数。如果遇到456这种情况，只用求0xx,1xx,2xx,3xx的个数，4xx就不用求了，因此最外层循环就可以停止了。类似的6223.. 没必要求[6200,6223]了。

代码：

#include <iostream>
#include <stdio.h>
#include <cstring>
#include <algorithm>
using namespace std;

int dp[10][10];
int d[10];

void init()
{
    memset(dp, 0, sizeof(dp));
    dp[0][0] = 1;
    for(int i = 1; i <= 7; i++)
        for (int j = 0; j <= 9; j++)
            for (int k = 0; k <= 9; k++)
                if (j != 4 && !(j==6 && k==2))
                    dp[i][j] += dp[i-1][k];
}

int solve(int n)
{
    int ans = 0, len = 0;
    while (n) {
        d[++len] = n % 10;
        n /= 10;
    }
    d[len+1] = 0;
    for (int i = len; i >= 1; i--) {
        for (int j = 0; j < d[i]; j++) {
            if (d[i+1] != 6 || j != 2)
                ans += dp[i][j];
        }
        if (d[i]==4 || (d[i+1]==6 && d[i]==2))
            break;
    }
    return ans;
}


int main()
{
    freopen("1.txt", "r", stdin);
    int n, m;
    init();
    while (~scanf("%d%d", &n, &m)) {
        if (n + m == 0) break;
        printf("%d\n", solve(m+1)-solve(n));
    }


    return 0;
}

DFS+记忆化搜索:

　　dp[i][j]表示i位数，前一位数组是否为6的符合要求的个数。

　　dfs的参数l是当前的位数，从最高位开始搜索。six是前一位是否为6，limit是最高位是否受限，如365，最高位就受限与0~3，然后开始搜索0xx, 1xx, 2xx, 3xx, 其中0xx,1xx,2xx中的xx都是不受限的，0~99均可取，而3xx中的xx要受65的限制，搜索下一位时继续设限。如果该位为4，或上一位为6，该位为2时就跳过不搜。另外搜索中有大量重复，所以采用记忆化搜索。如果受限的话就不能采用记忆化搜索的结果。

代码：

 

#include <iostream>
#include <stdio.h>
#include <cstring>
#include <algorithm>
using namespace std;

int digit[10], dp[10][2], v[10][2];

int dfs(int l, bool six, bool limit)
{
    if (l == 0) return 1;
    if (!limit && v[l][six]) return dp[l][six];
    int len = limit ? digit[l] : 9;
    int nx = 0;
    for (int i = 0; i <= len; i++) {
        if ((i == 4) || (six&&i==2))
            continue;
        nx += dfs(l-1, i==6, limit&&(i==len));
    }
    if (!limit) {
        v[l][six] = true;
        dp[l][six] = nx;
    }
    return nx;
}

int sum(int n)
{
    memset(dp, 0, sizeof(dp));
    memset(v, 0, sizeof(v));
    int pos = 0;
    while (n) {
        digit[++pos] = n % 10;
        n /= 10;
    }
    int ans = dfs(pos, false, true);
    return ans;
}
int main()
{
    //freopen("1.txt", "r", stdin);
    int n, m;
    while (~scanf("%d%d", &n, &m)) {
        if (n + m == 0) break;
        printf("%d\n", sum(m)-sum(n-1));
    }

    return 0;
}

 

ps:注意两者在[n, m]时的处理。