逻辑回归

对于特征\(x=(x_1,x_2,..,x_d)\)来说，我们可以计算器加权“风险分数”$$s=\sum_{i=0}^d w_ix_i$$
但这是一个实数领域的数值，我们想把其映射到0到1之间来表示不同类别的概率，则可使用下面sigmoid函数：

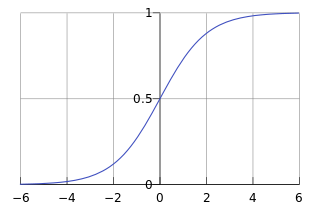
sigmoid函数公式是\(\theta(x)=\frac{1}{1+e^{-x}}\)，把\(w^Tx\)带入得\(f(x)=\frac{1}{1+e^{-w^Tx}}\)

知道了函数形式，下面要求逻辑回归函数的损失函数，我们的函数等价于\(f(x)=P(+1|x)\)。假设我们的数据集为\(D=\{(x_1,-1),(x_2,1),...,(x_N,1)\}\),那么这个数据集出现的几率是\(P(x_1)P(-1|x_1)P(x_2)P(1|x_2)...P(x_N)P(1|X_N)\),那么f(x)产生这样一个数据集的可能性为 \(P(x_1)h(x_1)P(x_2)(1-h(x_2))...P(x_N)(1-h(x_N))\),如果h和f是相近的，那么h对数据集的概率应该和f是相近的，而由于f的数据集是已经出现的，那么根据大数定律则可认为f产生的数据集概率是比较大的。

那么，最大化

\[likelihood(h)=P(x_1)h(x_1)P(x_2)(1-h(x_2))...P(x_N)(1-h(x_N)) =h(x_1)h(-x_2)...h(-x_N) =\prod_{n=1}h(y_nx_n) \]

等价于\(max_wlikelihood(w)=\prod_{n=1}^N\theta(y_nw^Tx_n)\)，两边同时取对数得\(max_wlog likelihood(w)=\sum_{n=0}^Nln\theta(w^Tx_ny_n)\),由于我们一直求的都是极小值，所以对其做个转化\(min_wlog likelihood(w)=\sum_{n=0}^N-ln\theta(w^Tx_ny_n)\)，由于\(\theta(s)=\frac{1}{1+exp^{(-s)}}\)，带入得$$min_w\frac{1}{N}\sum_{n=1}^{Nln(1+exp(-y_nw}Tx_n))$$,\(ln(1+exp(-y_nw^Tx_n))\)可被称作是逻辑回归的单点误差，即\(err(w,x,y) = ln(1+exp(-y_nw^Tx_n))\)。

我们的目标是要最小化误差函数，即\(min_wE_{in}(w)=\frac{1}{N}\sum_{n=1}^Nln(1+exp^{(-y_{nw^Tx_n})})\),对两边求导得：

\[\partial \]