数据结构(三) 用java实现七种排序算法。
很多时候,听别人在讨论快速排序,选择排序,冒泡排序等,都觉得很牛逼,心想,卧槽,排序也分那么多种,就觉得别人很牛逼呀,其实不然,当我们自己去了解学习后发现,并没有想象中那么难,今天就一起总结一下各种排序的实现原理并加以实现。
-WZY
一、文章编写风格总览
选择排序、插入排序、冒泡排序、归并排序、快速排序、希尔排序、堆排序、
最后对各种排序算法进行比较,理清楚各种排序的优缺点。
其中快速排序是冒泡排序的增强,堆排序是对选择排序的增强,希尔排序是对插入排序的增强,这就6种了,最后一种就是归并排序。
二、选择排序
选择排序是我认为最简单的一种排序了,因为我们自己也很容易想到这种方法对数组进行排序,原理非常简单,
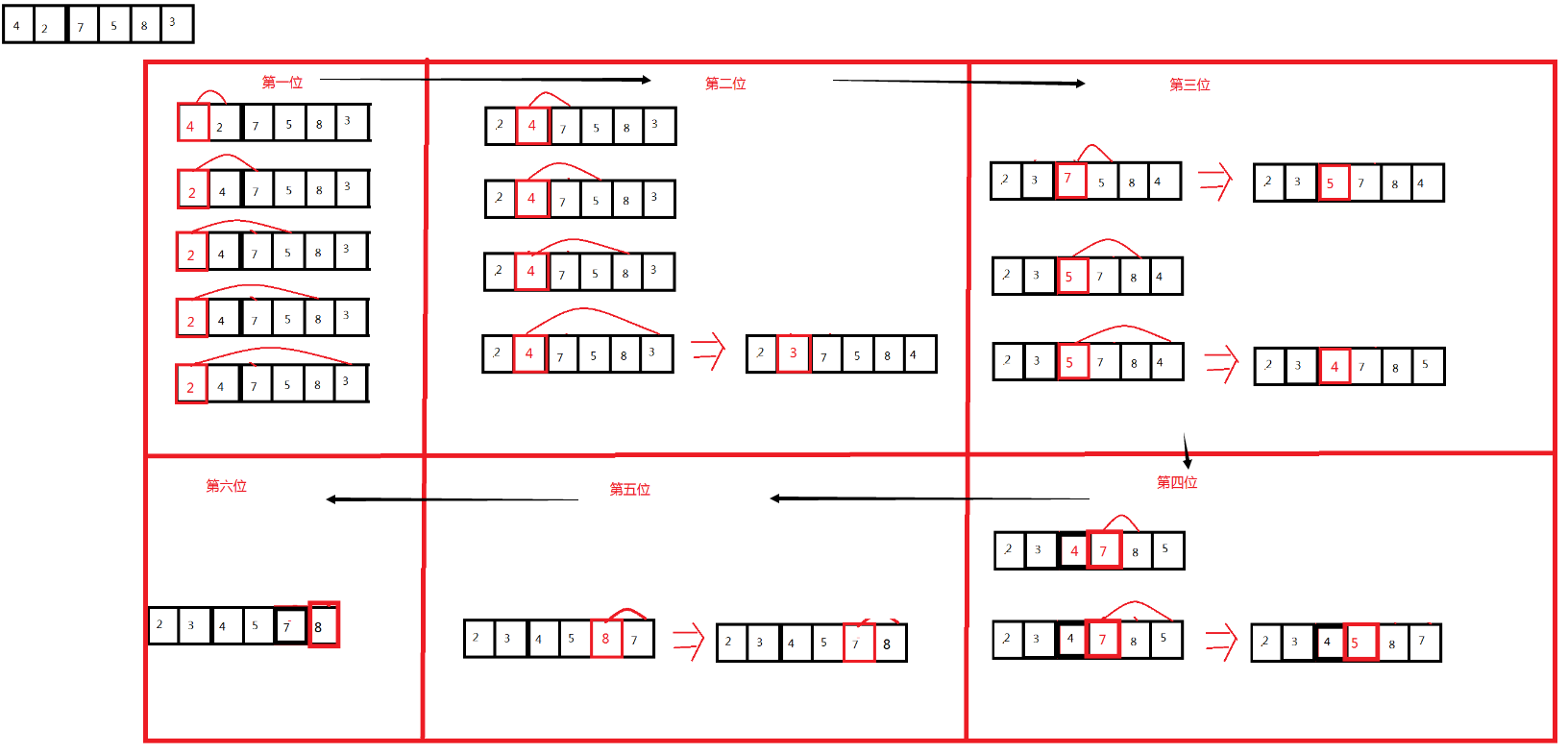
原理图如上所示:先将第一个位值上的数跟之后所有位置上的数依次进行比较,如果第一个位置上的数比第二个位置上的数大,则进行互换,然后继续将第一个位置上的数与第三个位置上的数进行比较,经过一轮的比较后,第一个位值上的数就是所有数中最小的一个,接着将第二个位置上的数与之后所有位置上的数进行比较,同样的规则,第二轮比较结束后,第二位放的就是所有数中第二小的数,依次往下比,直到最后一个位置结束。按照这种方法进行排序,就叫做选择排序。
代码实现

测试


//选择排序,将数组按从小到大排序 public void selectSort(int[] array){ //根据原理分析,使用两层循环即可实现 for(int i=0; i<array.length; i++){//第一层 for(int j=i+1; j<array.length;j++){ //第二层 if(array[i] > array[j]){ //数据互换。将小的放前面 int t = array[i]; array[i] = array[j]; array[j] = t; } } } }
舞蹈:http://v.youku.com/v_show/id_XMjU4NTY5NTcy.html
三、插入排序
简单,给定的一组记录,将其分为两个序列组,一个为有序序列(按照顺序从小到大或者从大到小),一个为无序序列,初始时,将记录中的第一个数当成有序序列组中的一个数据,剩下其他所有数都当做是无序序列组中的数据。然后从无序序列组中的数据中(也就是从记录中的第二个数据开始)依次与有序序列中的记录进行比较,然后插入到有序序列组中合适的位置,直到无序序列组中的最后一个数据插入到有序序列组中为止。
原理图

代码实现
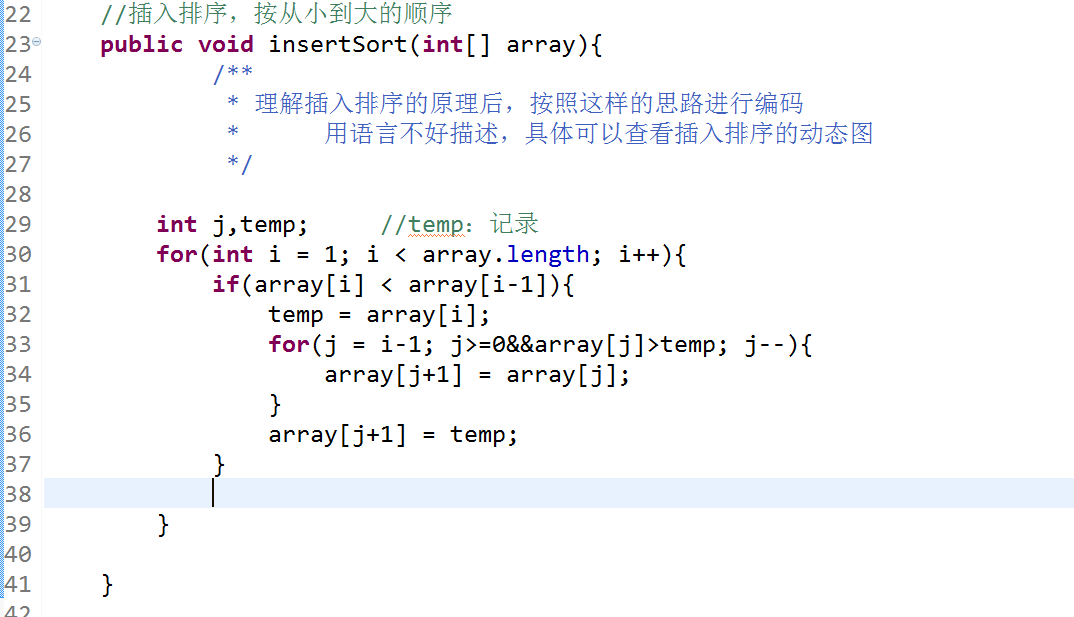

//插入排序,按从小到大的顺序 public void insertSort(int[] array){ /** * 理解插入排序的原理后,按照这样的思路进行编码 * 用语言不好描述,具体可以查看插入排序的动态图 */ int j,temp; //temp:记录 for(int i = 1; i < array.length; i++){ if(array[i] < array[i-1]){ temp = array[i]; for(j = i-1; j>=0&&array[j]>temp; j--){ array[j+1] = array[j]; } array[j+1] = temp; } } }
很有趣的视频,插入排序的趣味舞蹈:http://v.youku.com/v_show/id_XMjU4NTY5MzEy.html
四、冒泡排序
冒泡排序跟选择排序一样的简单,好理解,整个过程就想气泡一样往上升,假设从小到大排序,对于给定的n个记录,从第一个记录开始依次对相邻的两个记录进行比较,当前面的记录大于后面的记录时,交换位置,进行一轮比较后,第n位上就是整个记录中最大的数,然后在对前n-1个记录进行第二轮比较,重复该过程直到进行比较的记录只剩下一个为止。

代码实现


//冒泡排序,从小到大 /** * 通过看冒泡排序的原理图,我们知道只要让其一直遍历数组即可,只不过每遍历一次,就要让遍历的长度减1, * 所有就在遍历的外面加一层while循环。判断的条件为,当遍历的长度>=1时,此时就只需要遍历两个数据了,比完后不应该在继续。 * 非常简单的逻辑。 * * @param array */ public void bubbleSort(int[] array){ int j = array.length - 1; while( j >= 1){ for(int i = 0; i < j; i++){ if(array[i] > array[i+1]){ int t = array[i]; array[i] = array[i+1]; array[i+1] = t; } } j--; } }
冒泡排序:http://v.youku.com/v_show/id_XMzMyOTAyMzQ0.html
五、归并排序
归并排序有两种实现方式,一种是非递归的,一种是递归的,但是我觉得如果你理解了非递归的实现,那么你就知道了归并排序的原理,而递归的也就非常简单了。
什么是归并排序呢?(我们讲解的是2路归并排序)
一张图就可理解什么叫做2路归并排序

初始将一个数组中每个元素都看成一个有序序列(数组长度为n),然后将相邻两个有序序列合并成一个有序序列,第一趟归并就可以得到n/2个长度为2(最后一个有序序列的长度可能是1,也可能不是,关键看数组中元素的个数了)的有序序列,在进行两两归并,得到n/4个长度为4的有序序列(最后一个的长度可能小于4)...一直这样归并下去,直到得到一个长度为n的有序序列1
简单来说,通过三步,解决三个问题,就可以写出归并排序
1、解决相邻两个有序序列归并成一个有序序列,非常简单,新增一个数组(长度和需要排列的数组相同),
二路归并的核心操作,在归并的过程中,可能会破坏原来的有序序列,所以,将归并的结果存入另外一个数组中,设两个相邻的有序序列为r[s] ~r[m]和r[m+1]~r[t],将这两个有序序列归并成一个有序序列,r1[s]~r1[t],设三个参数i,j,k。 i和j分别指向两个有序序列的第一个记录,即i=s,j=m+1,k指向存放归并结果的位置(也就是将归并结果放到r1中的哪个位置)k=s。然后,比较i和j所指记录的数,取出较小者作为归并结果存入k所指的位置,然后将较小者的指向往后移动,直至两个有序序列之一的所有记录都取完,在将另一个有序序列的剩余记录顺序送到归并后的有序序列中(也就是放到r1中)


//一次归并 /** * 相邻两个有序序列归并成一个有序序列的过程 * @param r 原数组,需要归并的数组 * @param r1 新数组,归并后的数组 * @param s 两个有序序列的第一个有序序列的第一个元素的下标 * @param m 两个有序序列的第一个有序序列的最后一个元素的下标 * @param t 两个有序序列的第二个有序序列的最后一个元素的下标 */ public void merge(int[] r, int[] r1, int s, int m, int t){ int i = s; //两个有序序列的第一个有序序列的第一个元素的下标 int j = m+1; //两个有序序列的第二个有序序列的第一个元素的下标 int k = s; //新数组中的指向 while(i <= m && j <= t){//两个有序序列都没有遍历完 if(r[i] < r[j]){ r1[k++] = r[i++]; }else{ r1[k++] = r[j++]; } } //当其中一个序列遍历完之后,将剩下那个序列加到新数组中,判断是哪一个序列没有遍历完 while(i <= m){ r1[k++] = r[i++]; } while(j<=t){ r1[k++] = r[j++]; } }
2、如何完成一趟归并?
这里就需要分情况了,三种情况,
假设每个有序序列中的元素个数为h(第一次归并的h=1),i=0,从第一个元素开始。归并每次取两个有序序列,那么跨度就是2h,问题就来了,只要知道长度为n(n为数组的最大下标值)的数组中有几个这样的两个有序序列,那么可以进行不同的操作了。
第一种情况:(i+2*h-1) <= n //比如,i=0,h=1时,(i+2*h-1)的意思就是指向了第一个两个有序序列的最后一个位置的下标值,用它来跟n(n为数组最大的下标值)比较,如果小于n,那么说明后面还有别的数,如果等于n,说明到结尾了,整个数组正好全是两个有序序列得,不会有多余数。那么就执行一次归并,将这两个有序序列归并,然后i加2h。如果还符合这个条件,继续归并,如果不符合,判断别的情况。
第二种情况:(i+h-1) < n //说明最后还有两个有序序列,但是最后一个有序序列的长度不是h,同样将其进行归并
第三种情况: (i+h-1) >= n //说明只剩下最后一个有序序列,则直接将其有序序列送到r1的相应位置。


/** * 一趟归并排序 * @param r 原数组,需要归并操作的数组 * @param r1 新数组,归并好的数组 * @param h 步长多少(有序序列中含有的元素个数) * @param n 数组长度(数组下标的最大值) */ public void mergePass(int[] r, int[] r1, int h, int n){ //判断根据步长能分成多个有序序列, int i = 0; while((i+2*h-1) <= n){//待归并的两个相邻有序序列的长度均为h,需要理解(i+2*h-1)的意思。 merge(r,r1,i,i+h-1,i+2*h-1);//需要注意一次归并需要的参数 i += 2*h; } if(i+h-1 < n){//说明最后还有两个序列,第一个序列长度为h,第二个序列长度小于h merge(r,r1,i,i+h-1,n); i += 2*h; }else{//剩下最后一个序列,长度并且小于或等于h,不用归并了,直接放入新数组中 for(; i<=n; i++){ r1[i] = r[i]; } } }
3、完成整个归并排序
前面我们解决了两个问题,一个是两个有序序列如何进行归并,一个是如何判断完成一趟归并过程。现在就需要解决如何控制二路归并的结束呢?也就是需要归并多少趟。
当步长等于n或者大于n时,说明只剩下一个有序序列了,那么即归并结束了。


//二分归并排序非递归算法 //n:数组最大下标 public void mergeSort(int[] r, int[] r1,int n){ int h = 1; //从1开始排序 while(h<n){ //直到h>=n才结束,也就步长小于n时都要进行归并 mergePass(r,r1,h,n); //一趟归并 h = 2*h; mergePass(r1,r,h,n);//因为经过一趟归并后,r1就变为了那个需要归并的数组,那么r就充当新数组,并且这也能够让排序好的数组放回到r数组中 h = 2*h; } }
六、快速排序
快速排序是对冒泡排序的增强,增强得点在于:冒泡排序中,记录的比较和移动是在相邻两个位置进行的,记录每次交换只能后移一个位置,因而总的比较次数和移动次数较多,而快排记录的比较和移动是从两端向中间进行的,较大的记录一次就能从前面移动到后面,较小的记录一次就能从后面移动到前面,这样就减少了比较次数和移动次数
快速排序原理:选取一个轴值(比较的基准),将待排序记录分为独立的两个部分,左侧记录都是小于或等于轴值,右侧记录都是大于或等于轴值,然后分别对左侧部分和右侧部分重复前面的过程,也就是左侧部分又选择一个轴值,又分为两个独立的部分,这就使用了递归了。到最后,整个序列就变得有序了。
问题:如何选择轴值?如何将序列变成左右两部分?
轴值的选择有三种:
1、选取序列的第一个位置上的记录
2、选择序列的中间位置上的记录
3、将序列第一个位置 和 中间位置 和 末尾位置上的记录进行比较,选择大小居中的记录,
如何将序列划分成左右两部分?
看图的执行流程,当一趟比较下来,轴值的左侧和右侧就被排好了,其中利用了first和end两个参数,一个从起点开始,一个从末尾开始,当两个相等时,就将序列中所有记录都遍历了一遍,第一次的比较次数是和选择排序第一次比较次数是一样的,但是之后就开始不一样了,因为在轴值的左侧的元素就不用跟轴值右侧的元素进行比较了,而选择排序还是跟所有的比。


递归调用


/* * 对序列划分为左右两个部分, * 轴值为数组第一个元素 * i,first:指向需要进行左右两侧排序的序列的第一个位置 * j,end:指向需要进行左右两侧排序的序列的最后一个位置 */ public int Partition(int[] array, int first, int end){ int i = first; int j = end; while(i < j){ //i和j会慢慢往中间靠,当i==j时,说明已经排好左右两侧的数据了,这里为什么不写i!=j作为条件呢?原因是有些情况是first>end,比如first=0,而end=-1, while(i<j&&array[i] < array[j]){//右侧进行扫描,array[i]是轴值 j--; //最后一个元素是大于轴值的,那么就不动,因为已经在其右边的,j--,往前移动一个位置 } if(i < j){ //这一步是当array[i] > array[j]。轴值的位置变为了j int temp = array[i]; array[i] = array[j]; array[j] = temp; i++; } while(i<j&&array[i] < array[j]){//左侧扫描,如果都比轴值小的话,i往后移动 i++; } if(i < j){ //当发现有比轴值大的数时,进行互换 int temp = array[i]; array[i] = array[j]; array[j] = temp; j--; } } return j; } public void quickSort(int[] array, int first, int end){ if(first < end){ int pivot = Partition(array,first,end); //返回轴值的位置, quickSort(array,first,pivot-1);//第一次排好后,pivot-1就是左侧最尾部的位置 quickSort(array,pivot+1,end); //pivot+1,右侧最开始的位置。 } }
快速排序:http://v.youku.com/v_show/id_XMzMyODk4NTQ4.html
七、希尔排序
希尔排序其实是插入排序的升级版本,本质上进行的也是插入排序的操作,但是希尔排序并不是把一组记录看成一个整体,而将整个记录分为了若干组记录,然后在对每组记录进行插入排序,
分组规则为如下所示:假设有 1 2 3 4 5 6 7 8 9 10 十个位置(每个位置上都会放数,这里忽略数,只讨论位置)。(省略了插入排序操作,只对如何分组进行讲解,而完整的希尔排序就是在每次分组完之后进行插入排序操作即可)
步长为:5、3、1
第一次分为5组记录(组数跟步长是一样的):1,6 、2,7、3,8、 4,9、 5,10 这五组记录,分别对这五组记录进行插入排序。
第二次分为3组记录:1,4,7,10、2,5,8、3,6,9 这三组记录,分别对这三组记录进行插入排序
第三次分为1组记录:1 2 3 4 5 6 7 8 9 10, 为这组记录进行插入排序,
而步长只要满足最后一次为1,并且是从大到小即可。一般使用(数组长度/2) 或者 (数组长度/3 +1) 来代表步长。
这样做的好处是:
将待排序的数组元素分成多组,每组中记录数相对较少
经过前几次的排序后,整个序列变为了“基本有序序列”,最后在对所有元素进行一次直接插入排序。
直接插入排序对基本有序和记录数少的序列的效率是非常高的,而希尔排序就是利用了这两点。
原理图
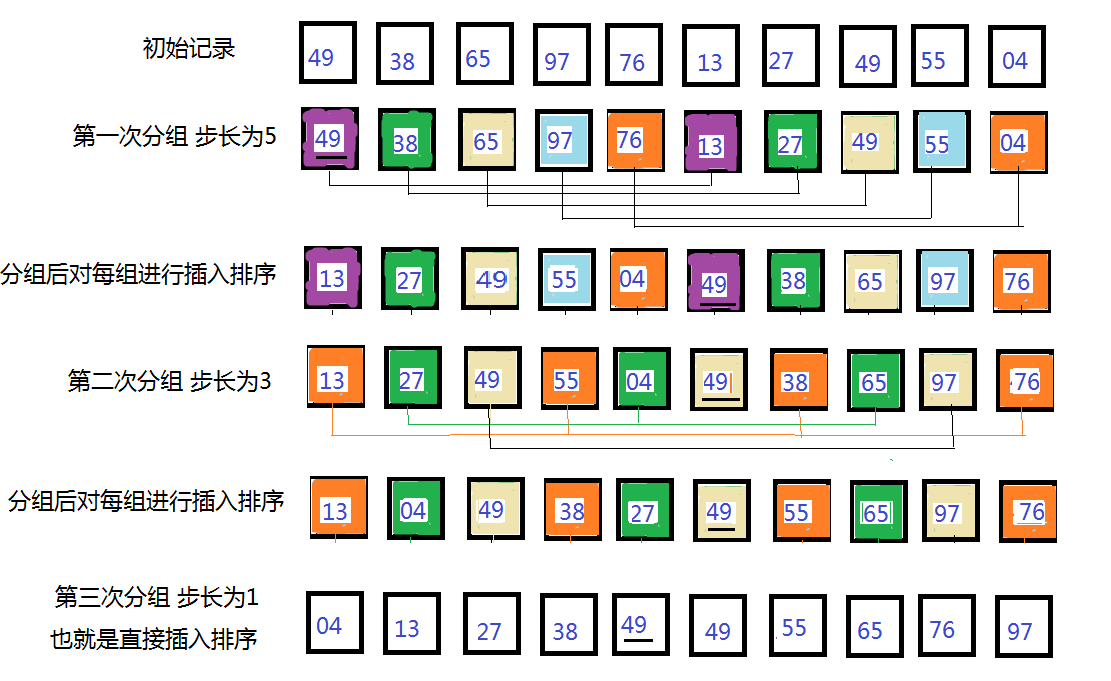
解释:第一次分组,49,13、38,27、65,49、97,55、76,04 五组,对这五组分别进行插入排序,在49找到13时,就会进行插入排序,位置会进行互换,而并非先全部分组,后排序。
按照步长一直重复执行,直到步长为1后,执行完最后一次直接插入排序,整个希尔排序就完成了。
运行时动态图:看最下面我分享的资源即可。(不知道博客园中如何上传.swf文件,或者动态图也不会如何上传。无奈)
代码实现


public void shellSort(int[] array){ int i,j,temp; //i,j分别为for循环中的控制变量 temp作用是临时记录数 int length = array.length; int gap = length; do{ gap = gap/2; //步长, 假设length为10,则步长为5 2 1 for(i = gap; i<length; i++){ if(array[i] < array[i-gap]){ temp = array[i]; for(j = i-gap; j>=0 && array[j]>temp; j-=gap){ array[j+gap] = array[j]; } array[j+gap] = temp; } } }while(gap>0); }
希尔排序舞蹈:http://v.youku.com/v_show/id_XMjU4NTcwMDIw.html
八、堆排序
上面说的希尔排序是对插入排序的增强,那么堆排序呢,就是对选择排序进行增强,选择排序一个数据要跟每个数据都进行一次比较,并没有利用到一些比较的结果,比如,4 跟10比较,3跟4比较后,按理说不用让3跟10在比了,但是选择排序并没有这种智能化,而是老老实实的比较,而堆排序就完美的利用了前几次比较的结果,从而增加了效率。
讲解堆排序之前,必须要知道什么是堆?
堆是一颗完全二叉树,什么是完全二叉树?只有最下面的两层结点度能够小于2,并且最下面一层的结点都集中在该层最左边的若干位置的二叉树(还不懂就去百度一下什么是完全二叉树)

这个图是一个完全二叉树,但不是堆。
堆分两种,大顶堆和小顶堆
大顶堆:在完全二叉树的基础上,每个父节点都比自己的两个子结点大,这样的就是大顶堆,特点是根节点是最大的值,看下图,90比70,80大,70比60,10大,以此类推

小顶堆:和大顶堆相反,根节点是最小的值,并且每个父结点都比自己的子节点要小,如下图
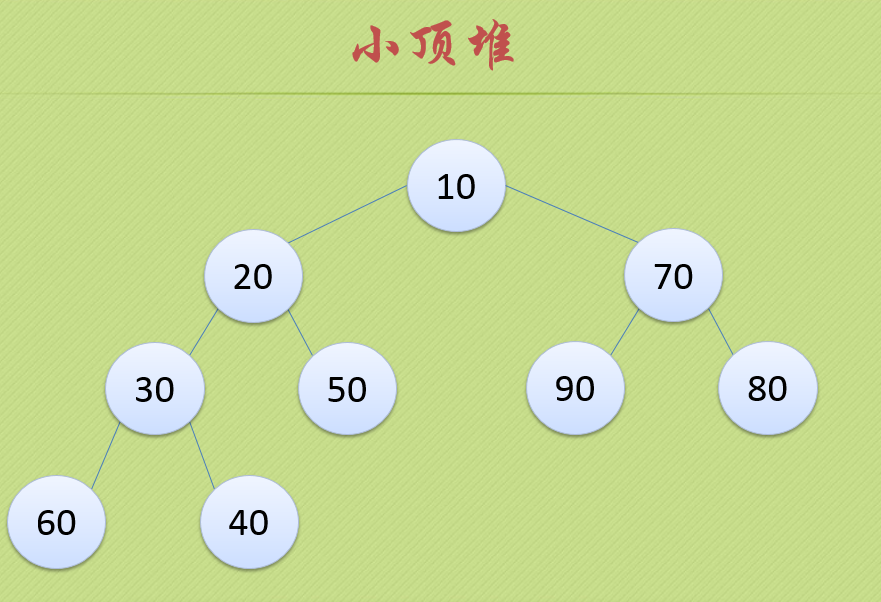
堆排序就是利用堆的这种特点进行编写的,原理:先将一组拥有n个元素的序列构建成大顶堆或者小顶堆,在将根结点上的数跟堆最后一位数进行互换,此时,第n位的数就是整个序列中最大或者最小的数了,然后在将前n-1位元素进行构建成大顶堆或者小顶堆,在将根结点跟第n-1位进行互换,得到第2大或者第2小的数,在将前n-2位数进行构建,依次类推,直到只剩下1位元素即结束,排序完成。
通过讲解原理:堆排序分为三步
1、构建大顶堆或小顶堆
2、循环
根节点和末尾结点进行互换,
构建大顶堆或小顶堆
3、排序完成



1 /* 2 * 要知道什么是堆这种数据结构 3 * 堆是一颗完全二叉树。分为大顶堆和小顶堆, 4 * 大顶堆,每个父结点都比自己的子节点大,也就是根结点为最大 5 * 小顶堆,每个父结点都比自己的子节点小,也就是根结点最小。 6 * 按照大顶堆和小顶堆这种特点,将一个无序的n个记录的序列构建成大顶堆,将根节点上的数与最后一个 7 * 结点n进行交换,然后在对n-1个记录进行构建大顶堆,继续把根节点与最后一个结点(n-1)互换,继续上面的操作。 8 * 从小到大排序,则使用大顶堆 9 * 从大到小排序,则使用小顶堆 10 * 从小到大 11 */ 12 public void heapSort(int[] array){ 13 //第一步:将数组构建成一个大顶堆 14 int length = array.length; //length为数组的长度,有几个数就是几,不要跟数组最大的下标值搞混淆了,有10个数,length就是10,数组最大下标为9 15 //找到完全二叉树中的最后一个父结点(拥有子结点)的位置length/2,也就是最后一个父节点是在完全二叉树的第length/2的位置上,但是在数组中的位置是 (length/2)-1,它代表父节点在数组中的位置 16 for(int i = length/2-1; i >= 0; i--){//依次遍历每一个父节点,比如最后一个父节点是4,那么它前面所有结点都是父节点,都需要进行构建 17 adjustMaxHeap(array,i,length); //无序序列,所以需要从下往上全部进行构建。该方法做的事情就是,比较找到父节点,和两个子节点中最大的数放置到父节点的位置上。 18 } 19 //第二步:构建好了大顶堆后,将第一个数与最后一个进行互换,互换后继续调整大顶堆, 20 for(int i = length-1; i > 0; i--){ 21 wrap(array, 0, i); //互换数据,提取出来了。互换数据后,就已经不在是大顶堆了,需要重新进行构建 22 adjustMaxHeap(array, 0, i); //从上往下,因为基本上都已经有序了,没必要在从下往上重新进行构建堆了,这就利用了前面比较的结果,减少了很多次比较。 23 } 24 } 25 26 //互换数据 27 private void wrap(int[] array, int i, int j){ 28 int temp = array[i]; 29 array[i] = array[j]; 30 array[j] = temp; 31 } 32 33 34 /** 35 * 构建大顶堆的操作, 36 * 父节点和其左右子节点的大小比较和互换,每次将父结点的位置和数组传进来, 37 * 就能构建出大顶堆了。 38 * 39 * @param array 排序数组 40 * @param s 当前所指父节点在数组中位置(下标) 41 * @param length 数组的长度。用来判断父节点的两个子节点是否存在。 42 * 父节点和左子结点的关系: 2s+1 43 * 父结点和右子结点的关系: 2s+2 44 */ 45 private void adjustMaxHeap(int[] array, int s, int length) { 46 int temp = array[s]; 47 int child; //代表更大一方的子节点的数组下标 48 //2s+1 是左子节点在数组中的位置,本来s+1是父节点在二叉树中的位置,2*(s+1) 是左子节点在二叉树中的位置,那么左子节点在数组中的位置为2*(s+1)-1,简化就为2s+1了 49 //为什么需要这个for循环?很多人不理解,觉得这个方法里只需要找到父节点和两个子结点最大的一个即可,这是因为忽略了一个小问题,看下面到152行的解释应该就明白了。 50 for(child=s*2+1; child <= length-1; child=child*2+1){ //child <= length-1 说明肯定有子节点,如果child=length-1,说明只有左结点 51 52 if(child < length-1&&array[child] < array[child+1]){//child<length-1,就说明肯定右子结点,将其进行比较,找出大的一方的数组下标 53 child++; //变成右子节点所在数组中的下标,找到那个较大的子节点 54 } 55 if(array[child] > temp){ //将子节点(可能是左结点,也可能是右结点,就看上面这个判断了)与父节点进行比较,子节点大的话,将大的赋给父节点 56 array[s] = array[child]; 57 }else{ //父节点大,什么也不做,跳出这层循环。 58 break; 59 } 60 61 array[child] = temp; //父结点变为最大时,要将原先的父节点的值给现在的子节点。 62 s = child; //因为子节点的值变了,那么就不知道这个子节点在他自己的两个子节点中是否还是最大,所以需要将该子节点的数组下标给s,去重新检测一遍。只有当父节点为最大时,才会执行break退出循环。 63 64 } 65 66 67 68 }
九、总结比较各种排序算法的优缺点

1、注意,排序的稳定性的意思是:举例说明。
排序前:5,6(1),1,4,3,6(2),(第一个6在第二个6之前)
排序后:如果排序后的结果是1,2,3,4,5,6(1),6(2)那么就说此排序算 法是稳定的,反之为不稳定
2、当待排序记录个数n较大,并且是无序序列,对稳定性不作要求时,采用快速排序为宜
3、当待排序记录个数n较大,内存空间允许,要求排序稳定时,采用归并排序为宜
4、当待排序记录个数n较大,且序列中可能出现正序或逆序的情况,不要求稳定性,采用堆排序或归并排序为宜
5、等等。。。这种直接到百度上一搜,肯定会有人总结的,并且总结的肯定比我好,我就了解各种排序算法原理,如何用java进行实现,和基本的一点特性。对自己要求更高的同学则需要继续深入研究一下。。




