菜鸟记录:c语言实现PAT甲级1003--Emergency
久违的PAT,由于考研408数据结构中有一定需要,同时也是对先前所遗留的竞赛遗憾进行一定弥补 ,再次继续PAT甲级1003.。
As an emergency rescue team leader of a city, you are given a special map of your country. The map shows several scattered cities connected by some roads. Amount of rescue teams in each city and the length of each road between any pair of cities are marked on the map. When there is an emergency call to you from some other city, your job is to lead your men to the place as quickly as possible, and at the mean time, call up as many hands on the way as possible.
Input Specification:
Each input file contains one test case. For each test case, the first line contains 4 positive integers: N (≤500) - the number of cities (and the cities are numbered from 0 to N−1), M - the number of roads, C1 and C2 - the cities that you are currently in and that you must save, respectively. The next line contains N integers, where the i-th integer is the number of rescue teams in the i-th city. Then M lines follow, each describes a road with three integers c1, c2 and L, which are the pair of cities connected by a road and the length of that road, respectively. It is guaranteed that there exists at least one path from C1 to C2.
Output Specification:
For each test case, print in one line two numbers: the number of different shortest paths between C1 and C2, and the maximum amount of rescue teams you can possibly gather. All the numbers in a line must be separated by exactly one space, and there is no extra space allowed at the end of a line.
Sample Input:
5 6 0 2
1 2 1 5 3
0 1 1
0 2 2
0 3 1
1 2 1
2 4 1
3 4 1
Sample Output:
2 4就是说一个救援队,在地图所给N个的城市里进行救援,每个城市之间有M条路进行连接且有一定数量的救援人员,C1是初始地点,C2是目的地。
所需输入第一行是:城市数量、路径数量、初始地、目的地
第二行是:各城市所包含的救援人数(共N个数据)
接下来的M行:地点1、地点2、1,2间的距离L
所得输出:最短路径的数量、最多得到的救援人数
题目分析
一眼图的遍历,那么能用到的方法很多,例如广度优先、深度优先、迪杰斯特拉等等,笔者在此用深度优先,迪杰斯特拉等“高级”算法往后更新。
要清楚整体大概思路:首先对数值进行输入,对于数组,初始化应是尽可能大还是尽可能小?然后深度遍历各节点时,如何遍历下去的条件是什么?如何选择路径,到达目的地之前应该怎么进入下一个节点?达到目的地后,如何判断是最小路径?如何记录和比较最多救援人数?
个人想法
那么首先对于变量的设置
1 int N, M, C1, C2;//题目所给城市数量、路径数量、初始地、目的地 2 int c1, c2, l, dis[501][501];//二维数组dis用于记录我们所输入的M行中地点1和地点2之间的距离l3 int paths, teams;//输出的两个结果:路径数,人员数 4 int mindis[501];//计算过程中记录某条路劲上的当前最短路径 5 int* cteam;//各城市的救援人数,这里其实是个数组,写成指针是为了方便在主函数中进行内存管理malloc和初始化memset
我在此均设为全局变量,因为在后续的编写中我发现会单独写出一个dfs函数,而用全局变量可以更容易调用。要清楚设为数组的条件是记录多条数据,再次如城市是否连接,各城市间的路径长度,各城市的救援人数,遍历每条路径所需要的各路径总长度(涉及比较和有下标组成的路径标识,所以需要数组记录,单纯的变量无法做到),其次对于函数的中间变量我采取即写即设,并没有在开始就尽可能将其完全想到。
然后编写数据的输入和输出。
1 //初始化dis数组,不相连的无穷大距离,自身0距离or-1?,表示距离的同时表示有无连接 2 for (int i = 0; i < 501; i++) 3 for (int j = 0; j < 501; j++) 4 if (i == j)dis[i][j] = 0;//自身距离 5 else 6 dis[i][j] = 9999999;//设为无穷大 7 8 scanf("%d%d%d%d", &N, &M, &C1, &C2); 9 cteam = malloc(sizeof(int) * 4); 10 memset(cteam, 0, sizeof(cteam) * 4);//记录每个城市的team数,初始为0个救援人员 11 for (int i = 0; i < N; i++) { 12 scanf("%d", &cteam[i]); 13 } 14 for (int i = 0; i < M; i++) { 15 scanf("%d%d%d", &c1, &c2, &l); 16 dis[c1][c2] = l; 17 dis[c2][c1] = l; //无向图,c1->c2==c2->c1,所以两个距离相等 18 } 19 for (int i = 0; i < 501; i++)mindis[i] = 9999999; //需要注意的是这里mindis用于存放某条路径的长度,设为一个无穷大的是为了在后续比较中让我们所输入的“非无穷大”的距离记录并比较 //换句话说,如果这里初始为0,那么往后输入、记录的每条有效路径的长度都会大于0,从而导致最短路径无法更新 20 dfs(C1, 0, cteam[C1]);//深度遍历函数 21 printf("%d %d", paths, teams);
接下来就是dfs函数的编写,在次先回答分析阶段的几个问题。
深度遍历各节点时,如何遍历下去的条件是什么?
条件就是我们的答案,即最短路径(这里没加上最多人数是因为得到最多人数的前提是所得的最短路径存在),所以应该满足当前所走的路径curlen小于目前为止该地的最短路径mindis[curcity],到这其实也发现mindis数组不仅记录到该节点有无被访问,也记录历来被访问时所经历的最短路径!所以如果大于mindis,那么说明这条路径肯定不是最短,可以直接返回到上一个路径并重新选择路线;反之就继续遍历。
如何选择路径,到达目的地之前应该怎么进入下一个节点?
笔者个人对于这种所需函数相同,且需要记录的题目总是会想到迭代,大部分时候都是管用的。所以在此就是不断迭代,每次迭代下一个位置的节点、目前所走长度curlen+当前与下一个节点的距离dis、目前所有人员数+下一个节点所有人员数。
达到目的地后,如何判断是最小路径?如何记录和比较最多救援人数?
该路径目前的长度curlen是否与目标地的mindis相同,(第一次遍历的时候应是不同)不同时,将path归为1,记录当前team人数,并将此时的curlen视为最短路径对目标地的mindis赋值;相同时,path++,比较并记录最新的最多人数。这里指出 必须分为不同或相同的情况,不可以大于或小于 --> path在此时总是归为1,因为如果大于mindis只会存在第一次到达目的地时mindis初始无穷大的状态,后续在抵达,如果有比第一次到达路径长的情况会在往次迭代被终止;如果小于,那么最短路径和数量就会更新,path归为1。
1 void dfs(int curcity, int curlen, int curteam) {//每次传入节点,路径长,队伍人员 2 if (curlen > mindis[curcity])return; //如果比该节点所记录的最短路径要短,直接退出 3 if (curcity == C2) { //到达目的地,并判断是否是最短路径 4 if (curlen != mindis[curcity]) { //是最新的最短路径 5 paths = 1; 6 mindis[C2] = curlen; 7 teams = curteam; 8 } 9 else { //相同的最短路径 10 paths++; 11 if (curteam > teams)teams = curteam; 12 } 13 } 14 else 15 { 16 if (curlen < mindis[curcity])mindis[curcity] = curlen; //不大于当前最短路径时,更新最短节点 17 for (int i = 0; i < 501; i++) { 18 if (dis[curcity][i] != 9999999 && i != curcity) //遍历每个节点,同时选择有效路径进行迭代 19 dfs(i, curlen + dis[curcity][i], curteam + cteam[i]);//叠加路径长度和人员数量 20 } 21 } 22 }
<-----------------------------------完整代码----------------------------------->

#include<stdio.h> #include<stdlib.h> #include<string.h> int N, M, C1, C2; int c1, c2, dis[501][501]; int l; int paths, teams; int mindis[501]; int* cteam; void dfs(int curcity, int curlen, int curteam) { if (curlen > mindis[curcity])return; if (curcity == C2) { if (curlen != mindis[curcity]) { paths = 1; mindis[C2] = curlen; teams = curteam; } else { paths++; if (curteam > teams)teams = curteam; } } else { if (curlen < mindis[curcity])mindis[curcity] = curlen; for (int i = 0; i < 501; i++) { if (dis[curcity][i] != 9999999 && i != curcity) dfs(i, curlen + dis[curcity][i], curteam + cteam[i]); } } } int main() { //初始化dis数组,不相连的无穷大距离,自身0距离or-1? for (int i = 0; i < 501; i++) for (int j = 0; j < 501; j++) if (i == j)dis[i][j] = 0; else dis[i][j] = 9999999;//设为无穷大 scanf("%d%d%d%d", &N, &M, &C1, &C2); cteam = malloc(sizeof(int) * 4); memset(cteam, 0, sizeof(cteam) * 4);//记录每个城市的team数 for (int i = 0; i < N; i++) { scanf("%d", &cteam[i]); } for (int i = 0; i < M; i++) { scanf("%d%d%d", &c1, &c2, &l); dis[c1][c2] = l; dis[c2][c1] = l; } for (int i = 0; i < 501; i++)mindis[i] = 9999999; dfs(C1, 0, cteam[C1]); printf("%d %d", paths, teams); return 0; }
最后最后
我自己的VS2022多次实验是没有问题的,但是PAT就。。。。
多次调试甚至结果都没有,只是提醒scanf出现return问题,反复看了很多次无解,就很无奈。。。在此还是希望各位看官可以帮我找找问题并指正,不胜感激!
<-----------------------------------完整代码----------------------------------->
1 #include<stdio.h> 2 #include<string.h> 3 #define inf 1e8 4 #define max 500 5 int t = inf; 6 int den = 0, maxN = 0;//den:不同路径数, maxN:最大救援数 7 int mat[max][max];//节点之间的权值 8 int city[max];//各节点救援队数 9 int v[max];//记录节点是否已经被访问 10 int n, m, c1, c2; 11 void dfs(int c1, int c2, int dist, int num);//初始节点(中间节点),目标节点,权值,救援队数量 12 int main() { 13 scanf("%d %d %d %d", &n, &m, &c1, &c2); 14 memset(v, 0, n); 15 for (int i = 0; i < n; ++i) { 16 scanf("%d", &city[i]); 17 } 18 for (int i = 0; i < n; ++i) { 19 for (int j = 0; j < n; ++j) { 20 mat[i][j] = inf; 21 } 22 } 23 for (int i = 0; i < m; ++i) { 24 int start, end, len; 25 scanf("%d %d %d", &start, &end, &len); 26 mat[start][end] = mat[end][start] = len; 27 } 28 dfs(c1, c2, 0, city[c1]); 29 printf("%d %d", den, maxN); 30 return 0; 31 } 32 void dfs(int c1, int c2, int dist, int num) { 33 34 if (c1 == c2) { 35 if (dist < t){ 36 den = 1; 37 t = dist; 38 maxN = num; 39 } 40 else if (dist == t) { 41 den++; 42 if (maxN < num) maxN = num; 43 } 44 return ; 45 } 46 if (dist > t) return ;//剪枝 47 48 49 for(int i = 0; i < n; ++i) { 50 if (!v[i] && mat[c1][i] != inf) { 51 v[i] = 1; 52 dfs(i, c2, dist+mat[c1][i], num+city[i]); 53 v[i] = 0; 54 } 55 } 56 }
附赠大佬的满分代码,仅供参考。
<------------------------------- 更新 ------------------------------->
在上述大佬的满分代码中,我仔细观察、理解后并未发现我的错误,只是其中在迭代的部分出现了以下代码
1 if (!v[i] && mat[c1][i] != inf) { 2 v[i] = 1;//标记为经过此节点 3 dfs(i, c2, dist+mat[c1][i], num+city[i]); 4 v[i] = 0;//标记回未经过此节点 5 }
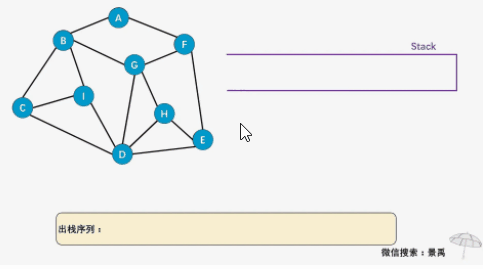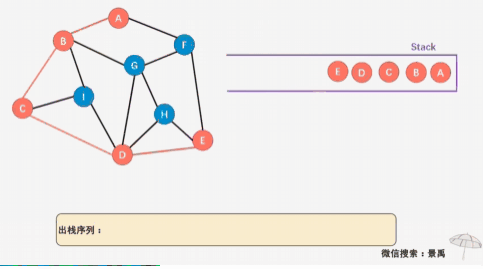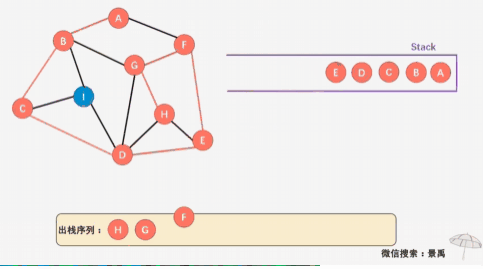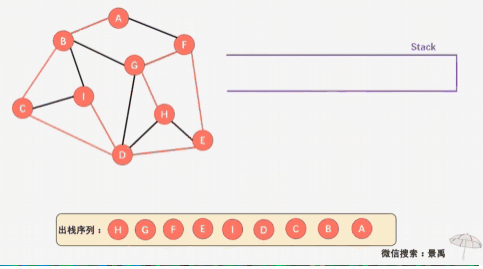
多数的参考代码中均提到了这种标记数组,但是笔者先前认为minidis数组不仅可以记录最小距离也能兼备标记的作用,于是没有改正。但在学习深度遍历和广度遍历的时候,看到了一篇文章,其中的图解让我茅塞顿开,深度遍历在无向图中的每条路径是没走完的!尤其再次提醒我经常遗忘、糊涂的一点,递归是需要返回的! 而如同图中显示的一样,在返回的过程中,先前的节点无论是采用我所写的mnidis数组还是多数写法用到的标记数组,都因为标记了经过此节点而在返回的过程中被掠过,导致更多的路线为别探寻,也就少了更多可能,这点在于广度优先遍历对比极为明显。
所以对原有的代码只需添加一个标记数组,并在循环递归前标为经过,递归后还原即可。
总结
第三题从某种意义来说是真正需要思考的题目,考的虽然是图,但还是很简单的一种,对于此题,无它,看懂图,理清每条思路即可,有必要说的是,对于竞赛也好,Leecode和洛也好,c的问题貌似总是大于c++的,也不知道现在改c++还能不能来的及。。。
感谢您能看到这,菜鸟记录,挑战每种错误的极限!