线代2

上一章矩乘里讲了基本的线代常识，这里接着讲相关的行列式

• 行列式几何意义是一个空间经过了矩阵所代表的的线性变换后，原来单位面积的经过的变换。

• 那么往特殊情况上想就是说我们只要看行列式是否为0，即可知我们是否把该空间压缩到更小的维度上对于完整概念下的行列式而言，它虽然在描述面积 但是是允许出现负值的（在这里，当二维空间发生翻转是，即可看为负值）

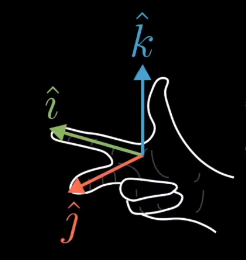
对于三维空间而言，线性变换后得到的大概率是一个平行六面体，为了像在二维下一样考虑负值，有了大概这么个右手定，则换手即为负

定义完了，接下来照例是计算方法以及为什么
对于矩阵[[a,c][b,d]] (a,c为一列，b,d为一列)，其行列式 det=ad - bc
det=(a+b)(c+d)- 1/2ac*2 - 1/2bd*2 -2bc = ad - bc;//大矩形减去两角
下面进行推广

1. 对于三维det计算，推导过程实在难以记录过程其实很大程度上可以参考混合积
   百度百科混合积传送门
   
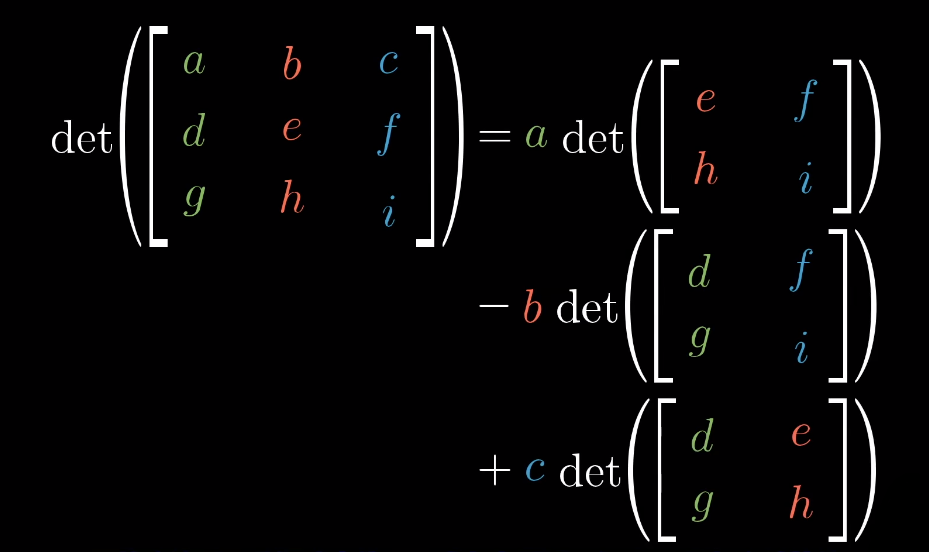
2. 对于复合线性变换而言，det(M1*M2)=det(M1)*det(M2);有了上一章复合变换左乘的底子就很好理解了

到这里就可以再插入一个内外积了。其实就是点乘和叉乘，三角函数都可以证的那种（仅仅针对二三维，点积作为投影长度是个标量，反应相似度；两个向量的叉积与这两个向量和垂直，具体见下图）