0.PTA得分截图

1.本周学习总结
1.1 总结树及串内容
思维导图

- ·串的BF\KMP算法
//BF算法(强行暴力匹配)
#include <iostream>
#include <string>
using namespace std;
int BF(string s, string p)
{
int i = 0, j = 0;
while (i < s.length() && j < p.length()) //j一旦超过模式长度,代表匹配成功,跳出循环
{
if (s[i] == p[j]) //如果当前位置匹配,则后移一位匹配下一位置
{
i++;
j++;
}
else //当前位置不匹配则回溯
{
i = i - j + 1;
j = 0;
}
}
if (j >= p.length())
{
return i - p.length(); //返回匹配成功的位置
}
else
return 0;
}
int main()
{
string s, p;
cin >> s >> p;
cout << "BF算法匹配结果为:" << BF(s, p) << endl;
return 0;
}
KMP算法
#include <iostream>
#include <string>
using namespace std;
void Getnext(int next[], string t)
{
int j = 0, k = -1;
next[0] = -1;
while (j < t.size())
{
if (k == -1 || t[j] == t[k])
{
j++;
k++;
next[j] = k;
}
else
{
k = next[k];
}
}
}
int KMP(string s, string p)
{
int next[100], i = 0, j = 0;
Getnext(next,p);
while (i <= s.size() && j <= p.size())
{
if (j == -1 || s[i] == p[j])
{
i++;
j++;
}
else
{
j = next[j];
}
}
if (j >= p.size())
{
return (i - p.size());
}
else
{
return (-1);
}
}
int main()
{
string s, p;
cin >> s >> p;
cout << "BF算法匹配结果为:" << KMP(s, p) << endl;
return 0;
}
- ·二叉树存储结构、建法、遍历及应用
//存储结构
typedef struct node
{
int data;
struct node* lchild, * rchild;
}BTnode;
typedef BTnode* BTree;
//前序创建二叉树
BTree CreateTree(string str, int &i)
{
BTree bt;
int len = str.size();
if (i > len - 1 || str[i] == '#')return NULL;
bt = new BTnode;
bt->data = str[i];
bt->lchild = CreateTree(str, ++i);
bt->rchild = CreateTree(str, ++i);
return bt;
}
//遍历输出二叉树
//前序
void PreorderPrintLeaves(BinTree BT)
{
if (BT)
{
cout<<BT->data;
PreorderPrintLeaves(BT->Left);
PreorderPrintLeaves(BT->Right);
}
}
//中序
void PreorderPrintLeaves(BinTree BT)
{
if (BT)
{
PreorderPrintLeaves(BT->Left);
cout<<BT->data;
PreorderPrintLeaves(BT->Right);
}
}
//后序
void PreorderPrintLeaves(BinTree BT)
{
if (BT)
{
PreorderPrintLeaves(BT->Left);
PreorderPrintLeaves(BT->Right);
cout<<BT->data;
}
}
应用:

代码实现
#include<iostream>
#include<string>
using namespace std;
typedef struct node
{
int data;
struct node* lchild, * rchild;
}BTnode;
typedef BTnode* BTree;
BTree CreateTree(string str, int&i);
void InorderPrintTree(BTree bt);
int main()
{
string str;
str.resize(101);
while (scanf("%s", &str[0]) != EOF)
{
BTree BT;
int i = 0;
BT = CreateTree(str, i);
InorderPrintTree(BT);
cout << endl;
}
}
BTree CreateTree(string str, int &i)
{
BTree bt;
int len = str.size();
if (i > len - 1 || str[i] == '#')return NULL;
bt = new BTnode;
bt->data = str[i];
bt->lchild = CreateTree(str, ++i);
bt->rchild = CreateTree(str, ++i);
return bt;
}
void InorderPrintTree(BTree bt)
{
if (!bt) return ;
else
{
InorderPrintTree(bt->lchild);
printf("%c ", bt->data);
InorderPrintTree(bt->rchild);
}
}
- ·树的结构、操作、遍历及应用
//存储结构
//1.双亲表示法(使用顺序存储结构)
#define MAXSIZE 100
typedef struct PTNode
{
ElemType data; //数据域
int parent; //指向双亲的游标域
}PTNode; //定义结点结构体
typedef struct
{
PTNode nodes[MAXSIZE]; //结点数组
int root; //指向根结点的游标
int count; //结点数
}PTree; //定义树结构体
//2.孩子表示法
#define MAXSIZE 100
typedef struct CTNode
{
int child; //指向长子的游标域
struct CTNode *next; //指向下一个孩子的指针域
}*ChildPtr; //定义孩子结点结构体
typedef struct
{
ElemType data; //数据域
//同双亲表示法的拓展,这里可以开个指向双亲的指针域
ChildPtr *firstchild; //指向长子的指针域
}CTBox; //定义表头结构体
typedef struct
{
PTNode nodes[MAXSIZE]; //结点数组
int root; //指向根结点的游标
int count; //结点数
}CTree; //定义树结构体
//3.孩子兄弟表示法
typedef struct Node
{
ElemType data;
int level = 0;
int contents = 0;
struct Node* bro; //指向兄弟
struct Node* child; //指向孩子
}Tnode,* Tree;
//遍历输出
void printTree(Tree root)
{
int i;
if (root == NULL)
{
return;
}
cout << root->daata << endl;
printTree(root->child);
printTree(root->bro);
}
应用:

#include<iostream>
#include<string>
using namespace std;
typedef struct Node
{
string name; //存储文件或目录名
int level = 0; //确定是几级目录或几级文件,方便输出时确定输出空格数
int contents = 0; //判断是否为目录
struct Node* bro; //指向兄弟
struct Node* child; //指向孩子
}Tnode,* Tree;
void creatTree(Tree root, string str); //建树
void printTree(Tree root); //先序遍历输出树
Tree insertNode(Tree root, string str, int flag, int lvl); //插入结点
int main()
{
int i, j, N, level, isCheck;
string str;
Tree root = new Tnode; //开辟起始节点及结点的初始化
root->contents = 1;
root->name = "root";
root->bro = root->child = NULL;
root->level = 0; //root是根目录是0级目录
root->contents = 1;
cin >> N;
for (i = 0; i <= N; i++)
{
getline(cin, str);
creatTree(root, str);
}
printTree(root); //先序遍历输出树
return 0;
}
void creatTree(Tree root, string str)
{
int lvl = 0; //记录当前目录或文件是几级目录或文件
int i, index = 0; //i用来循环遍历,index记录当前需要截取str片段的起始位置
for (i = 0; i < str.size(); i++)
{
if (str[i] == '\\') //判断是否为目录
{
lvl++;
root = insertNode(root, str.substr(index, i - index), 1, lvl);
index = i + 1;
}
}
if (index < str.size()) //如果i<str.size()则意味着读取的一行数据最后一个是文件
{
lvl++;
root = insertNode(root, str.substr(index, str.size() - index), 0, lvl);
}
}
Tree insertNode(Tree root, string str, int flag, int lvl)
{
Tree pre = root, ptr;
Tree T = new Tnode;
T->name = str; //存入文件或目录名
T->bro = T->child = NULL;
T->contents = flag; //确定是文件还是目录
T->level = lvl;
ptr = pre->child;
if (root->child == NULL)
{
root->child = T;
return root->child;
}
while (ptr != NULL && ((ptr->contents > T->contents) || (ptr->contents == T->contents && str > ptr->name)))
{
pre = ptr;
ptr = ptr->bro;
}
if (ptr == NULL)
{
T->bro = pre->bro;
pre->bro = T;
return T;
}
else if (ptr->name == T->name && ptr->contents == T->contents)
{
delete T;
return ptr;
}
else
{
if (pre->name == root->name) //插在根目录的长子位
{
T->bro = pre->child;
pre->child = T;
}
else //正常插入
{
T->bro = pre->bro;
pre->bro = T;
}
return T;
}
}
void printTree(Tree root)
{
int i;
if (root == NULL)
{
return;
}
for (i = 0; i < root->level; i++)
{
cout << " ";
}
cout << root->name << endl;
printTree(root->child);
printTree(root->bro);
}
- ·线索二叉树
//存储结构
typedef struct BiThrNode {
TElemType data; //结点数据
struct BiThrNode *lchild, *rchild; //左右孩子指针
PointerTag LTag;
PointerTag RTag; //左右标志
}BiThrNode, *BiThrTree;
//线索化的实现
oid InThreading(BiThrTree B,BiThrTree *pre) {
if(!B) return;
InThreading(B->lchild,pre);
if(!B->lchild){ //没有左孩子
B->LTag = Thread; //修改标志域为前驱线索
B->lchild = *pre; //左孩子指向前驱结点
}
if(!(*pre)->rchild){ //没有右孩子
(*pre)->RTag = Thread; //修改标志域为后继线索
(*pre)->rchild = B; //前驱右孩子指向当前结点
}
*pre = B; //保持pre指向p的前驱
InThreading(B->rchild,pre);
- ·哈夫曼树、并查集
哈夫曼树:

代码实现
#include <iostream>
using namespace std;
typedef struct
{
int weight;
int parent;
int lchild;
int rchild;
}HTNode, * HTree;
void Select(HTree HT, int k, int& idx1, int& idx2)
{
int min1 = 10000000, min2 = 10000000, i;
for (i = 1; i <= k; i++)
{
if (HT[i].parent == 0 && min1 > HT[i].weight)
{
min1 = HT[i].weight;
idx1 = i;
}
}
HT[idx1].parent = k + 1;
for (int i = 1; i <= k; i++)
{
if (HT[i].parent == 0 && min2 > HT[i].weight)
{
min2 = HT[i].weight;
idx2 = i;
}
}
HT[idx2].parent = i;
HT[k+1].lchild = idx1;
HT[k+1].rchild = idx2;
}
void CalculateWPL(HTree& HT, int n)
{
int m = 2 * n - 1, idx1, idx2, i, wpl = 0;
if (n < 0)
{
return;
}
for (i = n + 1; i <= m; i++)
{
Select(HT, i - 1, idx1, idx2);
HT[i].weight = HT[idx1].weight + HT[idx2].weight;
wpl += HT[i].weight;
}
cout << wpl;
}
int main()
{
int n, i, m;
cin >> n;
m = 2 * n - 1;
HTree HT;
HT = new HTNode[m + 1];
for (i = 1; i <= m; i++)
{
HT[i].parent = HT[i].lchild = HT[i].rchild = 0;
}
for (i = 1; i <= n; i++)
{
cin >> HT[i].weight;
}
CalculateWPL(HT, n);
return 0;
}
查并集

代码实现
#include<iostream>
using namespace std;
#define MAXSIZE 30001
typedef struct node {
int parent; //指向双亲的游标
int length; //表示朋友圈的长度
}UFSTree;
int Find(UFSTree t[], int x);
void Union(UFSTree t[], int x, int y);
int main()
{
int M, N, idx, first, count;
UFSTree t[MAXSIZE];
int i, j;
int max = 0;
cin >> M >> N;
for ( i = 1; i <= M; i++)
{
t[i].length = 0;
t[i].parent = i;
}
for ( i = 0; i < N; i++)
{
cin >> count >> first;
for ( j = 1; j < count; j++)
{
cin >> idx;
Union(t, first, idx);
}
}
for ( i = 1; i <= M; i++)
{
idx = Find(t, i);
t[idx].length++;
if (t[idx].length > max)
{
max = t[idx].length;
}
}
cout << max;
return 0;
}
int Find(UFSTree t[], int x)
{
int i;
if (t[x].parent == x)
return t[x].parent;
t[x].parent = Find(t, t[x].parent);
return t[x].parent;
}
void Union(UFSTree t[],int x, int y)
{
int idx1, idx2;
idx1 = Find(t, x);
idx2 = Find(t, y);
if (idx1 != idx2)
{
t[idx2].parent = idx1;
}
}
1.2谈谈你对树的认识及学习体会
在树这一章节,我们学习的是二叉树的算法。
树的构建:一种是直接给树的顺序存储结构的字符串,一种是通过先序遍历和中序遍历、或中序遍历和后序遍历来构造树(理解的还比较乱),还有一种哈夫曼树的构造。
在树中常常会用到递归算法,递归口的设置也是一大难点。
3.阅读代码(0--4分)
3.1

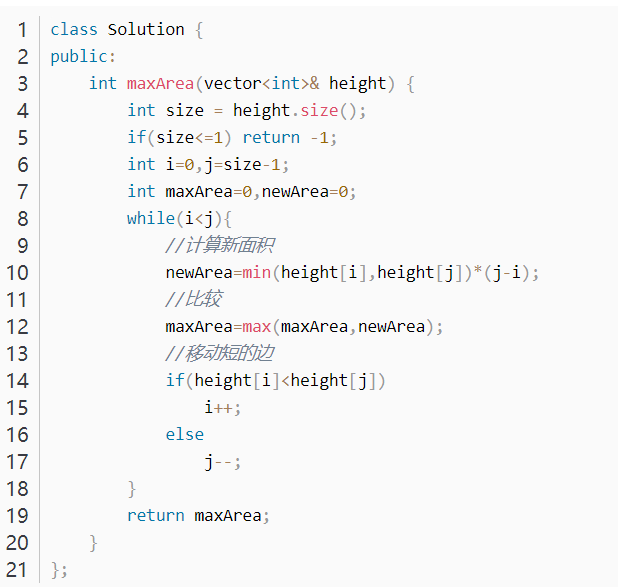
3.1.1 该题的设计思路
先在两端取两个指针,这样底边就达到了最大值,然后再考量两端的边长。然后指针再向内部移动。具体的就是让指向两边中最短边的指针向内移动,如此新的面积才可能更大。
3.1.2 伪代码
定义 int 型变量 size并赋初值 height.size()
if size<=0 //即题目中的“容器“不存在
返回 -1
end if
定义 int 型变量 i赋初值0, j赋初值size-1,maxArea,newArea均赋初值0
while i<j
计算新面积
判断新面积和之前的最大面积的大小关系,使最大面积存大的
if i对应的高度比j对应的高度小
i++
else
j++
end if
end while
返回 最大面积
3.1.3 运行结果

3.1.4分析该题目解题优势及难点。
指针的移动,小的边对应的指针移动才能求出最大容积
3.2

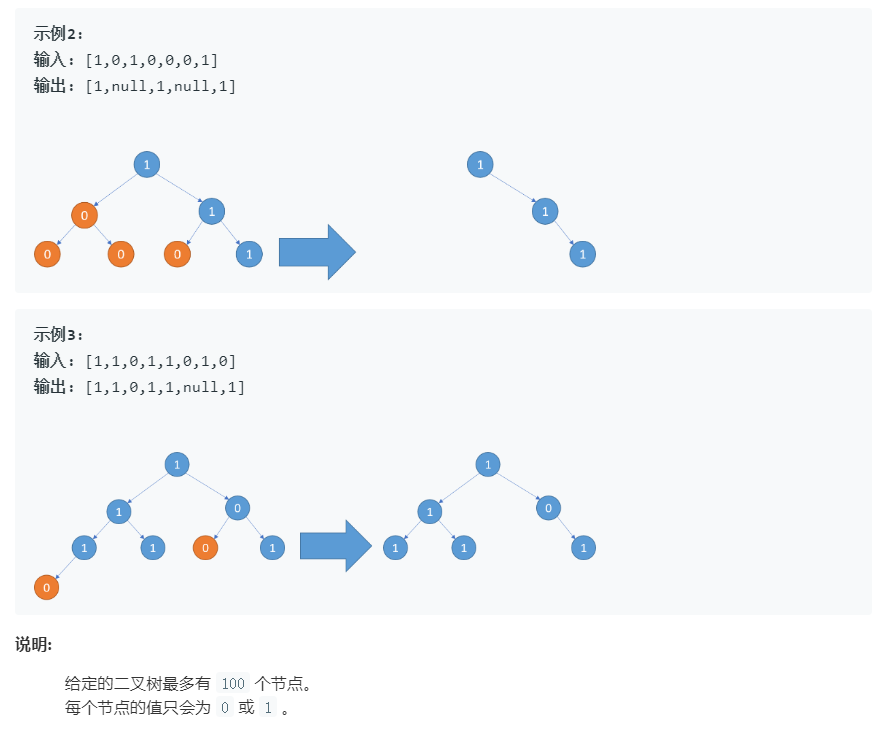
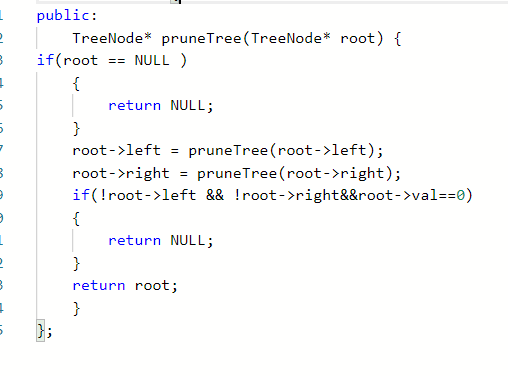
3.2.1 该题的设计思路
该题采用后序遍历的方法,若树为空,则返回NULL。接着递归左子树和右子树。若有结点左、右孩子都为空,且该结点的值为0,则返回NULL,否则返回root
3.2.2 伪代码
if root为空
返回NULL
end if
递归调用函数,判断对左右孩子进行判断
is 左右孩子均为空且结点的值为0
返回 NULL 结束循环
end if
返回 root
3.2.3 运行结果

3.2.4分析该题目解题优势及难点。
先序遍历结点并移除0结点
3.3
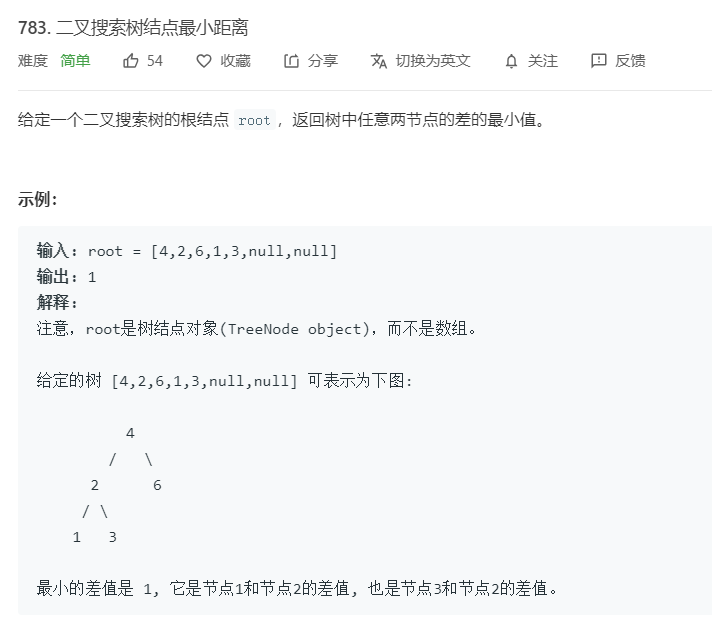
3.3.1 该题的设计思路
对最小距离的判断,要不停的递归调用自身函数
3.3.2 伪代码
void pre(vector<int>& res, TreeNode* root)
{
if root不为空
对左孩子递归调用函数
将节点的值存入res中
对右孩子递归调用函数
end if
}
int minDiffInBST(TreeNode* root)
{
定义int 型voctor容器res
以pes和root为参数调用pes函数
定义int 型voctor容器r
for i=0to res.size()-1
将res[i + 1] - res[i]存入r
end for
对r进行排序
返回 r[0]
}
3.3.3 运行结果

3.3.4分析该题目解题优势及难点。
判断两结点之间的距离,并不断比较并返回
3.4
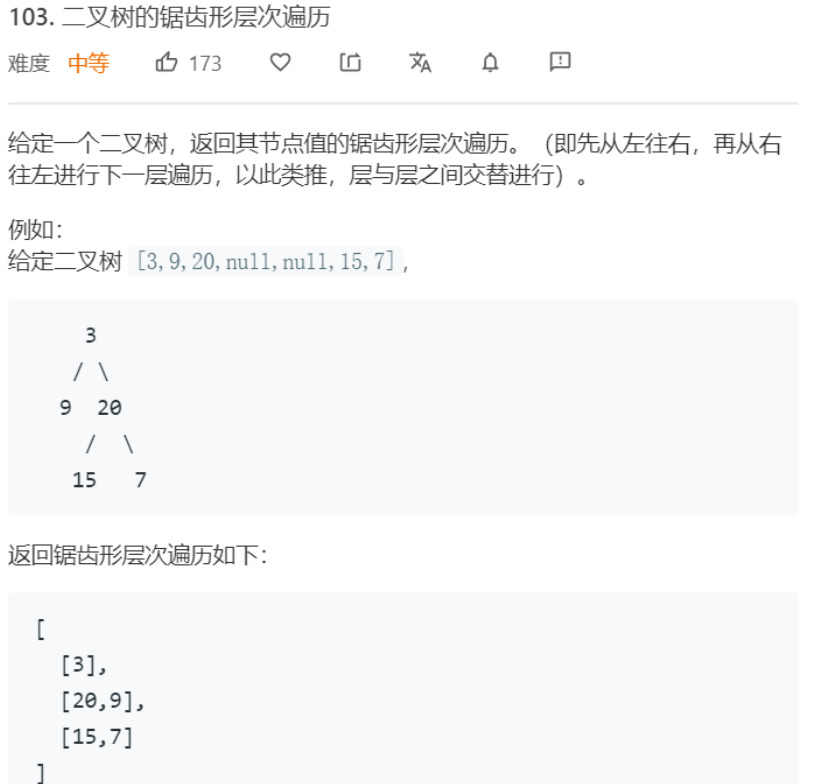

3.4.1 该题的设计思路
vector<vector<int>> zigzagLevelOrder(TreeNode* root)
{
调用递归函数
返回res
}
void addVector(TreeNode* root,int level)
{
level表示层数,也对应二维数组的第一层索引,
如果为偶数行
顺序加入
如果为奇数行
数字存到第一个位置
对左孩子和右孩子分别调用递归函数
}
3.4.3 运行结果
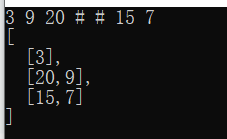
3.4.4分析该题目解题优势及难点。
通过遍历,可以将同一层级的所有节点连接起来。



