浅谈聚类算法（K-means）

   聚类算法（K-means）目的是将n个对象根据它们各自属性分成k个不同的簇，使得簇内各个对象的相似度尽可能高，而各簇之间的相似度尽量小。

   而如何评测相似度呢，采用的准则函数是误差平方和（因此也叫K-均值算法）：

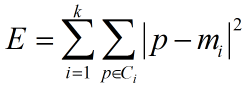其中，E是数据集中所有对象的平方误差和，P是空间中的点，表示给定对象，mi为簇Ci的均值。其实E所代表的就是所有对象到其所在聚类中心的距离之和。对于不同的聚类，E的大小肯定是不一样的，因此，使E最小的聚类是误差平方和准则下的最优结果.

选取代表点用如下几个办法：

    （1）凭经验。根据问题性质，用经验的方法确定类别个数，从数据中找出从直观上看来比较合适的代表点。

 

    （2）将全部数据随机地分成k类，计算每类的中心，将这些点作为每类的代表点。

 

    （3）“密度”选择法。这个方法思路还是比较巧妙。首先每个样本为球心，用某个正数a为半径画圈，被圈进来的样本数则成为球心样本点的“密度”。找出“密 度”最大的样本点作为第一类的代表点。然后开始选择第二类的代表点，这时不能直接选“密度”次大的代表点，因为次大的代表点很可能就在第一个代表点附近。 可以规定一个正数b，在第一个代表点范围b之外选择“密度”次大的代表点作为第二类的代表点，其余代表点按照这个原则依次进行。

 

    （4）用K个样本作为代表点。

 

    （5）采用用K-1聚类划分问题产生K聚类划分问题的代表点的方法。思路是先把所有数据看成一个聚类，其代表点为所有样本的均值，然后确定两聚类问题的代表点是一聚类问题划分的总均值和离它最远的代表点。余下的以此类推。