PCA算法和python实现
第十三章 利用PCA来简化数据
一.降维技术
当数据的特征很多的时候,我们把一个特征看做是一维的话,我们数据就有很高的维度。高维数据会带来计算困难等一系列的问题,因此我们需要进行降维。降维的好处有很多,比如:降低算法开销,让数据更加便于使用,去燥,数据更易于显示等等。
目前的降维技术主要有三种:第一种主成分分析(PCA),也就是本章介绍的内容,它只保留方差方向最大的若干个特征;第二种是因子分析,这种方法它的思想就是认为数据是由隐参数和噪声混合而成,如果我们能够找到隐参数和噪声就能够实现降维;第三种是独立成分分析(ICA),这种方法的思想是它认为数据是由若干个独立的数据源混合而成,如果我们能够找到这些数据源,就能够实现降维。
二.PCA的基本思想
PCA就是把一个高维的空间映射到一个低维的空间,这个低维的空间,让样本点的投影尽可能的分开,距离尽可能的大。要找到这样的一个低维空间,我们是通过不断的选择方差最大的方向来作为新特征维度实现的,当选择的方向的数目少于初始的特征维度,就实现了降维。
PCA算法的一般特性:
1.它的优点:降低数据的复杂度
2.它的缺点:可能用不到,会丧失一些有用的信息
3.它的使用类型:数值型数据
PCA算法实现的一般过程:
1.进行去中心化(也就是将每个数据减掉它的平均值)
2.计算XTX,也就是计算出协方差矩阵
3.计算协方差矩阵的特征向量和特征值
4.将得到的特征值进行从小到大的排列,然后选择值最大的d个特征值对应的特征向量作为新空间的方向向量
5.将数据映射到新的空间
三.PCA算法的实现
根据PC A算法的一般过程我们可以得到以下的实现方式:
首先我们需要获得数据
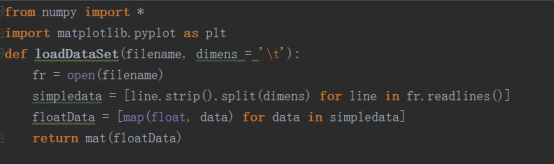
其次我们就能够定义PC A算法了
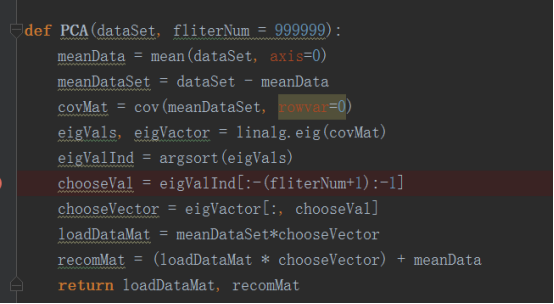
四.总结
PC A算法是一种进行降维的重要方法。我们在选择保留的特征的数目时,我们既可以实现设定,也可以根据得到特征值来进行选择。保留合适的特征数目对于数据非常的重要。
当前的降维方法主要有三种,一种是独立成分分析,一种是主成分分析,还有一种就是因子分析。主成分分析是一种应用比较广泛的方法。主成分分析他通过不断选择数据方差最大的方向来实现降维。




