寒假训练第3周(牛客冬训营)
F-Tokitsukaze and Eliminate (hard)_2024牛客寒假算法基础集训营2 (nowcoder.com)
脑袋堵住了,红温没有写出来,后面想到思路直接给否定了,可惜
题解:需要你找最右边第一个,直接先统计一下有多少个颜色的宝石,然后从左往右依次放入set到相应的颜色数就加答案,然后如果这种颜色宝石没有了就需要把一开始统计数减一下即可,后面继续放到set就好了
#include <bits/stdc++.h> //#pragma GCC optimize("Ofast") #include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> #include <cmath> //#define double long double #define int long long //#define endl '\n' using namespace std; const int N=1e6+10,M=1e1; const int INF = 0x3f3f3f3f3f3f3f3f; const int mod=998244353; typedef pair<int,int> PII; int a[N]; set<int> b; map<int,int> mp; void solve() { int n; cin>>n; for(int i=1;i<=n;i++) { cin>>a[i]; mp[a[i]]++; } int l=mp.size(); int ans=0; int c=0; for(int i=n;i>=1;i--) { b.insert(a[i]); mp[a[i]]--; if(mp[a[i]]==0) c++; if(b.size()==l) { ans++; l-=c; c=0; b.clear(); } } cout<<ans<<endl; mp.clear(); } signed main(){ std::ios::sync_with_stdio(false); std::cin.tie(nullptr); int T=1; cin>>T; while(T--){ solve(); } return 0; }
D-Tokitsukaze and Slash Draw_2024牛客寒假算法基础集训营2 (nowcoder.com)
这是一道图论题 迪杰斯特拉 想法很好,当时没有想到,一眼以为dp
题解:这道题我们可以把每一个卡牌的位置看成一个个点,然后呢,我们直接从k跑到n的一个最短路搞成一个图即可,至于怎么更新
这里就是用到dp思维了,用代价去更新,尽量寻找代价最低即可
#include <bits/stdc++.h> //#pragma GCC optimize("Ofast") #include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> #include <cmath> //#define double long double #define int long long //#define endl '\n' using namespace std; const int N=1e6+10,M=1e1; const int INF = 0x3f3f3f3f3f3f3f3f; const int mod=998244353; typedef pair<int,int> PII; void solve() { int n,m,k; cin>>n>>m>>k; priority_queue<PII,vector<PII>,greater<PII>> q; PII a[N]; for(int i=0;i<m;i++) { int x,y; cin>>x>>y; a[i]={x,y}; } vector<int> b(n+1,LLONG_MAX); b[k-1]=0; q.push({0,k-1}); while (q.size()) { auto [x,dian]=q.top(); q.pop(); if(b[dian]<x) continue; for(int i=0;i<m;i++) { auto [next,w]=a[i]; next+=dian; next%=n; if(b[next]>w+x) { b[next]=w+x; q.push({b[next],next}); } } } if(b[n-1]==LLONG_MAX) b[n-1]=-1; cout<<b[n-1]<<endl; } signed main(){ std::ios::sync_with_stdio(false); std::cin.tie(nullptr); int T=1; cin>>T; while(T--){ solve(); } return 0; }
K-Tokitsukaze and Password (easy)_2024牛客寒假算法基础集训营2 (nowcoder.com)
这是一道比较简单的题 当时没有看 一道直接暴力就行 数据范围小
题解:我们直接遍历a b c d _ 把每一个值都遍历出来,然后把他转换成一个数字 在对题目的条件判断即可,纯暴力
但是求导0的问题要注意 这里我们直接不能小于n位数的最小值即可 就是可以判掉前导0
#include <bits/stdc++.h> //#pragma GCC optimize("Ofast") #include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> #include <cmath> //#define double long double #define int long long #define endl '\n' using namespace std; const int N=1e6+10,M=1e1; const int INF = 0x3f3f3f3f3f3f3f3f; const int mod=998244353; typedef pair<int,int> PII; set<int> all; void solve() { all.clear(); int n; cin>>n; string s; cin>>s; int y; cin>>y; int minn; if(n>1) minn=pow(10,n-1); if(n==1) minn=0; for(int a=0;a<10;a++) { for(int b=0;b<10;b++) { for(int c=0;c<10;c++) { for(int d=0;d<10;d++) { if(a==b || b==c || c==d || a==c || a==d || b==d) continue; for(int k=0;k<10;k++) { int x=0; for(int i=0;i<n;i++) { if(s[i]>='0' && s[i]<='9' )x=10*x+(s[i]-'0'); if(s[i]=='a') x=x*10+a; if(s[i]=='b') x=x*10+b; if(s[i]=='c') x=x*10+c; if(s[i]=='d') x=x*10+d; if(s[i]=='_') x=10*x+k; } if(x%8==0 && x<=y && x>=minn) all.insert(x); } } } } } cout<<all.size()<<endl; } signed main(){ std::ios::sync_with_stdio(false); std::cin.tie(nullptr); int T=1; cin>>T; while(T--){ solve(); } return 0; }
M-智乃的36倍数(normal version)_2024牛客寒假算法基础集训营3 (nowcoder.com)
赛时这道题相出了一个解法,但是没有实现,就是36=4*9,然后就把两个数加起来判断是否满足模4==0模9==0
模9==0每一个数字相加等于9的倍数 模4等于0后两位可以被4整除 分别统计就可以了
接下来是另外一种思路
题解:
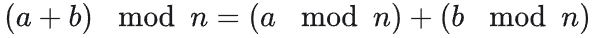
所以我们可以知道,直接分开模两个数字就可以了
然后我们先处理前面的数字,就是你要乘上多少倍放前面,我们提前把最小都模36,比如1e18模36=28然后我们就统计18位数的时候是乘28不用去乘上1e18,等于提前模36
然后我们map统计每一个数字模36的个数
枚举1到35 j
和每一个数字拼起来,然后mp[j],有就加上没有就加0就可以了,j*c[len[i]] 相当于前面的数字就是组合的第一个数
#include <bits/stdc++.h> //#pragma GCC optimize("Ofast") #include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> #include <cmath> //#define double long double #define int long long #define endl '\n' using namespace std; const int N=1e6+10,M=1e1; const int INF = 0x3f3f3f3f3f3f3f3f; const int mod=998244353; typedef pair<int,int> PII; int a[N]; void solve() { int n; cin>>n; int c[20]={0}; int t=10; map<int,int> mp; for(int i=1;i<=18;i++) { c[i]=t%36; t*=10; } int len[n+1]; for(int i=1;i<=n;i++) { cin>>a[i]; string s= to_string(a[i]); len[i]=s.size(); a[i]%=36; mp[a[i]]++; } int ans=0; for(int i=1;i<=n;i++) { for(int j=0;j<36;j++) { if((j*c[len[i]]+a[i])%36==0) { ans+=mp[j]; if(j==a[i]) ans--; } } } cout<<ans<<endl; } signed main(){ std::ios::sync_with_stdio(false); std::cin.tie(nullptr); int T=1; // cin>>T; while(T--){ solve(); } return 0; }
H-智乃的比较函数(normal version)_2024牛客寒假算法基础集训营3 (nowcoder.com)
又是一道暴力的意想不到题。。。
题解:我们直接枚举1 2 3 3 2 1 2 1 3 等这些情况,然后看看有没有一钟情况满足给出的限制条件,满足的话就说明限制条件不矛盾,枚举这些情况即可,就是直接拿来按照题目意思比大小啦 赋值比大小
#include <bits/stdc++.h> //#pragma GCC optimize("Ofast") #include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> #include <cmath> //#define double long double #define int long long #define endl '\n' using namespace std; const int N=1e6+10,M=1e1; const int INF = 0x3f3f3f3f3f3f3f3f; const int mod=998244353; typedef pair<int,int> PII; vector<array<int,3>> cmp; int a[N]; int ans; void check() { int res=0; for(auto [x,y,z]:cmp) { if(z==0){ if(a[x]<a[y]) res=1; } if(z==1) { if(a[x]>=a[y]) res=1; } } if(res==0) ans=1; } void solve() { int n; cin>>n; for(int i=1;i<=n;i++) { int x,y,z; cin>>x>>y>>z; cmp.push_back({x,y,z}); } for(int i=1;i<=3;i++) { for(int j=1;j<=3;j++) { for(int k=1;k<=3;k++) { a[1]=i,a[2]=j,a[3]=k; check(); } } } if(ans==1) cout<<"YES"<<endl; else cout<<"NO"<<endl; ans=0; cmp.clear(); } signed main(){ std::ios::sync_with_stdio(false); std::cin.tie(nullptr); int T=1; cin>>T; while(T--){ solve(); } return 0; }



