开学补题(cf版)(第四周国庆版)
题意:给你一个字符串,里面只包含A或者B两个字符
然后给你两种操作,一种是把AB变成BC,另外一种是把BA变成CB
然后问你给定的字符串最多可以变多少次
题解:我们可以发现无论你怎么搞,都要消耗一个a,所以看看B的附近有多少个A就有几次
但是假如B不够多就不可以把A全部消耗掉
比如 AAABAAAA 这里我们可以发现我们只能搞4个要去掉前面最小的那一个
因为B的区间只有1 看成一个块A块有2,B只有1,所以不行必须去掉一个最小的
如果B块大于或者等于A块那答案就是A的总和了
所以统计块数,然后要么去掉最小块数A的数量,要么就是全部
#include <bits/stdc++.h> //#pragma GCC optimize("Ofast") #include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> #include <cmath> //#define double long double #define int long long //#define endl '\n'; using namespace std; const int N=16005,M=1e1; const int INF = 0x3f3f3f3f; const int mod=100003; typedef pair<int,int> PII; void solve() { string s; cin>>s; int ans=0; int cnt=0,sum=0; int res=0; vector<int> a; for(int i=0;i<s.size();i++) { if(s[i]=='A') { cnt++; } else { if(s[i-1]=='A' || s[i+1]=='A') { res++; } if(cnt) { a.push_back(cnt); sum+=cnt; } cnt=0; } } if(cnt) sum+=cnt,a.push_back(cnt); sort(a.begin(),a.end()); if(res>=a.size()) { cout<<sum<<endl; } else { cout<<sum-a[0]<<endl; } } signed main(){ std::ios::sync_with_stdio(false); std::cin.tie(nullptr); int T=1; cin>>T; while(T--){ solve(); } return 0; }
题意:给你n张牌组里面有有负数和正数
然后给你两个操作
如果牌的位置是偶数那么你只能进行删除操作,就是删除这个位置的牌,然后全部牌向前移动一格
如果牌的位置是基数那么你可以把这张牌的值加到你自己的分数里
然后就是结束,你可以在容易位置结束
问你分数最高可以是多少
题解:首先我们从尾巴开始把全部基数的正数牌全部加起来,因为后面的数移除不会对前面的数照成影响,所以我们从尾巴开始加
然后就是剩下的正数都是偶数了,我们就要思考一下了
我们移除一张牌会影响后面数位置,也就是说,可以基数变偶数,偶数变基数,所以我们就看位置第一个数了
如果第一个数是正数,那这个数组里面的数我全部可以加上
如果不是那我们要考虑是把这个负数加上然后把后面偶数正数取出来,不然就把第二个正数去掉,让后面的数到奇数位置去
两种情况取一个就行
#include <bits/stdc++.h> //#pragma GCC optimize("Ofast") #include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> #include <cmath> //#define double long double #define int long long //#define endl '\n'; using namespace std; const int N=2e5+7,M=1e1; const int INF = 0x3f3f3f3f; const int mod=100003; typedef pair<int,int> PII; int a[N]; void solve() { int n; cin>>n; int ans=0; for(int i=1;i<=n;i++) { cin>>a[i]; if(a[i]>0)ans+=a[i]; } if(n<2) { cout<<ans<<endl; return; } else { if(a[1]<0 && a[2]>0) ans=max(ans+a[1],ans-a[2]); cout<<ans<<endl; return; } } signed main(){ std::ios::sync_with_stdio(false); std::cin.tie(nullptr); int T=1; cin>>T; while(T--){ solve(); } return 0; }
题意:给你有n个元素的数组,然后给你m个数字对
这些数字对两对立
然后让你出一个区间,在区间里不可以出现两个对立的数字对,否则就不是答案,让你统计有多少个区间可行
请举例说明:p = [1, 3, 2, 4]和敌对是 {(3, 2), (4, 2)}。区间 (1, 3) 是不正确的,因为它包含一个敌对 (3, 2)。区间 (1, 4) 也不正确,因为它包含了两个敌对 (3, 2) 和 (4, 2)。但是区间(1, 2)是正确的,因为它不包含任何敌我对。
题解:这是一个动态规划题,首先我们需要一个初始化处理
就是把每一个数字都存到对应下标里
dp数组代表 l (左区间)最远可以走多远
然后就是每一个dp[i]我们都初始化值为n,因为他们一开始都可以跑n
然后就转移

就是取最小,因为这个l中间可能还有对立数所以你要取最小
然后就从尾到头更新(因为你前一个数可以跑到哪里就决定你可以跑到哪里,就是你可以取到的最长距离)
#include <bits/stdc++.h> //#pragma GCC optimize("Ofast") #include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> #include <cmath> //#define double long double #define int long long //#define endl '\n'; using namespace std; const int N=3e5+9,M=1e1; const int INF = 0x3f3f3f3f; const int mod=1e9+7; typedef pair<int,int> PII; int dx[4]={1,-1,0,0}; int dy[4]={0,0,1,-1}; int a[N]; int biao[N]; void solve() { int n,m; cin>>n>>m; vector<int> dp(n+5,n); for(int i=1;i<=n;i++) { cin>>a[i]; biao[a[i]]=i; } for(int i=1;i<=m;i++) { int l,r; cin>>l>>r; l=biao[l]; r=biao[r]; if(l>r) swap(l,r); dp[l]=min(dp[l],r-1); } int ans=0; for(int i=n;i>=1;i--) { dp[i]=min(dp[i],dp[i+1]); } for(int i=1;i<=n;i++) { ans+=dp[i]-i+1; } cout<<ans<<endl; } signed main(){ std::ios::sync_with_stdio(false); std::cin.tie(nullptr); int T=1; // cin>>T; while(T--){ solve(); } return 0; }
题意:给你一个只包含0和1的数组,然后给你k次可以把0变成1的机会
让你变数组中的0,然后要让数组中有子串1相加出现最大数
最大化子串
题解:正常思维就是定一个左边界,然后枚举右边界,一个个字串的尝试,时间复杂度是
O(n平方)的,不太行
所以我们二分
二分1的个数即可
然后在判断函数里判断,从1开始枚举到你二分的个数,如果加上k大于等于你枚举的右长度就是可以的
记录左边界(为了改数组中的0)跳出
不断循环枚举,找到最优解即可
#include <bits/stdc++.h> //#pragma GCC optimize("Ofast") #include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> #include <cmath> //#define double long double #define int long long //#define endl '\n'; using namespace std; const int N=3e5+9,M=1e1; const int INF = 0x3f3f3f3f; const int mod=1e9+7; typedef pair<int,int> PII; int dx[4]={1,-1,0,0}; int dy[4]={0,0,1,-1}; int n,k; int a[N]; int sum[N]; int fr; bool ch(int x) { for(int i=1;i<=n-x+1;i++) { if(sum[i+x-1]-sum[i-1]+k>=x) { fr=i; return 1; } } return 0; } void solve() { cin>>n>>k; for(int i=1;i<=n;i++) { cin>>a[i]; sum[i]=sum[i-1]+a[i]; } int l=0,r=n; while (l<r) { int mid=(l+r+1)/2; if(ch(mid)) l=mid; else r=mid-1; } cout<<l<<endl; for(int i=fr;i<=fr+r-1;i++) a[i]=1; for(int i=1;i<=n;i++) cout<<a[i]<<" "; } signed main(){ std::ios::sync_with_stdio(false); std::cin.tie(nullptr); int T=1; // cin>>T; while(T--){ solve(); } return 0; }
现在插入一个我新学的算法(离散化)
引入一个例题吧802. 区间和 - AcWing题库
题意:给你一个无限长的线段,然后给你下标和一个x在这个下标上加上x就是这个下标上的值,然后询问m次,每一次给你左右边界,问你在这个范围内有值下标相加和是多少
思考:
方法1:
首先我们想到既然是下标我们中间一个数组存取,然后求一个前缀和r-(l-1)即可
但是我们发现,如果数字要是超过了1e9怎么办,数组开不了这么大呀
方法二:
我们都知道map有自动哈希的功能,它可以相当于开了一个很大的数组,所以解决了上面的麻烦
但是这个数字是一个-1e9到1e9怎么办,我们岂不是要遍历1e18次,时间复杂度直接报表,所以也不行
方法三:
现在就是离散化了,所谓离散化,就是把每一个点重新赋值
比如他要存放x的点有 1 2 3 4 122 13114 1415141
我们发现数字很大,但是个数很少,所以我们直接给每一个从1下标标到最后一个为止
也就是映射这些数1对应1 122对应5 这样,我们就好搞了
每一个数我们先二分查找他的下标。然后返回下标来搞前缀和就ok啦,
下面是一个模板代码
#include <bits/stdc++.h> //#pragma GCC optimize("Ofast") #include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> #include <cmath> //#define double long double #define int long long //#define endl '\n'; using namespace std; const int N=300010,M=1e1; const int INF = 0x3f3f3f3f; const int mod=1e9+7; typedef pair<int,int> PII; int dx[4]={1,-1,0,0}; int dy[4]={0,0,1,-1}; int n,m; vector<PII> a,b; vector<int> all; int ans[N]; int s[N]; int find(int x) { int l=0,r=all.size()-1; while (l<r) { int mid=(l+r)/2; if(all[mid]>=x) r=mid; else l=mid+1; } return r+1; } void solve() { cin>>n>>m; for(int i=0;i<n;i++) { int x,c; cin>>x>>c; a.push_back({x,c}); all.push_back(x); } for(int i=0;i<m;i++) { int l,r; cin>>l>>r; b.push_back({l,r}); all.push_back(l); all.push_back(r); } sort(all.begin(),all.end()); all.erase(unique(all.begin(),all.end()), all.end()); for(auto i: a) { int x=find(i.first); ans[x]+=i.second; } for(int i=1;i<=all.size();i++) { s[i]=s[i-1]+ans[i]; } for(auto i:b) { cout<<s[find(i.second)]-s[find(i.first)-1]<<endl; } } signed main(){ std::ios::sync_with_stdio(false); std::cin.tie(nullptr); int T=1; // cin>>T; while(T--){ solve(); } return 0; }
Problem - C - Codeforces (一道奇怪的线段树题)我感觉还是思维,不过是一道好题
题意:找出给你几条线段,这些线段可能有重合的点,现在要求你找到那些重合了k次的点
这些点可能成连续的小线段,让你输出一些连续的重复k次的线段点
题解:(这题咋一看没啥思路,我们先想暴力吧)
暴力:我们需要记录每一个点出现的次数然后用一个map进行统计
然后在遍历出满足k的点,如果线段中断我们就跳,两个点两个点的存就行
这样的时间复杂度是O(n*1e9*2)的,傻子看了都知道要爆炸,所以需要优化,而且数组还存不了负数,还得离散化,加一个log1e9*2,大爆炸
所以我们另辟蹊径
思维:
我们把全部的点都放在一个结构体数组里,然后用0和1标记他是头或者是尾巴
这里我们定头为1尾巴为0
然后一个排序结果直接出
排序以后我们就遍历
如果碰到k次1,说明他满足了k次的条件,从这开始到下一个0就是我们要的线段啦,然后遇到一个0我们就减一次,一旦满足k就把这个左断点放进数组里,到下一个0为止
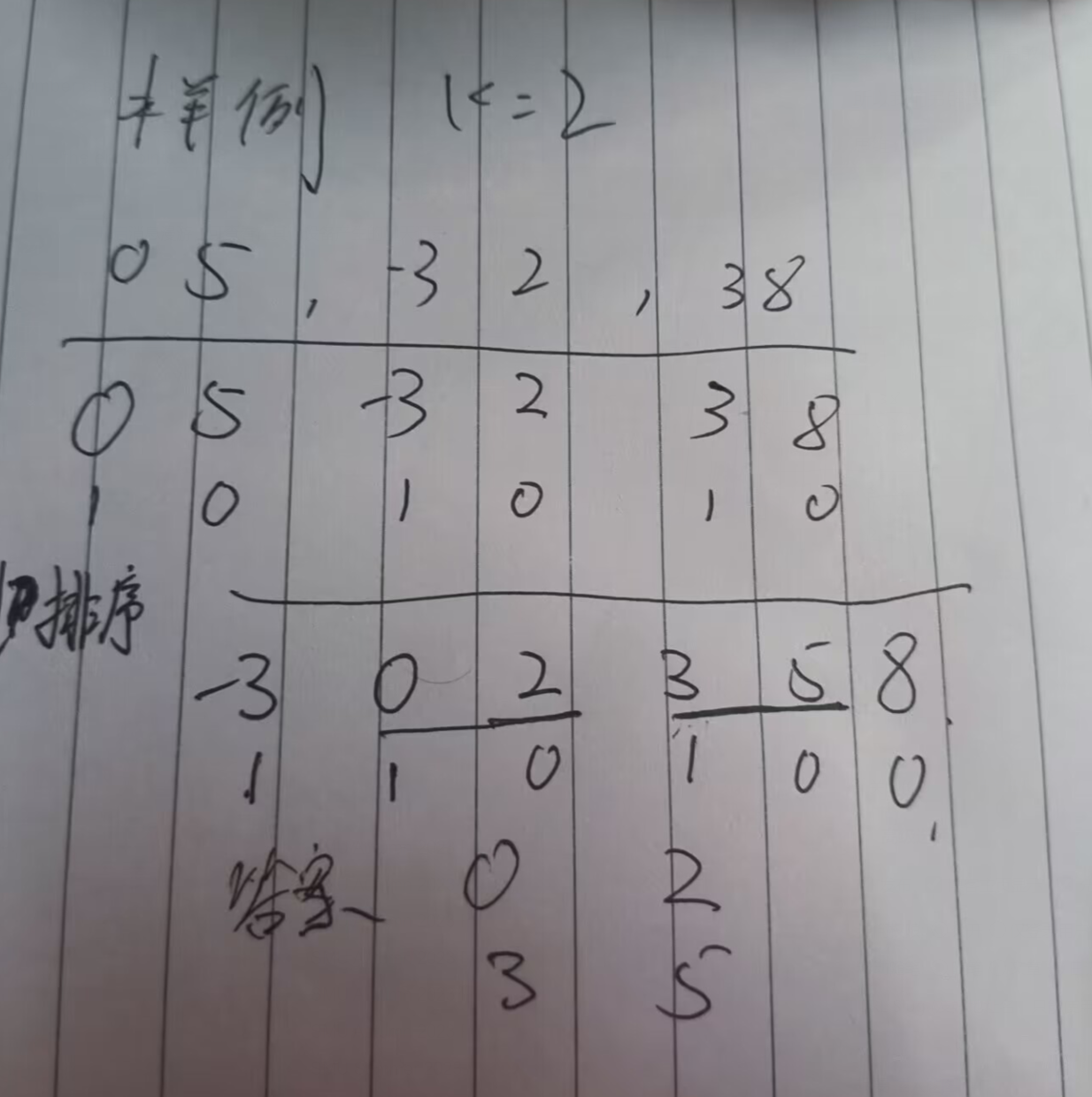
这是一个总体思维,我们去算了每一个线段对答案的贡献,而不是分开单独去看
#include <bits/stdc++.h> #pragma GCC optimize("Ofast") #include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> #include <cmath> //#define double long double #define int long long //#define endl '\n'; using namespace std; const int N=2e6+7,M=1e1; const int INF = 0x3f3f3f3f; const int mod=100003; typedef pair<int,int> PII; struct G { int l,r; }a[N]; bool cmp(G x,G y) { if(x.l==y.l) return x.r>y.r; return x.l<y.l; } void solve() { int n,k; scanf("%lld %lld",&n,&k); int op=1; for(int i=1;i<=n;i++) { scanf("%lld %lld",&a[op].l,&a[op+1].l); a[op].r=1; a[op+1].r=0; op+=2; } op-=1; sort(a+1,a+1+op,cmp); int ans=0; // for(int i=1;i<=op;i++) // { // cout<<a[i].l<<" "; // } vector<int> g; for(int i=1;i<=n*2;i++) { if(a[i].r) { ans++; if(ans==k) { g.push_back(a[i].l); } } else { if(ans==k) { g.push_back(a[i].l); } ans--; } } int x=g.size()/2; printf("%lld\n",x); int u=0; for(auto i:g) { printf("%lld ",i); u++; if(u%2==0) printf("\n"); } } signed main(){ std::ios::sync_with_stdio(false); std::cin.tie(nullptr); int T=1; // cin>>T; while(T--){ solve(); } return 0; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号