开学cf补题(第三周)(含拓扑模板)(含树上dp模板题)
首先复习一下暑假学的链表
代码都有注释,直接看即可
#include <bits/stdc++.h> //#pragma GCC optimize("Ofast") #include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> #include <cmath> //#define double long double #define int long long //#define endl '\n'; using namespace std; const int N=1e5+7,M=1e1; const int INF = 0x3f3f3f3f; const int mod=100003; typedef pair<int,int> PII; int e[N];//存储每一个需要插入的值 int en[N*2]; //存next值 就是向后的引索 int idx; //一个下标值用来开新的空间存插入的元素 int head=-1; //一开始的头时-1,这样遍历到尾巴就可以跳出 void add(int x) //在头的地方加入新的元素 { e[idx]=x; //存新加入的元素 en[idx]=head; // 把新元素的下一个next值指向原来的头 head=idx; // 更新现在的头元素 idx++; // 加加给下一个新数组开空间 } void ea(int k) //输出k后面的一个元素 { en[k]=en[en[k]]; // 把k元素的指针指向下下一个元素,直接跳过k+1元素,注意下标,因为是从0开始的 } void in(int k,int x) // 在第k个元素后面插入x { e[idx]=x; //存新的元素 en[idx]=en[k]; // 把新的元素指向k的下一个元素 en[k]=idx; // 把k元素指向刚插入的新元素 idx++; } void solve() { int m; cin>>m; while (m--) { char c; cin>>c; if(c=='H') { int x; cin>>x; add(x); } if(c=='D') { int k; cin>>k; if (k == 0) head = en[head]; else ea(k-1); //注意删除第k个输入后面的数,那函数里放的是下标,k要减去1,因为你是从0开始的 } if(c=='I') { int k,x; cin>>k>>x; in(k-1,x); } } for(int i=head;i!=-1;i=en[i]) // 遍历 { cout<<e[i]<<" "; } } signed main(){ std::ios::sync_with_stdio(false); std::cin.tie(nullptr); int T=1; // cin>>T; while(T--){ solve(); } return 0; }
然后呢就是通过链表实现的拓扑排序
这个东西可以检查是否自环
具体写法就是利用上面的链表实现
然后判断入度(一个点有几条边连向这个点那么这个点的入度就是多少),入度为0的点就是头我们就可以从头开始遍历了
然后就是判断是否自环,只要成环,那么跑完一遍拓扑,就不可能在sum数组里发现所有的点,所以我们就可以判断这里面是否有环了
(如果有环,就不可能所有的点的入队)
#include <bits/stdc++.h> //#pragma GCC optimize("Ofast") #include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> #include <cmath> //#define double long double #define int long long //#define endl '\n'; using namespace std; const int N=1e5+7,M=1e1; const int INF = 0x3f3f3f3f; const int mod=100003; typedef pair<int,int> PII; int n,m; int h[N],e[N],ne[N*2],idx; vector<int> sum; int bian[N]; void add(int x,int y) { e[idx]=y; ne[idx]=h[x]; h[x]=idx++; } void dfs() { queue<int> q; for(int i=1;i<=n;i++) { if(bian[i]==0) { q.push(i); sum.push_back(i); } } while (!q.empty()) { int t=q.front(); q.pop(); for(int i=h[t];i!=-1;i=ne[i]) { int y=e[i]; bian[y]--; if(bian[y]==0) { q.push(y); sum.push_back(y); } } } } void solve() { cin>>n>>m; ::memset(h,-1,sizeof (h)); for(int i=1;i<=m;i++) { int x,y; cin>>x>>y; add(x,y); bian[y]++; } dfs(); if(sum.size()==n) { for(int i=0;i<sum.size();i++) cout<<sum[i]<<' '; } else { cout<<-1<<" "; } } signed main(){ std::ios::sync_with_stdio(false); std::cin.tie(nullptr); int T=1; // cin>>T; while(T--){ solve(); } return 0; }
一道恶心dp,状态出就可以出,dp还是主要推关系
题意:给你一个n代表碎觉数,一个h代表一天的小时数,l和r就是如果刚好在这个时间段里睡觉那么就是好的,幸福值就++
然后给你a[i]代表在第i天时候可以在几个小时后睡觉,你可以在a[i]-1个小时睡觉,或者在a[i]个小时睡觉,主要你开始睡觉的时间在l和r之内就可以
题解:首先我们确定dp数组的含义dp[i][j]代表在第i段时间j小时的时候的满意度
然后我们就有两种选择,一个选择是a[i]小时后睡觉 ,一个是a[i]-1小时后睡觉,我们直接选最优即可
直接

这个就是如果加上a[i]后睡觉时间在l到r之间,那么就是前一个段的这个时间加1或者要原来就有的取一个max
如果加上了还是不在区间之内,那么就不能前一天的j时间段加加

就是不能+1因为在j这个时间的时候不能到l和r之间
然后就是取a[i]-1,和上面写法一样,就看能不能到目标时间段
然后就是总结
其实这两个情况写一起完全没有问题,在dp数组里肯定存的是最优的结果
因为这相当于把全部的情况都遍历了一变
全部取最优结果,好比如果你加a[i]或者a[i]-1都到区间里,所以答案更新也只是加1因为他们加的区间不同
然后只有一个能到达,那么在这dp[i][j]的时间段里只能是这个最优的答案,因为他和自己也有了max的比较
#include <bits/stdc++.h> //#pragma GCC optimize("Ofast") #include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> #include <cmath> //#define double long double #define int long long //#define endl '\n'; using namespace std; const int N=2009,M=1e1; const int INF = 0x3f3f3f3f; const int mod=100003; typedef pair<int,int> PII; int a[N]; int dp[N][N]; void solve() { int n,h,l,r; cin>>n>>h>>l>>r; memset(dp,-INF, sizeof (dp)); for(int i=1;i<=n;i++) { cin>>a[i]; } dp[0][0]=0; for(int i=1;i<=n;i++) { for(int j=0;j<h;j++) { if((j+a[i])%h>=l && (j+a[i])%h<=r) { dp[i][(j+a[i])%h]=max(dp[i][(j+a[i])%h],dp[i-1][j]+1); } else { dp[i][(j+a[i])%h]=max(dp[i][(j+a[i])%h],dp[i-1][j]); } if((j+a[i]-1)%h>=l && (j+a[i]-1)%h<=r) { dp[i][(j+a[i]-1)%h]=max(dp[i][(j+a[i]-1)%h],dp[i-1][j]+1); } else { dp[i][(j+a[i]-1)%h]=max(dp[i][(j+a[i]-1)%h],dp[i-1][j]); } } } int ans=0; for(int i=0;i<h;i++) { ans=max(ans,dp[n][i]); } cout<<ans; } signed main(){ std::ios::sync_with_stdio(false); std::cin.tie(nullptr); int T=1; // cin>>T; while(T--){ solve(); } return 0; }
一道很有趣的数学题,题目很迷惑人,像了半天,用相似三角形定理即可
题意:给你一块板子,然后让你安在格子里,问你有多少种安装方向,具体题目还是看一下里面的图
题解:首先我们先发现如果a和b相等那么就是一个正方形,无论你倒反还是正放或者斜放都一样,所以我们只需要枚举0到90°就是结果
但是如果a!=b那么就需要乘2
然后就是怎么枚举
我们可以利用矩形和x y轴围出来的三角形进行判定
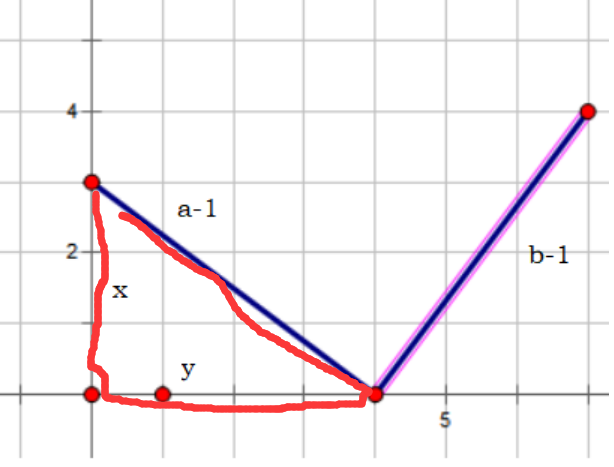
然后就是(a+x)*(a-x) || a2-x2,这个就是枚举角度了,因为一开始x==a一点点减线段就开始倾斜成三角形
然后我们在利用相似三角形求出对面的三角形的点在不在格子上即可
#include <bits/stdc++.h> //#pragma GCC optimize("Ofast") #include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> #include <cmath> //#define double long double #define int long long //#define endl '\n'; using namespace std; const int N=2009,M=1e1; const int INF = 0x3f3f3f3f; const int mod=100003; typedef pair<int,int> PII; void solve() { int a,b; cin>>a>>b; a--,b--; if(a>b) swap(a,b); int ans=1; for(int x=1;x<a;x++) { int t=(a+x)*(a-x); //相当于a^2-c^2 int y= floor(sqrt(t)); if(y*y==t || (y+1)*(y+1)==t) { if(!(x*b%a) && !(y*b%a)) //判断他的相似三角形是否在格子上 ans++; } } if(a!=b) ans*=2; cout<<ans; } signed main(){ std::ios::sync_with_stdio(false); std::cin.tie(nullptr); int T=1; // cin>>T; while(T--){ solve(); } return 0; }
P9325 [CCC 2023 S2] Symmetric Mountains - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
题意:给你n个山脉地高度,然后让你在选1到n个山脉计算两边地差值,就是头减尾巴一直往中间推,然后之和要最小就是这个个数下地最优解
然后让你输出1到n个个数地最优解,就是最小
比如
7 3 1 4 1 5 9 2
如果要5个 你可以选
[3,1,4,1,5] [1,4,1,5,9] [4,1,5,9,2] 然后计算差值选最小那个即可
这道题有两个写法
题解(双指针版)
首先我们枚举1到n就是选其中一个点当中心节点
然后我们开双指针,如果是奇数那么就会从中间开始l=r=i 然后取一个最小地差值,然后指针不断向两边扩张然后我们就不断加上
取min

这样我们可以搞出当前几个数,具体代码很容易看
#include <bits/stdc++.h> //#pragma GCC optimize("Ofast") #include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> #include <cmath> //#define double long double #define int long long //#define endl '\n'; using namespace std; const int N=5e3+7,M=1e1; const int INF = 0x3f3f3f3f; const int mod=100003; typedef pair<int,int> PII; int a[N]; int dp[N]; void solve() { int n; cin>>n; for(int i=1;i<=n;i++) { cin>>a[i]; } ::memset(dp,1e6,sizeof (dp)); for(int i=1;i<=n;i++) { int s=0; int l,r; l=r=i; while (l && r<=n) { dp[r-l+1]=min(dp[r-l+1],s); r++,l--; s+=abs(a[r]-a[l]); } s=abs(a[i+1]-a[i]); l=i,r=i+1; while (l && r<=n) { dp[r-l+1]=min(dp[r-l+1],s); r++,l--; s+=abs(a[r]-a[l]); } } for(int i=1;i<=n;i++) cout<<dp[i]<<" "; } signed main(){ std::ios::sync_with_stdio(false); std::cin.tie(nullptr); int T=1; // cin>>T; while(T--){ solve(); } return 0; }
题解2 (dp算法 区间合并)
首先枚举长度
1就等于0,所以我们从2开始
然后我们就转移
然后我们先在枚举左边界j
然后j+i-1就是i长度下的右边界然后我们就推状态转移

就是中间的数的差然后加上目前的左右边界,就是这两个数的到中间差的和了(就是从中间推两边)。
然后不断取min就行了,因为不断枚举左边界到无法枚举为止,然后这些组合里面的最小就是了
#include <bits/stdc++.h> //#pragma GCC optimize("Ofast") #include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> #include <cmath> //#define double long double #define int long long //#define endl '\n'; using namespace std; const int N=5e3+7,M=1e1; const int INF = 0x3f3f3f3f; const int mod=100003; typedef pair<int,int> PII; int a[N]; int dp[N][N]; int sum[N]; void solve() { int n; cin>>n; for(int i=1;i<=n;i++) { cin>>a[i]; } for(int i=2;i<=n;i++) { sum[i]=1e9; for(int j=1;j<=n-i+1;j++) { dp[j][i+j-1]=dp[j+1][i+j-2]+abs(a[j]-a[i+j-1]); sum[i]=min(sum[i],dp[j][i+j-1]); } } for(int i=1;i<=n;i++) cout<<sum[i]<<" "; } signed main(){ std::ios::sync_with_stdio(false); std::cin.tie(nullptr); int T=1; // cin>>T; while(T--){ solve(); } return 0; }
P1122 最大子树和 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)(树上dp模板题)
题意:就是给你一棵树,然后让你枝减去除一部分,让这个树所有节点的相加总和最大最优,就是好的
题解:一看就是树上dp模板题
用一个邻接表去存树
然后一个深度优先搜索去找到最后的点
然后从下往上去dp相加,然后发现加上来小于0那么就把那部分全部剪掉,如果大于0就dp加上,以此类推
最后去一个最大值即可
#include <bits/stdc++.h> //#pragma GCC optimize("Ofast") #include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> #include <cmath> //#define double long double #define int long long //#define endl '\n'; using namespace std; const int N=16005,M=1e1; const int INF = 0x3f3f3f3f; const int mod=100003; typedef pair<int,int> PII; int h[N]; int e[N*2],en[N*2],idx=1; int dp[N]; int a[N]; int ans=-INF; void dfs(int u,int fa) { dp[u]=a[u]; for(int i=h[u];i;i=en[i]) { int t=e[i]; if(t!=fa) { dfs(t,u); if(dp[t]>0) { dp[u]+=dp[t]; } } } ans=max(ans,dp[u]); } void add(int x,int y) { e[idx]=y; en[idx]=h[x]; h[x]=idx; idx++; } void solve() { int n; cin>>n; for(int i=1;i<=n;i++) cin>>a[i]; for(int i=1;i<n;i++) { int x,y; cin>>x>>y; add(x,y); add(y,x); } dfs(1,0); cout<<ans<<endl; } signed main(){ std::ios::sync_with_stdio(false); std::cin.tie(nullptr); int T=1; // cin>>T; while(T--){ solve(); } return 0; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号