开学大二补题(第二周)
这几天比赛发现短板很明显,写题异常慢,但是题是可以写出来的
还有就是wa的太随便动不动就是一个很简单的点给我wa了
总之,题刷少了
题意:就是给你一个棵树,这棵树分很多的叶子 一共n个点 然后让你对这个树进行层减
一共减k层 就是一层一层的去掉,然后输出还剩点的个数
题解:这道题就是一个拓扑排序的题
很好想,一层一层搞我们发现就和这些点的边数有关边数少的绝对最最低层
所以我们可以记录每一个点连起来的边数只要出度为1那么这个点就是最底层的点我们就删除即可
然后跑一个广搜 这样的首先记录现在就是1的底层点如何入队就可以了
跑队列的时候就用这些1的点因为底层的点被我们剪掉了,所以边也没了,和这些底层相连的点边数就要减减,然后减完看看这个点是不是边数只有1了
如果是那么然后减的层数不够,这点就入队,够就不入队,就行了
#include <bits/stdc++.h> #pragma GCC optimize("Ofast") #include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> #include <cmath> //#define double long double #define int long long //#define endl '\n'; using namespace std; const int N=1e6+5,M=1e1; const int INF = 0x3f3f3f3f; const int mod=998244353; typedef pair<int,int> PII; int bian[N]; int n1,k1; int dep[N]; vector<int> a[N]; int su; void bfs(int n,int k) { queue<int> q; for(int i=1;i<=n;i++) { if(bian[i]==1) { q.push(i); bian[i]=0; su++; dep[i]=1; } } while (!q.empty()) { int u=q.front(); q.pop(); for(auto x:a[u]) { bian[x]--; if(bian[x]==1 && dep[u]<k) { su++; q.push(x); dep[x]=dep[u]+1; } } } } void solve() { cin>>n1>>k1; for(int i=1;i<=n1;i++) bian[i]=0, dep[i]=1, a[i].clear(); su=0; for(int i=1;i<n1;i++) { int x,y; cin>>x>>y; a[x].push_back(y); a[y].push_back(x); bian[x]++; bian[y]++; } if(n1==1 || 2*k1>=n1) { cout<<0<<endl; return; } bfs(n1,k1); cout<<n1-su<<endl; } signed main(){ std::ios::sync_with_stdio(false); std::cin.tie(nullptr); int T=1; cin>>T; while(T--){ solve(); } return 0; }
题意:给你两种汤 第一次就是只有第一种汤,第二次是只有第二种汤,然后后面开始就把两种汤混合就行了不断混合
就是i-2次和i-1次混合出来就是第i次,不断递推下去,然后问你第n次两种汤比例是多少
题解: 其实手推的时候就会发现越是往后越是靠近1:3的比例,所以我们就知道后面大的数输出一个固定值就行了
这个点也是我卡的点(赛时卡死了)
然后前面的我们就稍微写一下模拟即可,不断相加除2不断减半即可
#include <bits/stdc++.h> #pragma GCC optimize("Ofast") #include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> #include <cmath> //#define double long double #define int long long //#define endl '\n'; using namespace std; const int N=1e6+5,M=1e1; const int INF = 0x3f3f3f3f; const int mod=998244353; typedef pair<int,int> PII; void solve() { int n; cin>>n; if(n==1) { cout<<100<<" "<<0<<endl; return; } if(n==2) { cout<<0<<" "<<100<<endl; return; } if(n==3) { cout<<50<<" "<<50<<endl; return; } if(n>=28) { cout<<"33.333333 66.666667"<<endl; return; } double a=100,b=0; for(int i=3;i<n;i++) { double t=a; a=b; b=t/2+b/2; } double ans=a*1.0/2+b*1.0/2; printf("%.6lf %.6lf",ans,100-ans); } signed main(){ std::ios::sync_with_stdio(false); std::cin.tie(nullptr); int T=1; // cin>>T; while(T--){ solve(); } return 0; }
题意:(这道题其实还算是比较简单的,思路很好想,只是赛事卡题了这道题没有去写)
给你一块l*w的地,然后给你n个种类的种子,让你用n个种子去等面积的种植,并且构造出这个矩阵。
题解:题意很简单,题的思路也是一下可以想到的,就是不太好实现,但是问题不大
l*m的矩阵我们手推一下就可以发现只要l*m%(种类数)可以除尽,那么我们就一定可以用这些种子等面积的种植在这块地里
然后我们在手推一下,如何种植呢,直接l*w/n就是一块地的面积然后对长和宽取gcd就可以知道你要的小矩形的长和宽了
然后模拟一下打出来即可
#include <bits/stdc++.h> //#pragma GCC optimize("Ofast") #include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> #include <cmath> //#define double long double #define int long long //#define endl '\n'; using namespace std; const int N=100+9,M=1e1; const int INF = 0x3f3f3f3f; const int mod=998244353; typedef pair<int,int> PII; char a[N][N]; char c[N]; void solve() { int l,w,n; cin>>l>>w>>n; if(l*w%n!=0) { cout<<"IMPOSSIBLE"<<endl; } else { int sum = l * w / n; int chang = __gcd(sum, l); sum/=chang; int kuan = __gcd(sum, w); char f = 'A'; for (int i = 1; i <= w / kuan; i++) { // cout<<f<<endl; c[i] = f; f += 1; } for (int i = 1; i <= l; i++) { int x = 1; for (int j = 1; j <= w; j++) { cout<<c[x]; if (j % kuan == 0) x++; } cout<<endl; if (i % chang == 0) { for (int k = 1; k <= w/kuan; k++) { c[k] += w/kuan; } } } } // for(int k=1;k<=l;k++) // { // for(int p=1;p<=w;p++) // { // cout<<a[k][p]; // } // cout<<endl; // } } signed main(){ std::ios::sync_with_stdio(false); std::cin.tie(nullptr); int T=1; // cin>>T; while(T--){ solve(); } return 0; }
题意:让你买东西,给你n和m,n是一共多少天,m是最多可留m天,第一个月买进然后在第i个月卖出,然后会给你第i个月卖出的价格,并且当你卖出的时候一定要买出,然后会给出当月买入的价格,必须买入,并且,你不能一直留着,连续m天后必须卖出,然后结尾要在n+1天后卖出,不需要买入了
现在问你,什么时候卖出和买入可以让总支出价格最低
题解:一看就是一个dp,只要推出状态即可
首先开一个dp[i] 代表改天的最优价格
然后我们就推状态吧
首先初始化
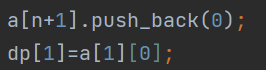
给n+1天赋一个0头,代表该天的时候不需要买入
后面的dp是直接第一天买入
开始推状态首先我们先一个for遍历n+1天
然后又一个for对前i天进行优化
首先在没有满m天的时候我们可以判断一下需不需要卖出和买进
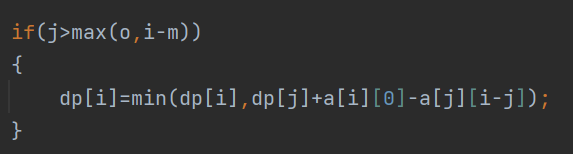
a[i][0]就是买进,然后在a[j][i-j]这是卖出的价格
然后到m天了,必须卖出
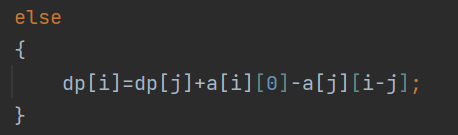
最后输出n+1即可
#include <bits/stdc++.h> //#pragma GCC optimize("Ofast") #include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> #include <cmath> //#define double long double #define int long long //#define endl '\n'; using namespace std; const int N=500010,M=1e1; const int INF = 0x3f3f3f3f; const int mod=998244353; typedef pair<int,int> PII; int dp[N]; vector<int> a[N]; void solve() { int n,m; cin>>n>>m; for(int i=1;i<=n;i++) { for(int j=0;j<=min(m,n-i+1);j++) { int x; cin>>x; a[i].push_back(x); } } a[n+1].push_back(0); dp[1]=a[1][0]; int o=1; for(int i=2;i<=n+1;i++) { for(int j=max(o,i-m);j<i;j++) { if(j>max(o,i-m)) { dp[i]=min(dp[i],dp[j]+a[i][0]-a[j][i-j]); } else { dp[i]=dp[j]+a[i][0]-a[j][i-j]; } } } cout<<dp[n+1]; } signed main(){ std::ios::sync_with_stdio(false); std::cin.tie(nullptr); int T=1; // cin>>T; while(T--){ solve(); } return 0; }
然后是我的弱项
图:
P1144 最短路计数 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
题意:给你n和m,并且给你一个图,就是点和点相连的图,然后让你找最短路,从1到每一个点的最短路,问你到每一个点最短路有多少种走法
题解:用一个邻接表来存图吧
然后我们来想一下怎么走这个最短路,我们发现一个点最短路一定经过了一个层数比它少一的结点(否则不是最短路)。
所以我们直接来广搜即可
看代码注释理解,这里就不过多赘述,模板题
#include <bits/stdc++.h> //#pragma GCC optimize("Ofast") #include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> #include <cmath> //#define double long double #define int long long //#define endl '\n'; using namespace std; const int N=100005,M=1e1; const int INF = 0x3f3f3f3f; const int mod=100003; typedef pair<int,int> PII; vector<int> a[N]; //存图 int sum[N]; //这个数组是用来计数的,就是最后输出的答案 int vis[N]; //这个是用来标记的,防止重复跑一个点 int dep[N]; //用来记步数,看看走了多少步 void bfs(int x) { queue<int> q; dep[x]=0; vis[x]=1; q.push(x); sum[x]=1; //初始化,点1 while (!q.empty()) { int op=q.front(); q.pop(); for(int i=0;i<a[op].size();i++) { int t=a[op][i]; if(!vis[t]) { vis[t]=1; //标记这个点已经走过了 dep[t]=dep[op]+1; //意思就是上一个点加1就到现在这一个点了,不断计数,看看几步到 q.push(t); //把现在这个点在放进去,再从这点开始想其他点跑 } if(dep[t]==dep[op]+1) //如果遇到了一个点加1就是当前点,那么这个点加一就是当前的最短路了 { sum[t]=(sum[t]+sum[op])%mod; //到op这个点的次数加上原来有的就是从一到t最短路的次数了 } } } } void solve() { int n,m; cin>>n>>m; for(int i=1;i<=m;i++) { int x,y; cin>>x>>y; a[x].push_back(y); a[y].push_back(x); } bfs(1); //从点1开始想其他点跑 for(int i=1;i<=n;i++) { cout<<sum[i]<<endl; } } signed main(){ std::ios::sync_with_stdio(false); std::cin.tie(nullptr); int T=1; // cin>>T; while(T--){ solve(); } return 0; }
交互题
题解:这题基本没什么思维,主打就是暴力,问题出在交互上,就是你要给出一个字符串
然后交互让他给你判断代码对错时的运行时间,你输出的字符串符合它给的时间,那就对了
思路:首先就是确定字符串的长度,大于5ms长度就对了,然后我们在一个位置一个位置去判断,一共才(字符)62*20,小于2500次所以放心暴力即可
换一个字符就问一下时间,直到时间变大,那个时候就是这个位置的字符对了,然后就可以进行下一个位置了
找位置就是(t-5)/9,就是错的位置
注意交互我们在每一个输出后面加上 fflush(stdout);进行交互
#include<iostream> #include<algorithm> #include<vector> #include<set> #include<queue> #include<math.h> #include<stack> #include<map> #include<list> #include<unordered_set> #include<unordered_map> //#define endl '\n'; //#define int long long; using namespace std; typedef long long ll; const int N = 2e5+10; int n, m, k; char ans[100] = "abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789"; string tmp; void sovle(){ int len = 1; string s = "a"; string s1,ss; int t; for (int i = 1; i <= 20; i ++){ cout << s << endl; fflush(stdout); cin>>s1>>ss; scanf(" (%d ms)",&t); if (t == 5){ s += 'a'; } else { len = i; break; } } int last=0; for (int i = 0; i < len; i ++)tmp+= 'a'; cout<<tmp<<endl; fflush(stdout); cin>>s1>>ss; scanf(" (%d ms)", &t); last = t; int pos=(t-5)/9; for (int i = pos-1; i < len; i ++){ for (int j = 0; j < 62; j ++){ tmp[i] = ans[j]; cout << tmp << endl; fflush(stdout); cin>>s1>>ss; scanf(" (%d ms)", &t); if(last<t) { last = t; int y=(t-5)/9; i=y-2; break; } } } } int main() { int t = 1; //scanf("%d", &t); while (t --){ sovle(); } return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号