暑假补题记5

题意:就是给你一个数列,让你找出可以组成等差数列的最多元素有多少个
正解:
题解:直接暴力,枚举d,然后二分查找,注意这里要枝剪,减去已经有的最大值就行了
#include <bits/stdc++.h> #include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> #include <cmath> //#define double long double #define int long long //#define endl '\n'; using namespace std; const int N=5000+7; const int INF = 0x3f3f3f3f; const int mod=998244353; int a[N]; int32_t main() { ios::sync_with_stdio(false); cin.tie(0), cout.tie(0); int n; cin>>n; for(int i=1;i<=n;i++) { cin>>a[i]; } sort(a+1,a+1+n); int ans=2; int sum=0; for(int i=1;i<n-sum;i++) { for(int j=i+1;j<=n-sum;j++) { int d=a[j]-a[i]; if(d==0) continue; int t=2; ans=2; while (binary_search(a+1,a+1+n,a[i]+t*d)) { t++; ans++; } sum=max(ans,sum); } } cout<<sum<<endl; }
题意:找山峰减两个山脚取最小的值,然后全体山峰取最大的
题解:直接On的跑,起点就是山脚单调递增跑上去,一旦开始递减那前一个地方就是山峰,然后在递减的找另外一个山脚就行了,如此循环找到最大的山峰减山脚就行了
#include <bits/stdc++.h> #include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> #include <cmath> //#define double long double #define int long long //#define endl '\n'; using namespace std; const int N=200000+5,M=1e18; const int INF = 0x3f3f3f3f; const int mod=998244353; int a[N]; int32_t main() { ios::sync_with_stdio(false); cin.tie(0), cout.tie(0); int n; cin>>n; for(int i=1;i<=n;i++) { cin>>a[i]; } int x=a[1],y=0,z=0; int ans=0,sum=0; int f=0; for(int i=2;i<=n;i++) { if(f==0) { if (a[i] >= a[i - 1]) continue; else { y = a[i - 1]; f = 1; } } if(f) { if(a[i]<=a[i-1]) { if(i!=n) continue; else { z=a[i]; ans=min((y-x),(y-z)); sum=max(ans,sum); } } else { //cout<<y<<endl; z=a[i-1]; f=0; ans=min((y-x),(y-z)); sum=max(ans,sum); x=a[i-1]; } } } cout<<sum; }
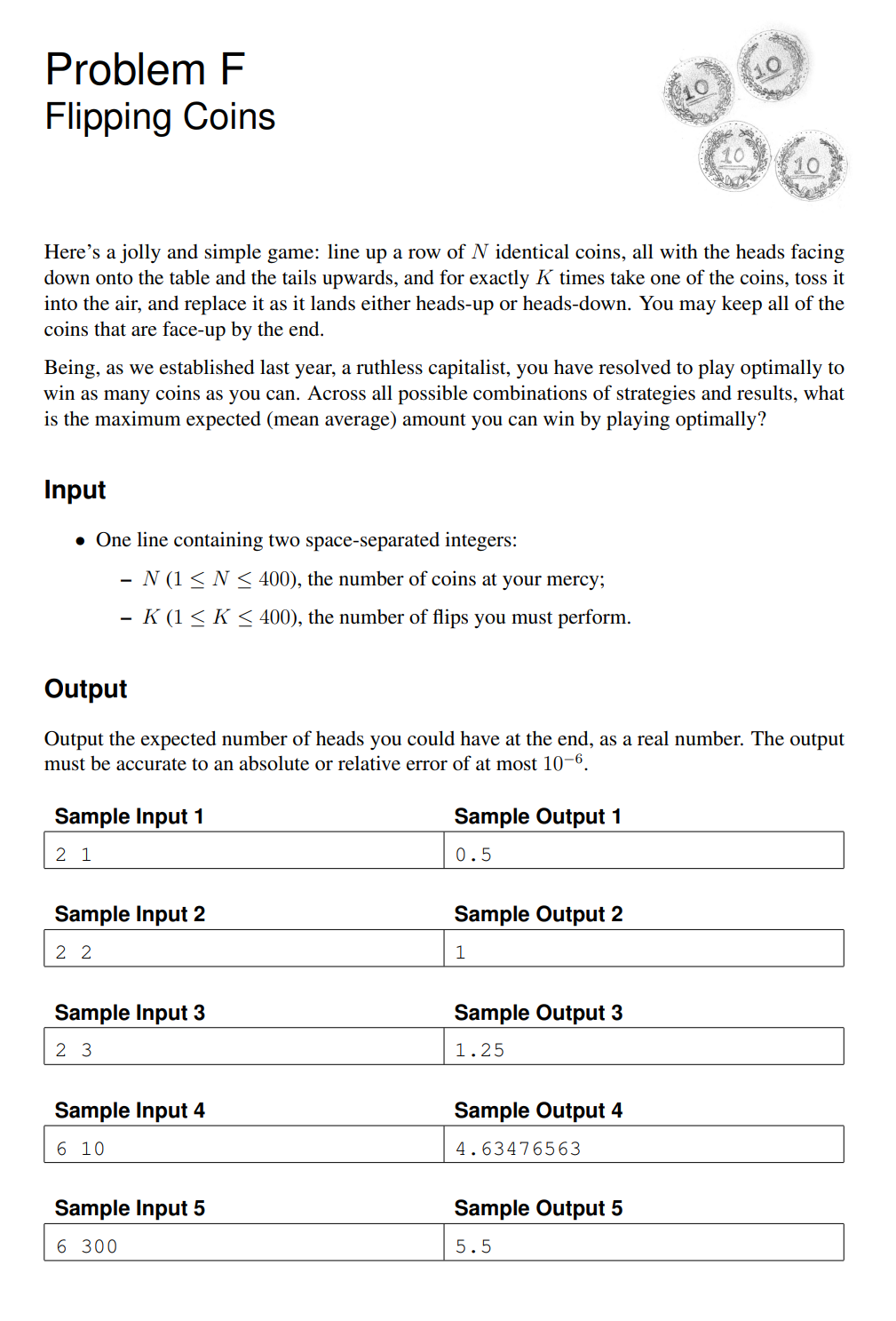
题意:起初硬币全部朝下,然后给你k次抛起来,问你有正面的最大期望
期望:=∑np,就是有n个正面的时候p概率是多少
然后就是转移方程
首先我们是正反两种情况
那么dp[i][j] i:代表抛了几次,j:代表有几次是正面
那么就开始转移
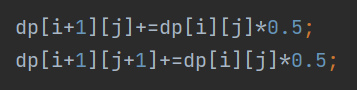
第一个是抛了个反面
第二个反之
直接累加每个硬币就是,抛了一个正加上没有抛正,但是已经到j个了两种情况相加就行了
特别的是n处
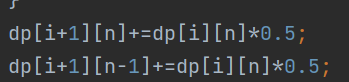
这个就是要减1,因为n个不可能再多
最后就用公式一个个×就好了
#include <bits/stdc++.h> #include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> #include <cmath> //#define double long double #define int long long //#define endl '\n'; using namespace std; const int N=450+3,M=1e18; const int INF = 0x3f3f3f3f; const int mod=998244353; double dp[N][N]; int32_t main() { ios::sync_with_stdio(false); cin.tie(0), cout.tie(0); int n,k; cin>>n>>k; dp[0][0]=1; for(int i=0;i<k;i++) { for(int j=0;j<n;j++) { dp[i+1][j]+=dp[i][j]*0.5; dp[i+1][j+1]+=dp[i][j]*0.5; } dp[i+1][n]+=dp[i][n]*0.5; dp[i+1][n-1]+=dp[i][n]*0.5; } double ans=0; for(int i=1;i<=n;i++) { ans+=dp[k][i]*i; } printf("%.8lf",ans); }
题意:自己看吧,一道期望dp加贪心
题解:排序选最大的答对概率优先,然后就是统计全不对的概率
for(int i=1;i<=n;i++) dp[i][0] = dp[i-1][0]*(1-a[i]);
然后在一个一个状态转移,很简单的方程
for(int i=1;i<=n;i++) { for(int j=1;j<=n;j++) { dp[i][j]=dp[i-1][j]*(1-a[i])+dp[i-1][j-1]*a[i]; } }
然后就是统计一下k题概率或者k+1题概率,反正不能错超过n-k道题,计算最大概率即可
i-(i-k)/2这一段意思就是k到k+1,一直k到k+2以此类堆,找最大值即可
#include <bits/stdc++.h> #include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> #include <cmath> //#define double long double #define int long long //#define endl '\n'; using namespace std; const int N=5000+5,M=1e18; const int INF = 0x3f3f3f3f; const int mod=998244353; double dp[N][N]; double a[N]; bool cmp(double x,double y) { return x>y; } int32_t main() { ios::sync_with_stdio(false); cin.tie(0), cout.tie(0); int n,k; cin>>n>>k; for(int i=1;i<=n;i++) { cin>>a[i]; } sort(a+1,a+1+n,cmp); dp[0][0]=1; for(int i=1;i<=n;i++) dp[i][0] = dp[i-1][0]*(1-a[i]); for(int i=1;i<=n;i++) { for(int j=1;j<=n;j++) { dp[i][j]=dp[i-1][j]*(1-a[i])+dp[i-1][j-1]*a[i]; } } double ans=0; for(int i=k;i<=n;i++) { double tt=0; for(int j=i-(i-k)/2;j<=i;j++) tt+=dp[i][j]; ans=max(ans,tt); } printf("%.6lf",ans); }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号