康托展开

简介：康托展开可以求解一个排列的序号，比如：12345 序号为 1  ，12354序号为2，按字典序增加编号递增，依次类推。
康托逆展开可以求解一个序号它对应的排列是什么。

 

康托展开解释：

先给出康托展开的公式：

                                                     

 

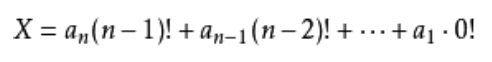
拿52413举例子：

1、首先看第一个数 5，不管第一位是什么数，后面都有四位数，那么这四位数全排列的方式有 4！种，而如果第一位是 1 或 2 或 3 或 4 都会比5开头的字典序要小，所以可以令1，2，3，4分别作为开头，这样的话就会有 4 * 4！种排法要比 52413这种排法的字典序要小。

那么第一个数是1，2，3，4时候的字典序的个数数完了是 4 * 4！ 种，且这些字典序都要比52413的字典序要小。

还有其他的排列方式比52413的字典序要小的吗？

2、那么就可以固定第一位5，找下一位2，这时5已经用过了，所以从剩下的 1，2，3，4 里挑选比2小的数，一共1个，后面还剩三位，也就是3！种排列方式，那么这时候比 52413 字典序要小的又有 1 * 3！种，也就是当5在第一位，1在第二位的时候。

3、再看第三位4，这时5，2都用了，所以从剩下的 1，3，4三个数中找比4小的数的个数，有两个比4小原理同上，所以这时候也可以有 2 * 2!种排列方式的字典序小于 52413

4、再看第四位1，这时候会有 0 * 1！种

5、再看第五位3，这时候会有0 * 0！种

 

/***** 这里以字符串进行展示  字符串可泛化性好 ******/
 
#include<iostream>
#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;
 
/*******打出1-n的阶乘表*******/
int f[20];
void jie_cheng(int n)
{
    f[0] = f[1] = 1; // 0的阶乘为1
    for(int i = 2; i <= n; i++) f[i] = f[i - 1] * i;
}
 
/**************康托展开****************/
string str;
int kangtuo()
{
    int ans = 1;  //注意，因为 12345 是算作0开始计算的，最后结果要把12345看作是第一个
    int len = str.length();
    for(int i = 0; i < len; i++){
        int tmp = 0;//用来计数的
 
        for(int j = i + 1; j < len; j++){
            if(str[i] > str[j]) tmp++;
            //计算str[i]是第几大的数，或者说计算有几个比他小的数
        }
 
        ans += tmp * f[len - i - 1];
    }
    return ans;
}
 
int main()
{
    jie_cheng(10);
    string str = "52413";
    cout<<kangtuo()<<endl;
}