寒假训练第四周

题目大意
意思就是给一个n和一个k
k是2的k次方
n是分子在2的k次方上面
从1到n
分子依次加一
然后要进行分数有理化然后把有理化的分子相加即可
思路
因为是2的k次方所以只有偶数可以有理化
那么就要找出双方的最大公约数即可
但是可能会超时
所以我们采用一层一层的除有几个k,那么偶数就要除几个2
基数无法有理化直接加即可
这里直接可以演化一个公式
n*(n+1)/2
这个是1到n相加结果
然后我们要偶数一直除k个2为止
这里可以n>>=1(意思是n除以2的1次方)(<<n)这个就是乘2的n次方
只要n=0 或者k=0就可以结束循环
#include<iostream> #include<cstring> #include <cstdio> #include<bits/stdc++.h> #include<algorithm> using namespace std; int main() { int t; cin>>t; while (t--) { long long int n,k; cin>>n>>k; long long int vis=n*(n+1)/2; while (n&&k) { n >>=1; k--; vis-=n*(n+1)/2; } cout<<vis<<endl; } }
砝码称重

这道题利用dp数组背包算法一层一层计算
首先想一下dp数组的含义
第一个dp[i]代表用上多少个砝码然后后面的 j --dp[i][j] 代表标记标记这一个结果
首先要初始化
dp[0][0]=1
然后for循环两重
第一重砝码的个数
第2重标记数组的范围
开到100000
然后循环开始
首先if(dp[i-1][j])
判断前面有没有被标记过
因为每一次加砝码都要把前面标记过的在标记在下一层数组里,最后输出只要一层的数组
so d[i][j]=1;(标记上一层已经标记过的·点)
然后一个砝码不是加就是减
所以dp[i][j+a]; dp[i][abs(j-a)];
加上绝对值不是加就是减 每一层都会有一个砝码
最后输出有几个砝码就i就等于几
在循环10000即可
#include<iostream> #include<cstring> #include <cstdio> #include<bits/stdc++.h> #include<algorithm> #include <cmath> using namespace std; int dp[105][100005]; int main() { int n,t; cin>>n; dp[0][0]=1; for(int i=1;i<=n;i++) { cin>>t; for(int j=0;j<=100000;j++) { if(dp[i-1][j]) { dp[i][j]=1; dp[i][j+t]=1; dp[i][abs(j-t)]=1; } } } int sum=0; for(int i=1;i<=100000;i++) { if(dp[n][i]) { sum++; } } cout<<sum; }

就是把字符串里的is变成was
但是难点在于
(用char 可以getline输入
但是访问很麻烦并且更改在原本char给的空间只有两个位置was放不进去
所以我用string 数组
但是输入非常麻烦
while (cin>>a[i])
{
i++;
a[i]=cin.get();
if(a[i]=="\n")
{
break;
}
}
这里面一定要加
a[i]=cin.get();
这个可以读出空格如果没有这个就无法结束循环
下面就简单了
#include <bits/stdc++.h> #include <cstdio> #include <cstring> using namespace std; string a[100000]; int main () { int i=1; while (cin>>a[i]) { i++; a[i]=cin.get(); if(a[i]=="\n") { break; } } for(int j=1;j<i;j++) { if(a[j]=="is") { if(j!=1&&j!=i-1) { a[j]="was"; } } } for(int k=1;k<i;k++) { cout<<a[k]; if(k!=i-1) { cout<<" "; } } return 0; }

这个题写出来要全部想到才可以,思路要清晰
测试用例
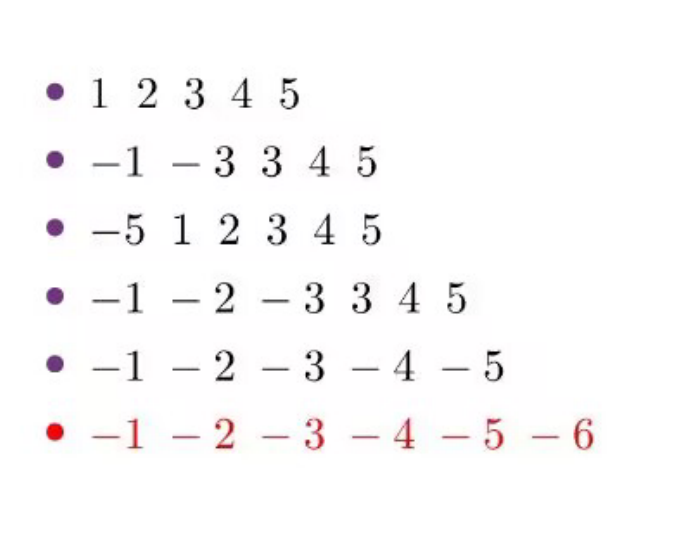
#include <bits/stdc++.h> #include <cstdio> #include <cstring> using namespace std; long long int a[300000]; int main () { int n,sum=0; cin>>n; for(int i=1;i<=n;i++) { cin>>a[i]; if(a[i]<0) { sum++; } } sort(a+1,a+n+1); if(sum!=0) { if(sum%2!=0) { cout<<a[sum]; } else { if(sum==n) { cout<<a[1]; } else { cout<<a[sum+1]; } } } if(sum==0) { cout<<a[1]; } return 0; }

这道题和中间的齿轮无关
因为线速度都相同
所以俩端比值成半径反比
换个思维就是只要数组里面有输入的比值即可
但是暴力枚举会超时
所以用离线标记法
用两个数组,一个标记半径,一个标记他们这些数的比值
#include <bits/stdc++.h> #include <cstdio> #include <cstring> using namespace std; const int N=2e5+10; int r[1000001]; int sum[N],vis[N]; int main () { int n,Q; cin>>n>>Q; for(int i=1;i<=n;i++) { int a; cin>>a; vis[a]++; } for(int i=1;i<=n;i++) { if(vis[i]==0) continue; if(vis[i]>=2) { sum[1]=1; } for(int j=2;i*j<=N;j++) { if(vis[j*i]) sum[j]=1; } } while (Q--) { int x; cin>>x; if (sum[x]) { cout << "YES" << endl; } else cout << "NO" << endl; } return 0; }

这道题动态规划
动态规划就是写出答案之前的表达式
首先要确定数组含义,然后 确定答案怎么出
初始化即可
这道题答案就是dp[n][m-1][1];
意思就是在最后一抖酒之前就必须是花
所以答案就是这个了
然后写动态方程
如果k是偶数那么之前经过的就是店
因为任何数*2都是偶数
所以只有k是偶数才有可能之前是店
也就是dp[i]-1[j][k/2]
然后还要一个是之前经过花
那样子就是dp[i][j-1][k+1]
总之就是把之前的状态写出来就可以了
#include <bits/stdc++.h> #include <cstdio> #include <cstring> using namespace std; const int N=1e9+7; int dp[105][105][105]; int main () { int n,m; cin>>n>>m; dp[0][0][2]=1; for(int i=0;i<=n;i++) { for(int j=0;j<m;j++) { for(int k=0;k<=m;k++) { if(j>0) { dp[i][j][k]=(dp[i][j][k]+dp[i][j-1][k+1])%N; } if(i>0&&k%2==0) { dp[i][j][k]=(dp[i][j][k]+dp[i-1][j][k/2])%N; } } } } cout<<dp[n][m-1][1]; return 0; }

题目意思大概就是编程一个指定条件的数组,然后输出最少改变次数
思路:
这道题没办法暴力,暴力很容易超时,思绪混乱
所以想点数学方法
题目要求a0和a1要相等
然后后面每一个数字都是前面两个数相加
所以假设a0和a1==e
那么a2==2e, a3==3e, a4==5e, a5==8e
所以我们发现都有一定倍数关系
所以我们开一个数组先求解出前面的系数也就是 1,1,2,3,5,8.·······等等就是e前面的倍数
然后再用这个除于输入的数组得出e
如果数不一样那得出的e也不一样,不一样的就要更改这样都是一个e的倍数才符合题目要求
再开一个数组
把输入的数组除e前面的倍数得出一些e然后在数组里++
得出e的次数最多那个就是可以让改变次数最少的e
输出n-e最大的次数
#include <bits/stdc++.h> #include <cstdio> #include <cstring> using namespace std; const int N=1e6+10; int a[N],f[N],vis[N]; int main () { int n,ax=-1; cin>>n; for(int i=1;i<=n;i++) { cin>>a[i]; ax=max(ax,a[i]); } f[1]=f[2]=1; int m=0; for(int i=3;i<=n;i++) { f[i]=f[i-1]+f[i-2]; if(f[i]>1e6) { m=i-1; break; } } if(m==0) { m=n; } for(int i=1;i<=m;i++) { if(a[i]%f[i]==0) { vis[a[i]/f[i]]++; } } int ans=-1; for(int i=1;i<=ax;i++) { ans=max(ans,vis[i]); } cout<<n-ans; return 0; }

这道题咋一看也就是说如果这个同一个字母是偶数就可以排成前一个后一个就可以回文
那就统计字母,因为字母有askll码值所以你也可以把字母当下标,进行遍历,记得初始化
#include <bits/stdc++.h> #include <cstdio> #include <cstring> using namespace std; const long long int N=1e5; char s[N]; int vis[N]; int main () { int t; cin>>t; while (t--) { int n; cin>>n; for(int i='a';i<='z';i++) { vis[i]=0; } for(int i='A';i<='Z';i++) { vis[i]=0; } for(int i=1;i<=n;i++) { cin>>s[i]; vis[s[i]]++; } int sum=0; for(int i='a';i<='z';i++) { if(vis[i]%2!=0) { sum=sum+vis[i]-1; } else sum=sum+vis[i]; } for(int i='A';i<='Z';i++) { if(vis[i]%2!=0) { sum=sum+vis[i]-1; } else sum=sum+vis[i]; } if(sum<n) { cout<<sum+1<<endl; } else { cout<<sum<<endl; } } return 0; }

这道题就是要排序数字的同时排序字符,然后统一输出
用struct开一个字符串和整形
然后就是cmp函数
注意看怎么写cmp函数的
#include <bits/stdc++.h> #include <cstdio> #include <cstring> using namespace std; const long long int N=100005; struct G{ int a; string s; }f[N]; bool cmp(const G &x,const G &y) { return x.a>y.a; } int main () { int n; cin>>n; for(int i=1;i<=n;i++) { cin>>f[i].a>>f[i].s; } int k; cin>>k; sort(f+1,f+n+1,cmp); cout<<f[k+1].s; return 0; }

这道题就是一个排序题,注意找规律即可
然后就是开一个string 数组 如果后面在加一个括号就是访问string[i]这个字符串中的字符
#include <bits/stdc++.h> #include <cstdio> #include <cstring> using namespace std; const long long int N=100005; string s[N]; char f; int len,k; void gg(int pi) { if(pi!=k) { cout<<s[pi]; } else for(int i=0;i<len-1;i++) { cout<<s[pi][i]; } } int main () { int t; cin>>t; while (t--) { k = 0; for (int i = 1;; i++) { cin >> s[i]; k++; len = s[i].length(); if (s[i][len - 1] == '.' || s[i][len - 1] == '!' || s[i][len - 1] == '?') { f = s[i][len - 1]; break; } } for(int i=1;i<=k/2;i++) { gg(i); cout<<" "; gg(k-i+1); if(i<k/2||k%2==1) { cout<<" "; } } if(k%2==1) { gg(k/2+1); } cout<<f<<endl; } return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号