寒假算法学习第二周
动态规划
这个东西3步走
首先给一个例子配合理解
一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
1:首先确定数组含义a[N]这个东西代表着第N级台阶的种数 也就是题目的答案
2:现在找关系假如你要跳上3级台阶那么有几种跳法
那我们可以分解一下一次可以跳1或者2
那么3级也就是当你在2时跳一步就上去了,或者当你在1时跳2就上去了
也就是说两个情况相加即可,就是你到1级台阶的跳法加上到2级台阶的跳法
有点不好讲 你就把3级分成两个情况 一个你在1级 一个你在二时 这两个情况都是即将完成的 所以你现在想知道跳3级台阶有几种情况就是你分解的这两个情况相加。
那你仔细想想 想上累加呢
3级知道了4级不就是3的情况加上2的情况吗
那么在推
n级不就是n-1的情况加上n-2的情况吗
所以表达式a[n]=a[n-1]+a[n-2];
用一个for循环一个一个依次求出来
你得到的答案将会是1--n级台阶每一级可以有多少种跳法
3:
根据上面说的回到最初我们需要两个初始数字来计算 也就是初值,跳到1级的种数和2的种数就是初值当然还有0级也是
直接赋值a[0]=0,a[1]=1,a[2]=2 3个情况的种数, 这样子2后面情况的种数我们就都可以通过公式计算出来了
现在用一题来展示
洛谷P8707
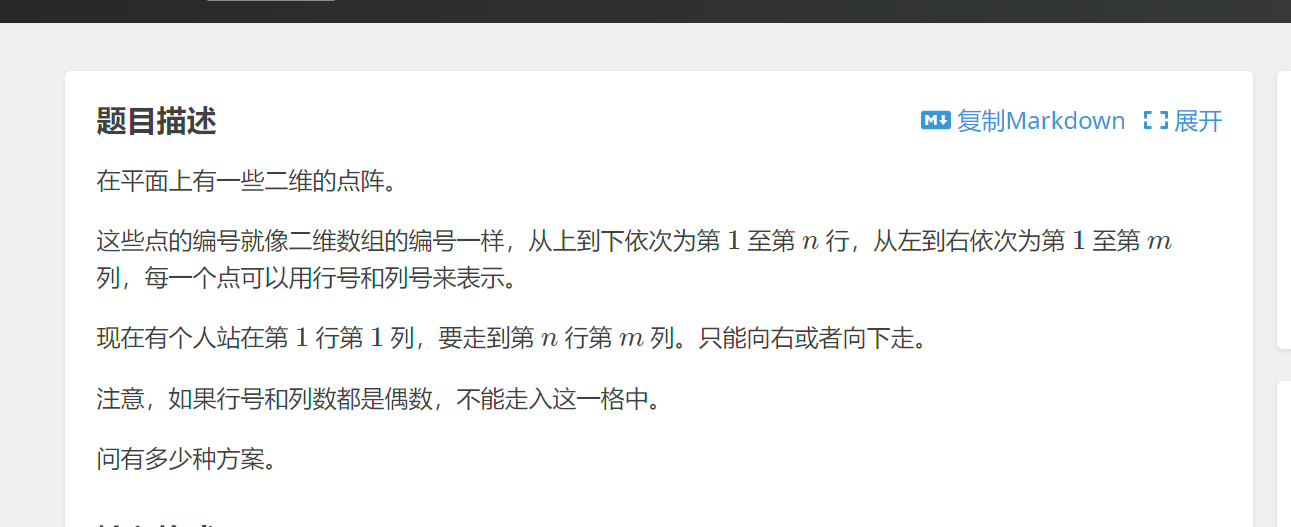
这道题是用2维数组
那就搞一个a[][]
第一步自己想好
开始第二步
这个玩意只能向下一格或者向右
那么不就是a[i][j]=a[i-1][j]+a[i][j-1]
这个就是分解两个情况
然后就是初始基层
这个的原始就是顶上一行和最左边一行
因为这两行无论怎么任意一个地方无论怎么走都只有一种方法就是一直向着那个方向走 看看规则你就明白了
给代码
#include<iostream> #include<cstdio> #include<algorithm> #include <cstring> #include<cmath> int a[40][40]; using namespace std; int main() { int n,m; cin>>n>>m; for(int i=1;i<=n;i++) { a[i][1]=1; } for(int j=1;j<=m;j++) { a[1][j]=1; } for(int i=2;i<=n;i++) { for(int j=2;j<=m;j++) { if(i%2!=0||j%2!=0) a[i][j]=a[i-1][j]+a[i][j-1]; } } cout<<a[n][m]; return 0; }
就是如此
总结
就是自己给基层数然后一步一步向上推出来,可以叫累加
前一个数由后两个数推出,注意看条件即可。
乘法表
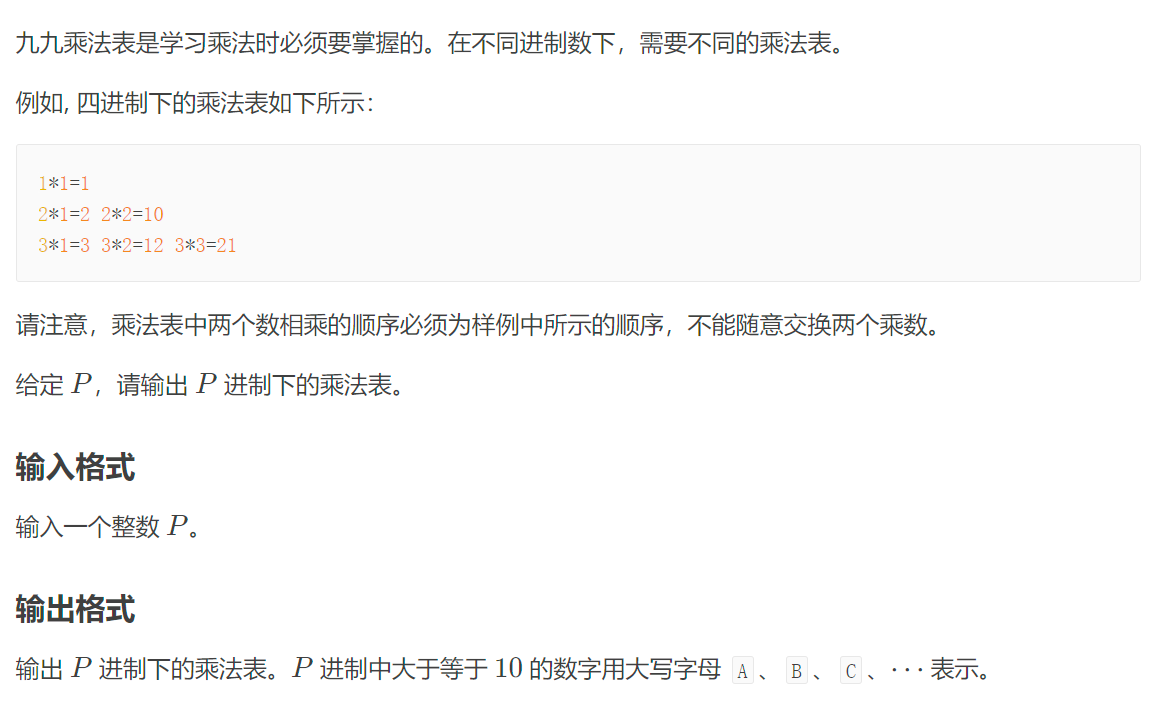
这道题其实会进制转换就ok了
对于字符转换直接用奥斯卡码值进行char(65+i-10)
首先我们来说一下通用方法
假如a=9,转换成4进制
那么应该是9/4然后取余知道a=0为止
代码实现
i=0;//就是让第一个是个位第二个是十位以此类推
while(a!=0)
{sum=a%4;
a=a/4;
sum1=sum1+a*pow(10,i)//全部相加
i++;
}
这个代码就是不断除余数就是答案,第一个余数是个位以此类推
不过在这道题里可以用一个简便方法就是
a=9 4进制
sum=a/4;//这个就是十位
sum1=a%4;//这个就是个位
两个拼接就是答案
不过这个方法仅限这个乘法表,大家还是以通用放法为准
#include<iostream> #include<cstdio> #include<algorithm> #include <cstring> #include<cmath> using namespace std; int main() { int P,sum; char ch='*'; cin>>P; for(int i=1;i<P;i++) { for(int j=1;j<=i;j++) { sum=i*j; int sum1=sum/P; int sum2=sum%P; if(i>=10) { cout<<char(65+i-10); } else { cout<<i; } cout<<ch; if(j>=10) { cout<<char(65+j-10); } else { cout<<j; } cout<<"="; if(sum1!=0) { if(sum1>=10) { cout<<char(65+sum1-10); } else { cout<<sum1; } } if(sum2>=10) { cout<<char(65+sum2-10)<<" "; } else { cout<<sum2<<" "; } } cout<<endl; } return 0; }
01背包+动态规划

那我先定义数组
v[i]是价值
w[i]是需要的空间
dp[i][j]里 i代表物品的数量,j就代表背包可以承受的空间
如果i=1,那么j<5时dp[i][j]就等于0,因为放第一个根本放不进去
j>5时那么dp[i][j]=20这个就是最优的选择
当i=2时要放钱两个外聘 如果j>6
那么你觉得会放哪一个第一个肯定是最优的怎么写因为前面i=1的dp数组我们已经给垫好初始值了
所以利用动态规划的思路一层一层递推
假设j=10;
dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i])
选最优的那个去赋值
dp[i-1][j]=就是dp[1][10]=20(前面已经给过值了)
dp[i-1][j-w[i]]=就是dp[1][4]=0所以max当然会选20以此类推
这样子要i个物品容量是j时就可以得出最优结果
注意写j的循环时最好用倒序写就是j--,从最大开始
虽然二维数组不怕这个影响,但是用简便的一维数组就会影响
具体的https://www.luogu.com.cn/problem/solution/P1048看这个博主
分享代码
#include "iostream" #include "stdio.h" using namespace std; int w[105],val[105]; int dp[105][1005]; int main() { int t,m,res=-1; scanf("%d%d",&t,&m); for(int i=1;i<=m;i++) { scanf("%d%d",&w[i],&val[i]); } for(int i=1;i<=m;i++) for(int j=t;j>=0;j--) { if(j>=w[i]) { dp[i][j]=max(dp[i-1][j-w[i]]+val[i],dp[i-1][j]); } else { dp[i][j]=dp[i-1][j]; } } printf("%d",dp[m][t]); return 0; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号