【题解】P5344 XR-1逛森林 / 【笔记】倍增优化建图
题解真**难写,*!
但是暑假要结束了,得冲点业绩,我博客写的忒少了,于是这篇题解诞生了,个人认为质量不戳,还有图呢,图画了巨**久,能当两篇的业绩了。
那我为什么不拿这个时间写两篇,是不是**
以上为我在写完后发的牢骚
本题解主要面向倍增优化建图的初学者,类似于我个人倍增优化建图的学习笔记。
前置知识:Dijkstra ,树上倍增。
思路
明显先离线把第二个操作的树建好以后再把符合条件的第一类操作加上会更方便。
具体就是先把读入操作,然后用并查集维护一下连通性判断这个操作是否合法,把合法的 2 操作直接加边,合法的 1 操作存起来。
然后处理倍增数组,将合法的 1 操作用倍增优化建图加边。
所以这题大概可以当个倍增优化建图板子(为什么这东西会有板子啊)。
倍增优化建图板子
考虑对于一条链的两个端点求 LCA 的过程,如果可以把跳一次倍增数组所越过的节点当做单独一个点的话,就可以用这个点连边而不需要每个点都走一次了。
基于这个思路,可以对于倍增所使用的 \(f\) 数组开两个虚节点,称作 \(in\) 和 \(out\) ,\(in\) 来存入边,\(out\) 来存出边,然后将倍增中下一级的 \(out\) 向本级的 \(out\) 连边,本级的 \(in\) 向下级的 \(in\) 连边。
此处建议看图理解,\(x0\) 至 \(x4\) 为树上的某条链,黑边为树边,红边为倍增的数组,附加了 \(in\)、\(out\) 结点及下标,绿边为倍增时的新加边。
(全画会很挤,图中省略了部分内容,我尽力画了,图丑勿喷)
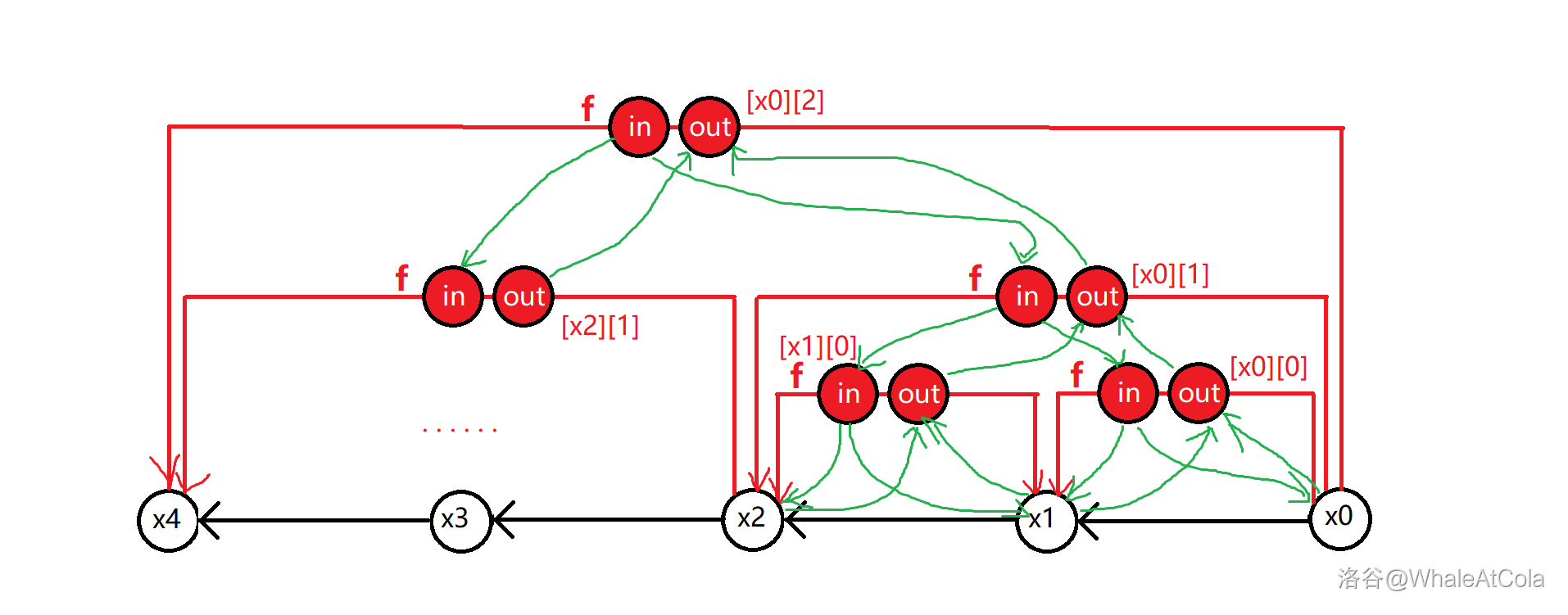
显然,这样的结点数和边数都是 \(O(n \log n)\) 的。
那么如何加边呢?1 操作中,对于边的出点,即 \(u1\) 至 \(v1\) 这条链上的点,可以在求他们的 LCA 时,每跳一次倍增数组将其 \(out\) 这个虚节点向新建的虚节点连一条权为 \(0\) 的边,同样的,对于边的入点,即 \(u2\) 至 \(v2\) 这条链上的点,可以在求他们的 LCA 时,每跳一次倍增数组将新建的虚节点向其 \(in\) 这个虚节点连一条权为 \(0\) 的边。最后把这两个新建的虚节点连一条带权边就好了。
注意如果倍增 LCA 的后半部分(即两个端点 \(x\) 和 \(y\) 深度相同后的部分)一次也没跳时,\(y\) 会没有向外连边,需要特判这种情况将 \(y\) 向外的连边补上,但是因为本题是求最短路的,直接不特判把 \(y\) 的边连上也行。
搞完建图后直接跑一遍 Dijkstra 就行了。
因 \(m \approx n \log n\),时间复杂度大致是 \(O(n \log^2 n)\) 的。
code
#include<cstdio>
#include<cstring>
#include<queue>
#include<vector>
using std::priority_queue;
using std::vector;
using std::greater;
using std::pair;
#define re register
#define pr pair<int,int>
#define fi first
#define se second
inline void swp(int &x,int &y){x^=y^=x^=y;}
inline int win(){
int x=0;char c=getchar();
while(c>'9'||c<'0') c=getchar();
while(c>='0'&&c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar();
return x;
}
const int inf=0x3f3f3f3f;
const int N=50050,M=1000050,NE=4000050,ME=16000050;
int l,tot,fa[N],v[N<<1],ne[N<<1],h[N],dep[N],f[N][16],in[N][16],ou[N][16];
int ted;
struct oprs{int x1,y1,x2,y2,w;}op[M];
int cnt,hd[NE],t;
struct edge{int v,d,n;}e[ME];
int dis[NE];
inline bool cmp(int x,int y){return dis[x]<dis[y];}
int get(int x){return fa[x]==x?x:(fa[x]=get(fa[x]));}
inline void addtree(int x,int y){
// printf("addtree:%d %d\n",x,y);
v[++tot]=y,ne[tot]=h[x],h[x]=tot;
v[++tot]=x,ne[tot]=h[y],h[y]=tot;
}
inline void addedge(int x,int y,int w){e[++t]={y,w,hd[x]},hd[x]=t;}
void dfs(int x,int fr){
dep[x]=dep[f[x][0]=fr]+1;
in[x][0]=++cnt,addedge(cnt,x,0),addedge(cnt,fr,0);
ou[x][0]=++cnt,addedge(x,cnt,0),addedge(fr,cnt,0);
for(re int j=0;j<l;j++){
f[x][j+1]=f[f[x][j]][j];
in[x][j+1]=++cnt,addedge(cnt,in[x][j],0),addedge(cnt,in[f[x][j]][j],0);
ou[x][j+1]=++cnt,addedge(ou[x][j],cnt,0),addedge(ou[f[x][j]][j],cnt,0);
}
for(re int i=h[x];i;i=ne[i]) if(v[i]!=fr) dfs(v[i],x);
}
inline void lca1(int x,int y,int k){
if(dep[x]<dep[y]) swp(x,y);
addedge(y,k,0);
for(re int i=l;i>=0;i--) if(dep[f[x][i]]>=dep[y]) addedge(ou[x][i],k,0),x=f[x][i];
if(x==y) return ;
for(re int i=l;i>=0;i--) if(f[x][i]!=f[y][i])
addedge(ou[x][i],k,0),x=f[x][i],addedge(ou[y][i],k,0),y=f[y][i];
addedge(ou[x][0],k,0);
}
inline void lca2(int x,int y,int k){
if(dep[x]<dep[y]) swp(x,y);
addedge(k,y,0);
for(re int i=l;i>=0;i--) if(dep[f[x][i]]>=dep[y]) addedge(k,in[x][i],0),x=f[x][i];
if(x==y) return ;
for(re int i=l;i>=0;i--) if(f[x][i]!=f[y][i])
addedge(k,in[x][i],0),x=f[x][i],addedge(k,in[y][i],0),y=f[y][i];
addedge(k,in[x][0],0);
}
inline void dijkstra(int s){
memset(dis,0x3f,sizeof dis);
priority_queue<pr,vector<pr>,greater<pr> > q;
dis[s]=0,q.push((pr){0,s});
pr x;
while(!q.empty()){
x=q.top(),q.pop();
if(x.fi>dis[x.se]) continue;
for(re int i=hd[x.se],y;i;i=e[i].n)
if(dis[y=e[i].v]>x.fi+e[i].d)
q.push((pr){dis[y]=x.fi+e[i].d,y});
}
}
signed main(){
int n=win(),m=win(),s=win(),kd,x1,y1,x2,y2,w;cnt=n;
while((1<<l)<=n) ++l;
l--;
// printf("%d\n",l);
for(re int i=1;i<=n;i++) fa[i]=i;
while(m--){
kd=win();
if(kd==1){
x1=win(),y1=win(),x2=win(),y2=win(),w=win();
if(get(x1)!=get(y1)||get(x2)!=get(y2)) continue;
op[++ted]={x1,y1,x2,y2,w};
}
else{
x1=win(),y1=win(),x2=get(x1),y2=get(y1),w=win();
if(x2==y2) continue;
addtree(x1,y1),addedge(x1,y1,w),addedge(y1,x1,w),fa[x2]=y2;
}
}
for(re int i=1;i<=n;i++) if(!dep[i]) dfs(i,0);
for(re int i=1;i<=ted;i++)
lca1(op[i].x1,op[i].y1,++cnt),lca2(op[i].x2,op[i].y2,++cnt),addedge(cnt-1,cnt,op[i].w);
dijkstra(s);
for(re int i=1;i<=n;i++) printf("%d ",dis[i]==inf?-1:dis[i]);
puts("");
return 0;
}
球点个赞吧,蟹蟹。

