从Leetcode的回文子串中学习动态规划和中心扩散法
动态规划和中心扩散法的学习
题目：给你一个字符串s，找到s中最长的回文子串。
示例：
输入：s="babad"
输出："bab" or "aba"
输入：s="cbbd"
输出："bb"
常规解题
我之前的思路就是遍历字符串，然后反转字符串看看是否是回文子串。
class Solution { public String longestPalindrome(String s) { char[] arr = s.toCharArray(); List<String> list = new ArrayList<>(); for(int i=0;i<arr.length;i++) { for(int j=i;j<arr.length;j++) { String str = s.substring(i,j+1); if(str.equals(reverse(str))) { list.add(str); } } } return MaxinArrySize(list); } public String reverse(String str) { String reverse = ""; int length = str.length(); for (int i = 0; i < length; i++) { reverse = str.charAt(i) + reverse; } return reverse; } public String MaxinArrySize(List<String> arrList) { int max = 0; int index = 0; for (int i = 0;i<arrList.size();i++) { String s = arrList.get(i); if (s.length() > max) { index = i; max = s.length(); } } return arrList.get(index); } }
但是提交后发现
"civilwartestingwhetherthatnaptionoranynartionsoconceivedandsodedicatedcanlongendureWeareqmetonagreatbattlefiemldoftzhatwarWehavecometodedicpateaportionofthatfieldasafinalrestingplaceforthosewhoheregavetheirlivesthatthatnationmightliveItisaltogetherfangandproperthatweshoulddothisButinalargersensewecannotdedicatewecannotconsecratewecannothallowthisgroundThebravelmenlivinganddeadwhostruggledherehaveconsecrateditfaraboveourpoorponwertoaddordetractTgheworldadswfilllittlenotlenorlongrememberwhatwesayherebutitcanneverforgetwhattheydidhereItisforusthelivingrathertobededicatedheretotheulnfinishedworkwhichtheywhofoughtherehavethusfarsonoblyadvancedItisratherforustobeherededicatedtothegreattdafskremainingbeforeusthatfromthesehonoreddeadwetakeincreaseddevotiontothatcauseforwhichtheygavethelastpfullmeasureofdevotionthatweherehighlyresolvethatthesedeadshallnothavediedinvainthatthisnationunsderGodshallhaveanewbirthoffreedomandthatgovernmentofthepeoplebythepeopleforthepeopleshallnotperishfromtheearth"
卡在这个测试用例上了，显示时间超时。
很明显，只要字符串长了，遍历所耗费的时间就呈指数增长。
动态规划法
创建一个二维数组 dp[i][j]用来存放字符S[i]和S[j]的字符是否相等，如果是，则状态为1，否则为0。其中S是字符串数组。
这样就引申出：
-
当S[i] == S[j]时，如果S[i+1] == S[j-1]，那么这个字符串就是回文子串，反之则不是回文子串。
-
当S[i] != S[j]时，则一定不是回文子串。
-
当i == j时，则是单个字符，一定为回文子串。
则可以推导出动态转移方程：
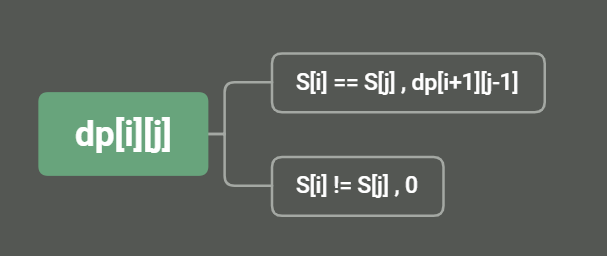
再来看看动态规划满足的前提条件有三种：
-
最优子结构，在回文子串的两边加上同一个字符依旧可以组成一个新的回文子串，因此后一种状态可以通过上一个状态推导出来，即问题的最优解所包含的子问题的解也是最优的。举个例子：一个国家有一个最强士兵(最优解)，那么这个士兵一定是所在军营里最强的士兵。
-
有边界，遍历的时候是从两个端点开始，因此j的值始终比i大，所以推到出边界为j - i >= 0;
-
重叠子问题，即子问题之间是不独立的，一个子问题在下一阶段决策中可能被多次用到。也就是说，如果i和j中的子串不是回文子串，就算S[i] == S[j]其状态也应该为0。
最后代码如下：
public static String longestPalindrome(String s) { int len = s.length(); if (len <= 1) return s; boolean[][] dp = new boolean[len][len]; //初始化边界 for (int i=0;i<len;i++) { dp[i][i] = true; } char[] arr = s.toCharArray(); int max = 1; //至少要截取一个字符串 int startIndex = 0; for(int j = 1;j<len;j++) { for(int i=0;i<j;i++) { if(arr[i] != arr[j]) { dp[i][j] = false; }else { if(j-i < 2) { dp[i][j] = true; }else { dp[i][j] = dp[i+1][j-1]; } } if(dp[i][j] && j-i+1 > max) { max = j-i+1; startIndex = i; } } } return s.substring(startIndex, startIndex+max); }
解题字符串"abbacb"的二维状态数组如下
提交答案后发现：
执行的时长还是很高，那有没有更好的解题方案呢？这时候就介绍另一种解题方法
中心扩散法
class Solution { public static String longestPalindrome(String s) { if (s == null || s.length() == 0) { return ""; } // 保存起始位置，测试了用数组似乎能比全局变量稍快一点 int[] range = new int[2]; char[] str = s.toCharArray(); for (int i = 0; i < s.length(); i++) { // 把回文看成中间的部分全是同一字符，左右部分相对称 // 找到下一个与当前字符不同的字符 i = findLongest(str, i, range); } return s.substring(range[0], range[1] + 1); } public static int findLongest(char[] str, int low, int[] range) { // 查找中间部分 int high = low; while (high < str.length - 1 && str[high + 1] == str[low]) { high++; } // 定位中间部分的最后一个字符 int ans = high; // 从中间向左右扩散 while (low > 0 && high < str.length - 1 && str[low - 1] == str[high + 1]) { low--; high++; } // 记录最大长度 if (high - low > range[1] - range[0]) { range[0] = low; range[1] = high; } return ans; } }
程序会通过for循环遍历所有字符，然后调用findLongest方法，但是在该方法中只需要往左右扩散，因此在长的字符串中进行遍历，其效率会高于动态规划的解题方法。
其核心思路是找到回文子串的中间部分，然后在向左右进行比较，并记录最大长度的回文子串。
这个方法简直比动态规划快了近54倍！
