HGAME2020 Week2 Writeup
我太南了.jpg
Crypto - Verification_code
题目:
本周的签到题 XP
nc 47.98.192.231 25678
还有一段服务端的脚本
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
import socketserver
import os, sys, signal
import string, random
from hashlib import sha256
from secret import FLAG
class Task(socketserver.BaseRequestHandler):
def _recvall(self):
BUFF_SIZE = 2048
data = b''
while True:
part = self.request.recv(BUFF_SIZE)
data += part
if len(part) < BUFF_SIZE:
break
return data.strip()
def send(self, msg, newline=True):
try:
if newline: msg += b'\n'
self.request.sendall(msg)
except:
pass
def recv(self, prompt=b'> '):
self.send(prompt, newline=False)
return self._recvall()
def proof_of_work(self):
random.seed( os.urandom(8) )
proof = ''.join([ random.choice(string.ascii_letters+string.digits) for _ in range(20) ])
_hexdigest = sha256(proof.encode()).hexdigest()
self.send(str.encode( "sha256(XXXX+%s) == %s" % (proof[4:],_hexdigest) ))
x = self.recv(prompt=b'Give me XXXX: ')
if len(x) != 4 or sha256(x+proof[4:].encode()).hexdigest() != _hexdigest:
return False
return True
def handle(self):
signal.alarm(60)
if not self.proof_of_work():
return
self.send(b'The secret code?')
_code = self.recv()
if _code == b'I like playing Hgame':
self.send(b'Ok, you find me.')
self.send(b'Here is the flag: ' + FLAG)
self.send(b'Bye~')
else:
self.send(b'Rua!!!')
self.request.close()
class ThreadedServer(socketserver.ThreadingMixIn, socketserver.TCPServer):
pass
class ForkedServer(socketserver.ForkingMixIn, socketserver.TCPServer):
pass
if __name__ == "__main__":
HOST, PORT = '0.0.0.0', 1234
server = ForkedServer((HOST, PORT), Task)
server.allow_reuse_address = True
server.serve_forever()
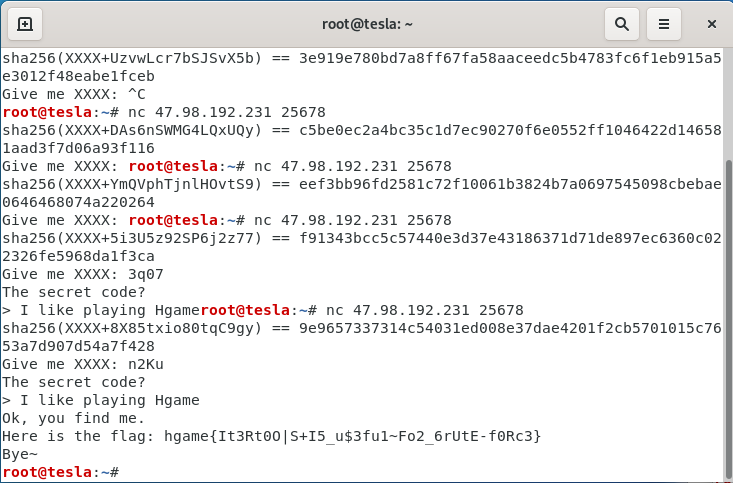
先直接nc建立连接,返回结果如下
root@tesla:~/桌面/hg# nc 47.98.192.231 25678
sha256(XXXX+ggsSLHtrFoRrIeCk) == 4e5da0bdb510375747dd0bd1f1c18befee4d850c09624636c5daa1c0e7595249
Give me XXXX:
题意应该是找对应的XXXX填上去就行了
由服务端的string.ascii_letters+string.digits可知XXXX的每个字符只有62种可能,因此直接爆破应该可行
然而实际操作的时候有一个问题,每一次nc建立连接得到的结果都不一样,而且连上服务器之后只有60秒的时间找到XXXX,然而我在电脑上直接跑一轮暴力验证很容易超时
之后在网上找了一下python多线程和多进程的教程,把时间缩短了一些,基本就能过了
脚本如下:
import string,sys
from hashlib import sha256
from multiprocessing import Process
table = (string.ascii_letters + string.digits).encode()
prefix = [string.ascii_lowercase.encode()[0:13],string.ascii_lowercase.encode()[13:26],string.ascii_uppercase.encode()[0:13],string.ascii_uppercase.encode()[13:26],string.digits.encode()]
def task(index,c,part):
for i in prefix[index]:
for j in table:
for k in table:
for l in table:
raw = i.to_bytes(1, 'big')
raw += j.to_bytes(1, 'big')
raw += k.to_bytes(1, 'big')
raw += l.to_bytes(1, 'big')
raw += part
if sha256(raw).hexdigest().encode() == c:
print(raw)
if __name__ == '__main__':
c = input().encode()
part = input().encode()
for i in range(5):
p=Process(target=task,args=(i,c,part))
p.start()
最终flag:hgame{It3Rt0O|S+I5_u$3fu1~Fo2_6rUtE-f0Rc3}
后记:
最初想到的优化方法是使用多线程,但是经过测试多线程穷举完所有字符的速度反而比单线程慢(后来得知可能是GIL的问题),于是改用多进程执行,速度就提上来了
flag当中提到的itertools是python中操作迭代对象的一个模块,应该可以用来替换脚本当中的嵌套for,等有空去试一下
这道题不一定要用多进程来优化,添加与服务器直接交互的功能也能有效提升解题速度,或者是用单进程手动交互的脚本多试几次,运气好的话也能在60秒内解出来
Crypto - Remander
题目:
烤个孙子
还有加密脚本:
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
from Crypto.Util import number
from secret import msg
assert 256 < len(msg) < 384
p, q, r = [number.getPrime(1024) for _ in range(3)]
# p = 94598296305713376652540411631949434301396235111673372738276754654188267010805522542068004453137678598891335408170277601381944584279339362056579262308427544671688614923839794522671378559276784734758727213070403838632286280473450086762286706863922968723202830398266220533885129175502142533600559292388005914561
# q = 150088216417404963893679242888992998793257903343994792697939121738029477790454833496600101388493792476973514786401036309378542808470513073408894727406158296404360452232777491992630316999043165374635001806841520490997788796152678742544032835808854339130676283497122770901196468323977265095016407164510827505883
# r = 145897736096689096151704740327665176308625097484116713780050311198775607465862066406830851710261868913835866335107146242979359964945125214420821146670919741118254402096944139483988745450480989706524191669371208210272907563936516990473246615375022630708213486725809819360033470468293100926616729742277729705727
m = number.bytes_to_long(msg)
e = 65537
for prime in [p, q, r]:
print( pow(m, e, prime) )
# 78430786011650521224561924814843614294806974988599591058915520397518526296422791089692107488534157589856611229978068659970976374971658909987299759719533519358232180721480719635602515525942678988896727128884803638257227848176298172896155463813264206982505797613067215182849559356336015634543181806296355552543
# 49576356423474222188205187306884167620746479677590121213791093908977295803476203510001060180959190917276817541142411523867555147201992480220531431019627681572335103200586388519695931348304970651875582413052411224818844160945410884130575771617919149619341762325633301313732947264125576866033934018462843559419
# 48131077962649497833189292637861442767562147447040134411078884485513840553188185954383330236190253388937785530658279768620213062244053151614962893628946343595642513870766877810534480536737200302699539396810545420021054225204683428522820350356470883574463849146422150244304147618195613796399010492125383322922
这题一开始找不到下手的地方,之后校内群里面出题人给了相关资料,结合题目的提示,大概知道是在考中国剩余定理
然而得到m ^ e mod M(M=p * q * r)的值后就无从下手了,想试着直接开e次方根但由于mod M的原因无法求解,感觉m ^ e mod M和题目中直接给出的m ^ e mod p的值似乎没有什么区别,因此一直拖到ddl前一天都没碰这道题
后来回想起week1中考RSA的题目当中也有pow(m, e, prime)和e,进一步思考,破解RSA的难点就在于分解公钥中的n(本题中的M),而n在本题中已经可以被分解为p、q和r,因此把e当作公钥结合p、q和r即可算出私钥,用RSA解密的流程即可得到明文m
在搜索过程当中还了解到,RSA当中用到的欧拉函数原始公式为euler(x)=x * (1-1/p1) * (1-1/p2) * (1-1/p3) * (1-1/p4) * … * (1-1/pn),其中p1,p2……pn为x的所有不重复素因数,因为RSA算法当中的n只有p、q两个素因子,代入公式即得euler(n)=(p-1)(q-1)。同理,本题中n(M)只有p、q和r三个素因子,代入公式可得euler(M)=(p-1)(q-1)(r-1)
最终的解密脚本如下:
import math, gmpy2
from gmpy2 import mpz
# 导入同余式组的除数m与余数a
a = []
a.append(mpz(78430786011650521224561924814843614294806974988599591058915520397518526296422791089692107488534157589856611229978068659970976374971658909987299759719533519358232180721480719635602515525942678988896727128884803638257227848176298172896155463813264206982505797613067215182849559356336015634543181806296355552543))
a.append(mpz(49576356423474222188205187306884167620746479677590121213791093908977295803476203510001060180959190917276817541142411523867555147201992480220531431019627681572335103200586388519695931348304970651875582413052411224818844160945410884130575771617919149619341762325633301313732947264125576866033934018462843559419))
a.append(mpz(48131077962649497833189292637861442767562147447040134411078884485513840553188185954383330236190253388937785530658279768620213062244053151614962893628946343595642513870766877810534480536737200302699539396810545420021054225204683428522820350356470883574463849146422150244304147618195613796399010492125383322922))
m = []
m.append(mpz(94598296305713376652540411631949434301396235111673372738276754654188267010805522542068004453137678598891335408170277601381944584279339362056579262308427544671688614923839794522671378559276784734758727213070403838632286280473450086762286706863922968723202830398266220533885129175502142533600559292388005914561))
m.append(mpz(150088216417404963893679242888992998793257903343994792697939121738029477790454833496600101388493792476973514786401036309378542808470513073408894727406158296404360452232777491992630316999043165374635001806841520490997788796152678742544032835808854339130676283497122770901196468323977265095016407164510827505883))
m.append(mpz(145897736096689096151704740327665176308625097484116713780050311198775607465862066406830851710261868913835866335107146242979359964945125214420821146670919741118254402096944139483988745450480989706524191669371208210272907563936516990473246615375022630708213486725809819360033470468293100926616729742277729705727))
# 使用中国剩余定理,得到的res即为m ^ e mod M
M = mpz(1)
res=mpz(0)
for i in m:
M *= i
for i in range(len(m)):
Mi = mpz(1)
for j in m:
if (j != m[i]):
Mi*=j
ti = gmpy2.invert(Mi, m[i])
res += a[i] * ti * Mi
res %= M
# 求欧拉函数euler(M)
phi = mpz(1)
for i in m:
phi*=i-1
# 求私钥,明文
inv = gmpy2.invert(65537, phi)
res = pow(res, inv, M)
print(str(int(res).to_bytes(384,'big'),'utf8'))
获得的明文如下:
1hAyuFoOUCamGW9BP7pGKCG81iSEnwAOM8x
********** DO NOT GUESS ME ********
hg In number theory,
am the Chinese
e{ remainder theorem
Cr states that if one
T_ knows the
w0 remainders of the
Nt Euclidean division
+6 of an integer n
Ot by several
h3 integers, then
R_ YOU CAN FIND THE
mE FLAG, ;D
!!
!}
********** USE YOUR BRAIN *********
cbl8KukOPUvpoe1LCpBchXHJTgmDknbFE2z
最终flag:hgame{CrT_w0Nt+6Oth3R_mE!!!}
Crypto - Inv
题目:
Does python "bytes" object have inverse?
还有加密脚本:
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
import gmpy2
from secret import Sbox, flag
assert set(range(256)) == set(Sbox)
assert flag.startswith(b'hgame{') and flag.endswith(b'}')
def Subs(S, X):
return bytes([ S[x] for x in X ])
def Mul(A, B):
assert len(A)==len(B)
return Subs(A, B)
def Pow(X, E):
Y = X
E = bin(E)[3:]
for e in E:
Y = Mul(Y, Y)
if e=='1':
Y = Mul(X, Y)
return Y
s = bytes(Sbox)
print( Pow(s, 595) )
print( Pow(s, 739) )
print( Subs(s, flag) )
# b'\xc8&\xc1E\xbe*\xc5\x84\xdb1\x05\x9b\xc0\xf2\xac/\x0b0\x8d\'\xc2b\x89\x93\xa6\xcd\xe1\x1b\xf4H\xffa\x90A\xf7,(\xea?\xa8\xa0\x8b\xf1\xf9"X\n\x86fj\x074\x7fBO\xd4F\xbd\xe6\xd9\xa7\xaf\x8a\x8c\xde\xab;!PT\x15)+w\xbc\x00>\xc6g\xc3\x85=9K\xb6<\xb7x\xaeUG\x83vk\xa9\xf6{\x03Y\x87\x14e\xfd\xed@i\xcc.\xd1\xebo\x106\xe2\xe7\xd7\xeeu\x9e\xfe\x95^R\xfb8\x04\xb4S\x16\xe0\xad\xd8\x98n\xca\xe4\xdd\xd2\xc7\x99l\xb3\\2L\xa3\x1d:_\x12\xb87\x17\x01\xb1#~q\x1c\t\xe8\xdar\xef\xcb\x0c\xe5\x80\xdf\xc9y\x0e`\xe9\x94\xd0\xcfW\x1f5\xf5h\xbf\xba\x91\xb9d\xfcM\x81\xec\x88\xb2c\x9f\xa4J|\xd3m\xd6s\xd5\x92\x9d\x9a3\xa2\xb5\xfa\x19N\xa1\x82][\xf8\x06\x13\xdcC\x1e\x1a\xaa\xc4tz\x08\x8f%$D\xbb\x97 \xce\x96V\xe3\x02I\x18\x11\x0f\r\xf3p\x8e\xa5Z-\xf0}\xb0Q\x9c'
# b'U\x17\x8aE\xa6\x19\xab\x7fd0\xd2)\xc0\xae\xcc/G_\xe3\'\r\xfb\xaf\x00\xb1hgi-\xc1\xffa\x8d\t&\x99k\x95\x93\xa8.\x07\xcd\x87\x01\xe8\x89\x86\xf6f48F\xdc\x96\xd4`P\xd6!\xfe\xc4B:\xd31C\x9f\x1dT{2c9\x0bY5#\xf7\xb8H\xe0Db\xb6wv\xe1\xbbI\x8f\x83l\x80\xa9\x04q\x03\xf0m\xf4\x1bp\x8e\xc6u\xfd\x16$\x06\xf9Z\xec\xa2\xcb\xd7V\xb9\xd1\xbdt^\xe7\xe2\xac\x18\xb4\x15=n\xad\xd8S+\xca\xeb\xdd\xd0;\x84\xe6\x08\x8c3\xb3\x90\x02\xc8}\xee\xea7K\x98\xde\x8b~\xcf\xfa\x11\n\xda\xa4L\xa3\x0cWQ\xdf\xc9yj\x9d\xe9\xfcJO\x1a\x1f\xdb\xf5M\xbf\x9e e\x1c*\x9b\x85\xe5\x88\xb2\xc7\xf2\x91\x10\x0e,\xd9<s\xd5\xef\xb0@|\xc3\xbc(\xb5"\xa1\x82\xa7[\xf8A\x13\x14\xc2\x1eN\xaao\xedr\xba\xcex]\x92\x05\x97\x12\xc5%\\\xb7>R\x9a\x94\x0fX\xf3\xbe?\xa5\xe4\xa0z\xf16\x81\x9c'
# b"\\-\xa5{\xb9\x85J @\xfa\x91\x0b\x88\r4I\x7f\xb9\xe5\r\xc0\x84\x8f\xa6\xc0i\xb0\xa4\x1b\x8fIw\x84'\xa2\xa4\x00\x91\x87\x10\r\\\x8c\x12'
基本上一整周都在做这道题,但其实是在week2ddl的前一个小时才找到了突破口
第一阶段
一开始先是分析Pow、Mul和Subs三个函数,在一番瞎折腾后发现Mul函数满足交换律(x)和结合律(未证明,只通过部分数据进行了验证)
之后分析Pow函数,根据E = bin(E)[3:]去计算595和739的二进制表示,结果如下:
595(10)=1001010011(2)
739(10)=1011100011(2)
发现1010011和1100011极其相似,尝试以此为突破口求解,无果
第二阶段
结合三个函数的名字以及Mul函数的性质,猜测Pow相当于求次方,而Mul相当于乘法
Pow整体看上去与快速幂十分相似,但是其从高位到低位的顺序和常见快速幂算法中从低位到高位的顺序不同,况且[3:]应该会丢失掉指数的高三位(其实不会),怀疑这个Pow是针对于Subs函数而写的,并没有通用性
不过验证方法也很简单,把Subs的函数体改为return S * X,然后对数字调用Pow函数即可。验证发现Pow函数的运算结果和正常求次方函数的结果居然是一致的?
对Pow函数进行调试分析,有了一些新发现。以指数595为例,脚本当中的bin()函数返回的结果并不是想象中的1001010011,而是0b1001010011,从索引为3的位置切片得到的结果E应该是001010011(被去掉的部分总是0b1)。而len(E)=9即为循环的次数,对Y进行len(E)次平方操作后即可得到指数最高位(1000000000)对应的因式(2 ^ 9),与此同时,在第i次循环中遇到的“1”位于指数二进制表示的第len(E)-i+1位,经过len(E)-i次循环后即可得到对应的因式(2 ^ (len(E)-i))),整个运算与常见快速幂算法其实是雷同的
根据上述分析,本题已知针对于bytes的类乘法运算和求次方运算,以及s ^ 595,s ^ 739和s * flag的值,理论上需要求出s,并通过s求出flag
如果s与flag都是数字那么本题就十分简单了,对s ^ 595直接开595次方得到s,然后用flag/s即可得到结果。然而本题中并没有给出针对bytes的开方运算或者类除法运算。尝试了一下,似乎通过已知的Mul函数和Pow函数也无法构造出开方运算和类除法运算
第三阶段
整理了一下之前的思路,不需要直接构造出开方运算,只要能构造出类除法运算那么这题也能够解出来
结合此题的题目描述,准确来说现在需要找到的是关于S的逆元T,也就是S ^ (-1),使得S * T=S * S ^ (-1)=1
这当中还有一个问题,“1”在这里对应的bytes是什么?根据数字1的性质,设“1”bytes为E,E应该满足Mul(X,E)=X(类似于矩阵当中的单位矩阵)。经过一些较短bytes的实验,“1”对应的是b'\x00\x01\x02\x03……'这样的与X等长的的bytes
在此期间校内群里面学长给出了这题的相关资料,并且提到了这题与共模攻击有关。因为求逆心切,以为这段资料可以用来求逆,然而发现资料当中甚至涉及到新运算mod,进一步搜索有关共模攻击的内容,发现使用共模攻击时也需要用到逆元
第四阶段
原本打算放弃这道题目,但在接近week2ddl时决定还是争取一下
因为c1=Pow(s, 595)和c2=Pow(s, 739)的长度均为256,结合set(range(256)) == set(Sbox),猜测s以及s的幂均为'\x00' ~ '\xff'的某种排列
一开始脑子迷糊了想直接爆破出c1的逆元,通过签到题提示的itertools很快构建出了爆破脚本。但在爆破了将近10分钟后突然意识到了爆破涉及的运算量,于是放弃了直接爆破的操作
抱着试试看的心态对几个长度较短的bytes进行爆破求逆元,并尝试观察逆元与原bytes的关系
获得的几组数据如下:
b'\x06\x02\x00\x05\x04\x03\x07\x01'
(2, 7, 1, 5, 4, 3, 0, 6)
b'\x01\x07\x00\x05\x02\x06\x03\x04'
(2, 0, 4, 6, 7, 3, 5, 1)
b'\x00\x02\x04\x01\x03\x06\x05\x07'
(0, 3, 1, 4, 2, 6, 5, 7)
观察得到以下规律:
设原bytes为S,其逆元为T,则对于i ∈ range(len(S)),总有T[S[i]]=i
由此构建出求逆函数Inv()如下:
def Inv(S):
l=len(S)
e = list(range(l))
res = list(range(l))
pre=list(S)
for i in range(l):
res[pre[i]]=e[i]
return bytes(res)
之后用学长说的共模攻击求解。题目中虽然没有提到公共模数n,但是我们可以假设n=595 * 739 * x,x的值非常大以至于运算过程中是否对n取模不影响结果。这样在形式上就满足RSA的共模攻击了。具体实施的时候参考了这篇文章
解题代码如下:
def Subs(S, X):
return bytes([S[x] for x in X])
def Mul(A, B):
return Subs(A, B)
def Pow(X, E):
Y = X
E = bin(E)[3:]
for e in E:
Y = Mul(Y, Y)
if e=='1':
Y = Mul(X, Y)
return Y
def Inv(S):
l=len(S)
e = list(range(l))
res = list(range(l))
pre=list(S)
for i in range(l):
res[pre[i]]=e[i]
return bytes(res)
c1=b'\xc8&\xc1E\xbe*\xc5\x84\xdb1\x05\x9b\xc0\xf2\xac/\x0b0\x8d\'\xc2b\x89\x93\xa6\xcd\xe1\x1b\xf4H\xffa\x90A\xf7,(\xea?\xa8\xa0\x8b\xf1\xf9"X\n\x86fj\x074\x7fBO\xd4F\xbd\xe6\xd9\xa7\xaf\x8a\x8c\xde\xab;!PT\x15)+w\xbc\x00>\xc6g\xc3\x85=9K\xb6<\xb7x\xaeUG\x83vk\xa9\xf6{\x03Y\x87\x14e\xfd\xed@i\xcc.\xd1\xebo\x106\xe2\xe7\xd7\xeeu\x9e\xfe\x95^R\xfb8\x04\xb4S\x16\xe0\xad\xd8\x98n\xca\xe4\xdd\xd2\xc7\x99l\xb3\\2L\xa3\x1d:_\x12\xb87\x17\x01\xb1#~q\x1c\t\xe8\xdar\xef\xcb\x0c\xe5\x80\xdf\xc9y\x0e`\xe9\x94\xd0\xcfW\x1f5\xf5h\xbf\xba\x91\xb9d\xfcM\x81\xec\x88\xb2c\x9f\xa4J|\xd3m\xd6s\xd5\x92\x9d\x9a3\xa2\xb5\xfa\x19N\xa1\x82][\xf8\x06\x13\xdcC\x1e\x1a\xaa\xc4tz\x08\x8f%$D\xbb\x97 \xce\x96V\xe3\x02I\x18\x11\x0f\r\xf3p\x8e\xa5Z-\xf0}\xb0Q\x9c'
c2=b'U\x17\x8aE\xa6\x19\xab\x7fd0\xd2)\xc0\xae\xcc/G_\xe3\'\r\xfb\xaf\x00\xb1hgi-\xc1\xffa\x8d\t&\x99k\x95\x93\xa8.\x07\xcd\x87\x01\xe8\x89\x86\xf6f48F\xdc\x96\xd4`P\xd6!\xfe\xc4B:\xd31C\x9f\x1dT{2c9\x0bY5#\xf7\xb8H\xe0Db\xb6wv\xe1\xbbI\x8f\x83l\x80\xa9\x04q\x03\xf0m\xf4\x1bp\x8e\xc6u\xfd\x16$\x06\xf9Z\xec\xa2\xcb\xd7V\xb9\xd1\xbdt^\xe7\xe2\xac\x18\xb4\x15=n\xad\xd8S+\xca\xeb\xdd\xd0;\x84\xe6\x08\x8c3\xb3\x90\x02\xc8}\xee\xea7K\x98\xde\x8b~\xcf\xfa\x11\n\xda\xa4L\xa3\x0cWQ\xdf\xc9yj\x9d\xe9\xfcJO\x1a\x1f\xdb\xf5M\xbf\x9e e\x1c*\x9b\x85\xe5\x88\xb2\xc7\xf2\x91\x10\x0e,\xd9<s\xd5\xef\xb0@|\xc3\xbc(\xb5"\xa1\x82\xa7[\xf8A\x13\x14\xc2\x1eN\xaao\xedr\xba\xcex]\x92\x05\x97\x12\xc5%\\\xb7>R\x9a\x94\x0fX\xf3\xbe?\xa5\xe4\xa0z\xf16\x81\x9c'
flag=b'\\-\xa5{\xb9\x85J @\xfa\x91\x0b\x88\r4I\x7f\xb9\xe5\r\xc0\x84\x8f\xa6\xc0i\xb0\xa4\x1b\x8fIw\x84\'\xa2\xa4\x00\x91\x87\x10\r\\\x8c\x12'
s1 = -272
s2 = 219
invc1 = Inv(c1)
s = Mul(Pow(invc1, -s1), Pow(c2, s2))
invs = Inv(s)
print(Subs(invs,flag))
当中的s1,s2是直接在WolframAlpha当中输入595x+739y=1求解的
因为Mul函数要求两个参数等长,所以最后求flag的时候用的是Subs函数,并且经尝试invs必须作为第一个参数,否则会提示下标过界(此时Subs函数不满足交换律)
原始脚本中提供的Subs(s,flag)为
b"\\-\xa5{\xb9\x85J @\xfa\x91\x0b\x88\r4I\x7f\xb9\xe5\r\xc0\x84\x8f\xa6\xc0i\xb0\xa4\x1b\x8fIw\x84'\xa2\xa4\x00\x91\x87\x10\r\\\x8c\x12'
直接用于解密会出错,尝试将其改为字符串,发现无法进行运算,后经过微调(前后引号匹配,中间的单引号加转义字符),改为
b'\\-\xa5{\xb9\x85J @\xfa\x91\x0b\x88\r4I\x7f\xb9\xe5\r\xc0\x84\x8f\xa6\xc0i\xb0\xa4\x1b\x8fIw\x84\'\xa2\xa4\x00\x91\x87\x10\r\\\x8c\x12'
即可得到flag
最终flag:hgame{U_kN0w~tH3+eXtEnD-EuC1iD34n^A1G0rIthM}
后记:
其实也没有用扩展欧几里得算法求解(因为还是不太懂)(WolframAlpha万岁!!!)
写wp的时候结合资料来看整个题目,难点还是在于求逆,在完成求逆的函数之后,通过已知的s ^ 595,s ^ 739以及求逆得到的s ^ (-595),s ^ (-739)可以通过各种拼凑得到s ^ (-1),进而还原出flag
为什么可以凑出s ^ (-1)呢,因为由裴蜀(贝祖)定理可得,对于整数a,b,一定存在一对x,y ∈ Z,使得ax+by=gcd(a,b),本题中的595与739互质,也就是说找得到一组整数x,y使得595x+739y=1,进而可以得到s ^ (595x+739y)=(s ^ 595) ^ x * (s ^ 739) ^ y=s ^ 1,因此(s ^ 595) ^ (-x) * (s ^ 739) ^ (-y)=s ^ (-1)。观察式子不难发现这一组x,y必定是异号的,而求逆就是为了计算s的负指数次幂
换一个角度来想,如果出题人给出的是Pow(s,466),Pow(s,844)和Subs(Pow(s,2),flag)(存在gcd(466,844)=2),那么本题也应该可以求解(吧)
感觉这道题并没有利用到共模攻击当中模相同所带来的一系列性质,只是沿用了一下求解的部分过程
最后验证下来Mul函数不满足交换律,之前验证的时候直接用了s ^ 595和s ^ 739,所以误以为满足交换律
Misc - 所见即为假
题目:
真亦假,假亦真,真真假假,假假真真;
实亦虚,虚亦实,实实虚虚,虚虚实实。
ObjectNotFound给了你一个压缩包和一副对子,转身离开了。
打开压缩包发现里面有一张加密的图片
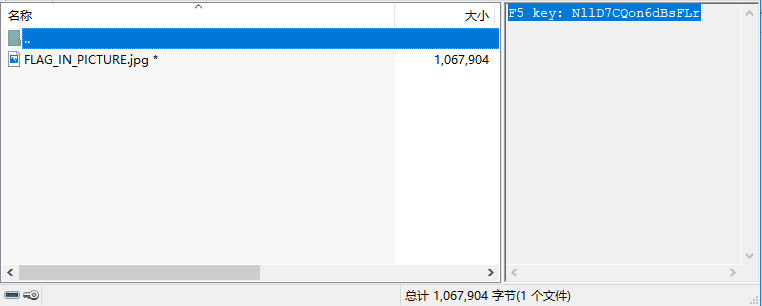
同时压缩包注释里面有以下内容:
F5 key: NllD7CQon6dBsFLr
以NllD7CQon6dBsFLr为密码打开压缩包,失败
把NllD7CQon6dBsFLr进行base64解码,得到一串非常奇怪的字符,猜测应该不是密码
后来想到题目中的对子,可能flag不在图片里面,而是以类似图种的方式隐藏在压缩文件头部,遂用16进制编辑器打开压缩包并和网上的zip包特征一一比对,发现文件头部和尾部与zip文件特征相同,于是排除了这种可能
不过在比对zip包特征时发现了一个异常情况,正常的加密zip文件头部应该是
50 4B 03 04 14 00 09 00
而题目压缩文件的头部是
50 4B 03 04 14 00 00 00
百度了一下,zip文件存在伪加密的情况,遇到这种文件通常只需要把文件中的
50 4B 01 02 3F 00 14 00 09 00
改为
50 4B 01 02 3F 00 14 00 00 00
即可(更改压缩源文件目录区的全局方式位标记)
经过上述修改后成功解压出了图片,按照网上的教程用stegsolve的各个功能跑了一遍,似乎没有发现什么东西(其实有东西)
怀疑出题人没有把flag放到图片里面,为了证实这一点,按照week1的方法用识图平台找到了原图,通过比较文件大小,确定出题人在图片上面动过手脚(题目图片大小大于原始图片大小),否定了这一猜测
用16进制编辑器打开两张图片,发现两张图片都有正常的jpg头部和尾部(FF D8和FF D9),但是题目图片的头部多了以下内容:
AJPEG Encoder Copyright 1998, James R. Weeks and BioElectroMech
之前用stegsolve的时候也看到了这段文字,但是没有意识到里面有问题,百度发现这是使用过基于F5算法的隐写软件的特征,结合zip包注释中的F5 key,基本确定这是图像隐写题
百度F5隐写的相关内容,在github上clone了一个相关工具,用对应的F5 key解码获得了以下内容
526172211A0701003392B5E50A01050600050101808000B9527AEA2402030BA70004A70020CB5BDC2D80000008666C61672E7478740A03029A9D6C65DFCED5016867616D657B343038375E7A236D737733344552746E46557971704B556B32646D4C505736307D1D77565103050400
看到里面只出现了大写字母和数字,怀疑是base32或者base16编码,经过测试发现base32解码失败(base32中只有A ~ Z,2 ~ 7和=),base16解码得到以下内容
b'Rar!\x1a\x07\x01\x003\x92\xb5\xe5\n\x01\x05\x06\x00\x05\x01\x01\x80\x80\x00\xb9Rz\xea$\x02\x03\x0b\xa7\x00\x04\xa7\x00 \xcb[\xdc-\x80\x00\x00\x08flag.txt\n\x03\x02\x9a\x9dle\xdf\xce\xd5\x01hgame{4087^z#msw34ERtnFUyqpKUk2dmLPW60}\x1dwVQ\x03\x05\x04\x00'
之前的题目当中总是出现Rua!而解码的结果却是Rar!,怀疑这串文本需要进一步解密,但是结果中直接出现了hgame{...},经过尝试这就是flag
最终flag:hgame{4087^z#msw34ERtnFUyqpKUk2dmLPW60}
后记:
百度得知52617221是rar文件头部的标志,正常操作应该是将F5解码的结果输出为二进制的RAR文件打开,得到含有flag的文本文件
Misc - 地球上最后的夜晚
题目:
农历一年中最后的夜晚马上就要来临了。
唔...“最后的夜晚”...这让我想起了去年春节前夕。
一个“上”字,区分开了名著《地球上最后的夜晚》,和毕赣导演的《地球最后的夜晚》。
一年了,ObjectNotFound手里的那本《地球上最后的夜晚》,还没有看完...
这道题总体来说难度不高。打开压缩包看到有一个pdf文件和另一个加密的压缩包,先尝试改后缀为zip以及用binwalk和strings搜索,无果。之后查资料得知pdf文件可用wbStego进行信息隐写,于是下载工具解密得到以下内容:
Zip Password: OmR#O12#b3b%s*IW
打开加密的压缩包,得到一个docx文件。先是找了一下文档当中的隐藏文字,没有结果。考虑到docx文件本质上是一个压缩包,于是改后缀名为zip并在压缩包内搜索,最后在\word\secret.xml当中找到了flag
最终flag:hgame{mkLbn8hP2g!p9ezPHqHuBu66SeDA13u1}
Misc - Cosmos的午餐
题目:
Cosmos做梦都想吃一次芽衣亲手做的午餐,边吃饭边左拥八重樱右抱希儿这种。
他在屏幕前对着图片做白日梦的样子恰巧被路过的ObjectNotFound看到了。
“唔...好香呀!”
“Cosmos!醒醒!别睡了!!起来做PWN了!!!”
PS: Cosmos经常往图片备注里塞东西。
压缩包里面有一个Wireshark的抓包文件和SSL的log文件
在看完上个星期的官方wp后,我大概掌握了pcapng文件的处理方法(然而接下来出了很多错)。同时包里面的SSL文件肯定不是白给,于是直接百度“wireshark ssl”,找到了分析pcapng中https包的方法
(编辑→首选项→Protocols→TLS(或者是SSL)当中指定SSL的log文件路径)
先在过滤器中输入http筛选所有的http包,在分组列表中按照大小排序,找到大小为8291的一个可疑包,通过查看Decrypted TLS数据发现末尾部分有Outgess with key.jpg,同时还有两个PK出现(zip文件标志),推测可以通过导出zip文件进行下一步操作,于是直接将Transport Layer Security→TLS segment data部分(大小为8208)导出为二进制文件,结果无法打开文件
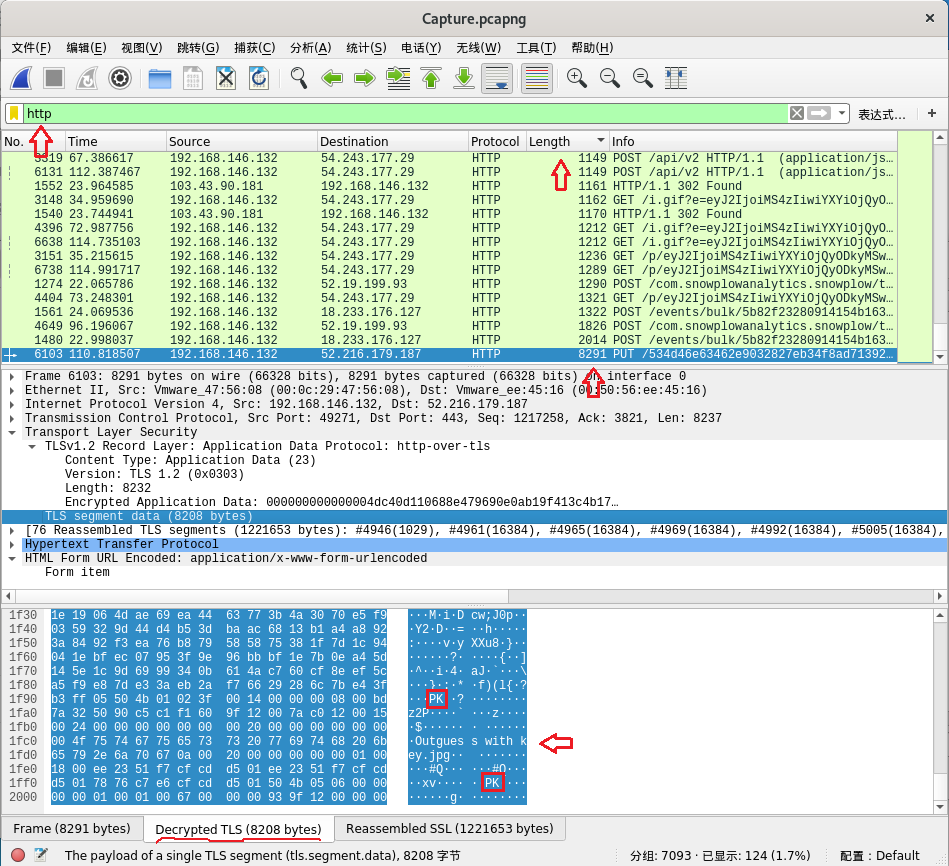
查看导出文件,发现缺少zip文件的头部特征,但是无论怎么补头都无法打开,考虑到week2应该不会出过于变态的补文件头题目,于是怀疑自己导出的文件有问题
后进入文件→导出对象→HTTP...,在HTTP对象列表中按照大小排序,找到大小为1220kB的文件,导出后成功作为zip文件打开,得到一张图片,结合题目提示和文件名,在图片备注中获得了用于解密的key:
gUNrbbdR9XhRBDGpzz
之后clone Outguess解密工具并编译安装,将图片解密得到一个网址
https://dwz.cn/69rOREdu
下载了一个叫ScanMe的压缩包,打开之后是一张被魔改过的二维码

直接扫描识别失败,根据图片上的小点来分析,应该需要把图上除HGAME和Vidar Logo以外的所有小点替换为大点才能够使扫码软件识别它
手动替换之后的结果如下(不会写脚本的痛)

扫码即可获得flag
最终flag:hgame{ls#z^$7j%yL9wmObZ#MKZKM7!nGnDvTC}
后记:
在成功获得flag后继续对原pcapng文件进行分析,发现封包中zip文件是被拆成若干个segments发送的,而在分组列表当中显示的包长度以及Decrypted TLS对应的大小似乎只与最后一个segment有关,第一次导出文件时只得到了zip文件的尾部(含有两个PK标记,但是缺少头部,文件大小也远小于实际zip文件大小)也可以说明这一点
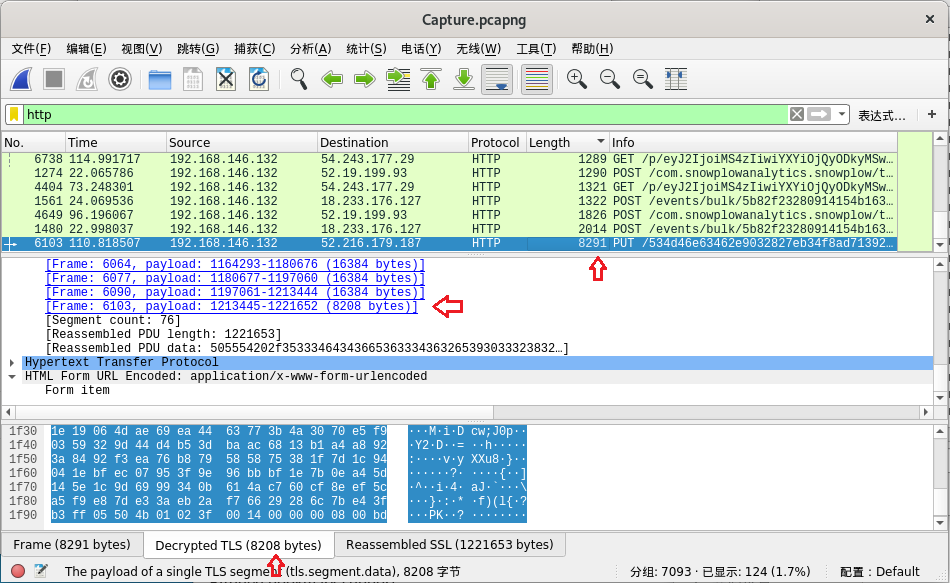
目前有个处理图片的简单思路:对图中每个9 * 9的区域进行识别,如果该区域只有中心的3 * 3为黑色而其余部分为白色,则将整个区域涂为黑色。因为二维码中间嵌入了Vidar Logo和HGAME的字样,其原始图片的容错率应该是比较高的,因此含有Vidar Logo和HGAME的部分即使没有被正确编码也不要紧。由于目前没怎么接触过python的图像处理功能,所以短时间内写不出脚本
第二次做CTF类的题目,感觉自己更菜了,做出来的题目只有1/4,而且用时太长
Crypto出题人Lurkrul大佬tql
2020.01.31






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列(二):开始使用ML.NET
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· C#/.NET/.NET Core优秀项目和框架2025年2月简报
· Manus爆火,是硬核还是营销?
· 终于写完轮子一部分:tcp代理 了,记录一下
· Qt个人项目总结 —— MySQL数据库查询与断言