USACO 2024 Feb bronze
挖个坑,今天晚上完成三篇手工翻译。awa
T1 Palindrome Game
赛时 100分
经典博弈论。手动枚举一下,很容易发现规律,当 S 为 10 的倍数时,先手输。
手动枚举需注意,不会证明你先别急,枚举要多,才能得出普遍规律(这个傻逼比赛刚开始一直打的是,当 S 为时 10 先手输)。
需要注意的是 S 的非常大。
T2 Milk Exchange
赛时 93.75分
简要题意,有一群奶牛,她们和相邻的人牛交换牛奶,但是奶牛拿不了那么多牛奶。有些牛奶可能在交换的过程中浪费了。求交换 m 轮后剩余的牛奶。
如果把奶牛们传牛奶的过程抽象一张图的话,如下图(以样例以为例子)。我们很容易可以发现 1 .当这张图是一条链时,牛奶不会浪费。 2. 当两个点单独形成环的时候,牛奶不会浪费。 3. 当两个点形成环且环链接着链时,牛奶会发成浪费。
需要注意:牛奶不是无限多的,数据范围。
赛时代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6;
int n,m,a[N],k[N],s=0;
int pre[N];
char c[N];
int work(int x,int last){
///if(pre[x]==last) return a[x];
if(x==-1) return 0;
return a[x]+work(pre[x],x);
}
signed main(){
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>c[i];
for(int i=1;i<=n;i++) cin>>a[i],s+=a[i];
memset(pre,-1,sizeof(pre));
for(int i=1;i<=n;i++){
if(c[i]=='L'){
if(pre[i]!=i-1) pre[i-1]=i;
k[i-1]++;
k[i]--;
}
if(c[i]=='R'){
if(pre[i]!=i+1) pre[i+1]=i;
k[i+1]++;
k[i]--;
}
}
if(pre[1]==0) pre[1]=n;
if(pre[n]==0) pre[n]=1;
k[n]+=k[0];
k[1]+=k[n+1];
int ans=0;
for(int i=1;i<=n;i++){
if(k[i]>0){
int maxx=work(i,0)-a[i];
k[i]*=m;
ans+=min(k[i],maxx);
}
}
cout<<s-ans;
return 0;
}
debug细节处理有误。
订正代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6;
int n,m,a[N],k[N],s=0;
int pre[N];
char c[N];
int work(int x,int last){
if(x==-1) return 0;
return a[x]+work(pre[x],x);
}
signed main(){
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>c[i];
for(int i=1;i<=n;i++) cin>>a[i],s+=a[i];
memset(pre,-1,sizeof(pre));
for(int i=1;i<=n;i++){
if(c[i]=='L'){
if(pre[i]!=i-1) pre[i-1]=i;
k[i-1]++;
k[i]--;
}
if(c[i]=='R'){
if(pre[i]!=i+1) pre[i+1]=i;
k[i+1]++;
k[i]--;
}
}
if(pre[0]==1) pre[n]=1;
if(pre[n+1]==n) pre[1]=n;
k[n]+=k[0];
k[1]+=k[n+1];
int ans=0;
for(int i=1;i<=n;i++){
if(k[i]>0){
int maxx=work(i,0)-a[i];
k[i]*=m;
ans+=min(k[i],maxx);
}
}
cout<<s-ans;
return 0;
}
T3 Maximizing Productivity
赛时分数 23.53分
题意感觉比较容易让人混淆,反正比赛的时候我是读了很多很多遍。
简要题意:已知
暴力的做法,很简单。每次询问都遍历一边,统计符合条件的 i 即可。时间复杂度 O(nQ) 。 1≤Q≤2⋅105 ,1≤N≤2⋅105 。这个数据范围显然是难以通过的。
考虑怎么优化。首先
以此我们可以根据
赛时代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e6;
int n,q,k[N];
int v,s,jsq;
struct code{
int c,t,k;
}a[N];
int main(){
scanf("%d%d",&n,&q);
for(int i=1;i<=n;i++) scanf("%d",&a[i].c);
for(int i=1;i<=n;i++) scanf("%d",&a[i].t);
for(int p=1;p<=q;p++){
scanf("%d%d",&v,&s);
jsq=0;
for(int i=1;i<=n;i++){
if(s+a[i].t>=a[i].c) continue;
jsq++;
}
if(jsq>=v) printf("YES\n");
else printf("NO\n");
}
return 0;
}
需要注意数据范围。
本文来自博客园,作者:Wh1sky,转载请注明原文链接:https://www.cnblogs.com/wh1sky/p/18022323

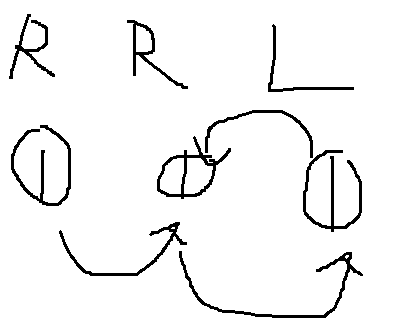


【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 微软正式发布.NET 10 Preview 1:开启下一代开发框架新篇章
· 没有源码,如何修改代码逻辑?
· NetPad:一个.NET开源、跨平台的C#编辑器
· PowerShell开发游戏 · 打蜜蜂
· 凌晨三点救火实录:Java内存泄漏的七个神坑,你至少踩过三个!