100 DP

- 2.20 数位dp

数位dp的求解的问题之一就是 [L,R]区间内有多少个满足限制条件的数。

对于这类问题，我们可以采用记忆化搜索来解决。

- 2.2 Bear and Bowling

DP思路，考虑前i个数选j个数的最大值，易得转移方程 \(f[i][j]=\max(f[i-1][j],f[i-1][j-1]+a[i]*j)\) 。

无后效性原则，最优子结构：对于前i个数已经选了j个数，无论如何第 i 个数贡献只能是 0 或者 a[i] *j。对当前状态的影响只有a[i]的数值，和选的个数。

空间的优化：二维压一维。
\(f[j]=\max(f[j],f[j-1]+a[i]*j)\)
因为当前的状态 f[j] 一定是由 f[j] f[j-1] 转移而来，所以我们在遍历的时候，可以使 j 从大到小便利，这样就不会使f[i-1]这一层数据还没转移就被覆盖。

- 1.25 P2340 USACO03FALL Cow Exhibition G

这是一道经典的dfs？背包？

首先看题目 n 头小牛，有情商和智商，选小牛，使得所有的小牛智商情商之和最大（并且不情商之和和智商之和要大于0）

看到题目我们肯定会想到经典的dfs模型，选与不选。这道题显然可以用dfs来解决，但是这个时间复杂度有些不尽人意。1≤N≤400，时间复杂度(2^n)。这根据这个选与不选的模型，我们很容易想到01背包。

本来根据这个思路，我想到设计 f[i][j1]=j1+j2 表示考虑到第i个，j1表示智商，j2表示情商。 \(f[i][j1]=min(f[i-1][j1],f[i-1][j1-a[i].f1]+a[i].f1+a[i].f2)\) 。按理来说这样是可以的，但是因为题目要考虑负数的问题，所以实际上的转移就会变得非常麻烦。而且既然f的第二维一以及记录了a[i].f1，真的需要把a[i].f1也记录吗？那到底要怎么操作呢？

看了题解后的启发\(f[j]=max(f[j],f[j-a[i].f1]+a[i].f2);\)

DFS

#include<bits/stdc++.h>
using namespace std;
const int N=405;
int n,ans=0,f[800010];
struct code{
	int f1,f2,s;
}a[N];

int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i].f1>>a[i].f2;
	}
	memset(f,0xc0c0c0c0,sizeof(f));
	f[400000]=0;
	for(int i=1;i<=n;i++){
		if(a[i].f1>0){
			for(int j=800000;j>=a[i].f1;j--){
				f[j]=max(f[j],f[j-a[i].f1]+a[i].f2);
			}
		}
		else{
			for(int j=0;j<=800000+a[i].f1;j++){
				f[j]=max(f[j],f[j-a[i].f1]+a[i].f2);
			}
		}
	}
	for(int j=400000;j<=800000;j++){
		if(f[j]>0) 
		ans=max(ans,j-400000+f[j]);	
	}
	cout<<ans;
	return 0;
}

DP

没看题解

#include<bits/stdc++.h>
using namespace std;
const int N=405;
int n,ans=0,f[N][100000];
struct code{
	int f1,f2,s;
}a[N];
int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i].f1>>a[i].f2;
	}
	memset(f,-1,sizeof(f));
	
	f[1][(a[1].f1<0) ? (-1*a[1].f1+400000) : (a[1].f1)]=a[1].f2+a[1].f1;
	if(!(a[1].f1<0||a[1].f2<0)) ans=max(ans,f[1][a[1].f1]);
	
	for(int i=1;i<=n;i++){
		for(int j=-400000;j<=400000;j++){
			int j1=j-a[i].f1,s=a[i].f1+a[i].f2;
			if(j<0) j=-1*j+40000;
			f[i][j]=max(f[i][j],f[i-1][j1<0 ? -1*j1+40000 : j1]+s);
			f[i][j]=max(f[i][j],f[i-1][j]+s);
		}
	}
	for(int j=0;j<=400000;j++){
		ans=max(ans,f[n][j]);	
	}
	cout<<ans;
	return 0;
}

看了题解

#include<bits/stdc++.h>
using namespace std;
const int N=405;
int n,ans=0,f[800010];
struct code{
	int f1,f2,s;
}a[N];

int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i].f1>>a[i].f2;
	}
	memset(f,0xc0c0c0c0,sizeof(f));
	f[400000]=0;
	for(int i=1;i<=n;i++){
		if(a[i].f1>0){
			for(int j=800000;j>=a[i].f1;j--){
				f[j]=max(f[j],f[j-a[i].f1]+a[i].f2);
			}
		}
		else{
			for(int j=0;j<=800000+a[i].f1;j++){
				f[j]=max(f[j],f[j-a[i].f1]+a[i].f2);
			}
		}
	}
	for(int j=400000;j<=800000;j++){
		if(f[j]>0) 
		ans=max(ans,j-400000+f[j]);	
	}
	cout<<ans;
	return 0;
}

- 1.23 P1103 书本整理

题目简化给定一个数列，和一个数字k，有k次机会将数列中的数字减一。求相邻差值之和最少。

其实如果考虑扔掉k本书，操作起来感觉非常的麻烦。如果考虑留下（n-k）书，再求差值是否会更简便呢？

f[i][j]=min(f[i][j],f[k][j-1]+abs(a[i]-a[k]));

考虑如何排书——
前i本书，选j本书。考虑摆在哪类书的下边。

- 1.178~1.19 P1564 膜拜

思路简述：考虑前i个人分配机房，需要的最小机房数。再根据题目要求（要么保证整个机房都是同一位神牛的膜拜者，或者两个神牛的膜拜者人数差不超过 m）设计状态转移方程。

f[i]=min(f[i],f[j]+1)(abs(s1-s2)<=m||s1t||s2t)
//t为i_{j+1段的人数，s1为i}j+1段膜拜牛1的人，s2为i~j+1段膜拜牛2的人

- 1.12 P3842 [TJOI2007] 线段

/*死掉的代码与死掉的思路
	f[i][j] 表示停在第i行，第j列，且完成改行的线段任务的最短路径
	f[i][j1]=min(f[i-1][j2]+cost,f[i][j1])
	cost为完成任务的话费，1<=j1<=n&&1<=j2<=n
但仔细思考后就会发现，cost很难求，并且没必要停留在非线段覆盖的点上*/
#include<bits/stdc++.h>
using namespace std;
const int N=2*1e4;
int n,l[N],r[N],f[N][N];
int ans=0x3f3f3f3f;
int work(int i,int j1,int j2){
	int cost=1;
	int a=l[i],b=r[i];
	int s=min(j1,j2),t=max(j1,j2);
	if(s<=a) cost+=abs(b-s)+abs(b-t);
	else if(s<=b) cost+=abs(s-a)+abs(b-a)+abs(b-t);
	else cost+=abs(s-a)+abs(t-a);
	return cost;
}
int main(){
	cin>>n;
	for(int i=1;i<=n;i++) cin>>l[i]>>r[i];
	
	memset(f,0x3f3f3f3f,sizeof(f));
	f[1][1]=0;
	for(int j=1;j<=n;j++){
		int cost=(j-1);
		if(j<=r[1]) cost+=(r[1]-j)*2;
		f[1][j]=cost;
	}
	for(int i=2;i<=n;i++){
		for(int j1=1;j1<=n;j1++){
			for(int j2=1;j2<=n;j2++){
				if(f[i][j1]>f[i-1][j2]){
					int tmp=f[i-1][j2]+work(i,j1,j2);
				//	if(f[i][j1]>tmp){
				///	cout<<i<<' '<<j1<<' '<<j2<<' '<<tmp<<' '<<work(i,j1,j2)<<endl;
				//	}
					f[i][j1]=min(f[i][j1],tmp);	
				}
				
			}
	////		cout<<f[i][j1]<<endl;
		///	if(i==n) ans=min(f[n][j1],ans);
		}
	}
///	cout<<ans;
	for(int j=1;j<=n;j++){
		ans=min(ans,f[n][j]);
	}
	cout<<ans;
	return 0;
}

思考简化掉一下无用的状态空间。
f[i][0/1]表示第i行的完成第i条线段，结束时站在左端点(0)右端点(1)的最优情况
下图是四种转移的情况。
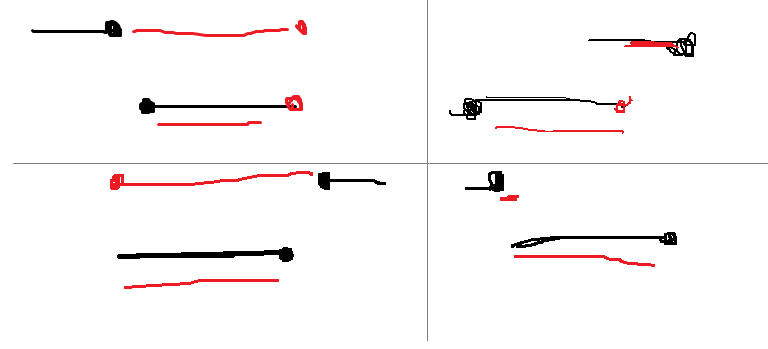
四种cost计算情况

- 1.11 P1095 [NOIP2007 普及组] 守望者的逃离

二维DP

\[f_{i,j}= \max \begin{cases} f_{{i-1},{j-4}} \\ f_{{i-1},{j}}+7 \\ f_{i,j+10}+60 \end{cases} \]

二维dp 代码记录

一维DP

因为题目要求最短的时间，最长的路程。所以如果能使用魔法就尽量使用魔法。但是如果只使用魔法的话，会发现最后的时间里恢复的能量值是不足以使用魔法的，那休息还不如走两步路呢。于是我们就想到用 \(f_i\) 来表示第i秒的走的的最长的路程。先处理好，如果只用魔法能走得最长路。在此基础上在处理走路的情况。
//不需要考虑先走路还是先用魔法的问题，因为无论顺序怎么样，到终点花费的时间是一样的。（无后效性）

#include<bits/stdc++.h>
using namespace std;
int m,s,t;
int f[1000006];
int main(){
	cin>>m>>s>>t;
	for(int i=1;i<=t;i++){
		if(m>=10){
			m-=10;
			f[i]=f[i-1]+60;
		}
		else{
			m+=4; f[i]=f[i-1];
		} 
	}
	for(int i=1;i<=t;i++){
		f[i]=max(f[i],f[i-1]+17);
		if(f[i]>=s){
			cout<<"Yes"<<endl<<i;
			return 0;
		}
	}
	cout<<"No"<<endl<<f[t];
	
	return 0;
}

贪心

贪心写法，烂尾了。。。

#include<bits/stdc++.h>
using namespace std;
int m,s,t;
int main(){
	cin>>m>>s>>t;
	int now=0;
	for(int i=1;i<=t;i++){
		if(m>=10){
			if(now+(m/10)*60>=s){
				while(now<s){
					now+=60;
					m/=10;
					i++;
					if(i==t) break;
				}
				cout<<"Yes"<<endl;
				cout<<i-1;
				return 0;
			}
			now+=min(m/10,t-i+1)*60;
			i+=m/10-1;
			m-=m/10*10;
		}
		else{
			if( ceil((s-now*1.0)/17)<(10-m)/4||
				( (ceil((s-now*1.0)/17)>t-i) &&(10-m)/4+(ceil(s-now*1.0)/60>t-i) ) ){
				now+=17;
				if(now>=s){
					cout<<"Yes"<<endl;
					cout<<i;
					return 0;
				}
			}
			else  m+=4;
		}
		cout<<i<<" "<<now<<" "<<m<<endl;
	}
	cout<<"No"<<endl;
	cout<<now;
	return 0;
}

posted @ 2024-01-25 09:23 Wh1sky 阅读(6) 评论(0) 编辑收藏举报

刷新页面返回顶部

Wh1sky's Blog