图论-分层图最短路

引言

——“分层图最短路”顾名思意，可以知道是在分层的图上跑最短路得算法。当我开始学习这个算法是，看到这个算法名，总有些雨里雾里的。什么是分层，为什么要分层，怎么分层？

概念

概念：分层图最短路的模型就是在最短路模型的基础上加上 \(k\) 个决策。这 \(k\) 个决策，并不会影响图得结构，只影响当前状态的代价。

最短路与分层图最短路

• 最短路模型：给定n个点m个条路，求从s出发到t的最短距离

• 分层图最短路模型：给定n个点m条路以及k个决策，再求出s到t的最短距离

方法

1. 直接构建 \(k+1\) 层平行的图

2. 多开一维记录决策信息

方法一 建立平行图

1. 建图

2. 处理 \(k\) 个决策：对于\(k\) 个决策，我们可以开 \(k\)层与初始图相同的图。不同图得跨越就是不同决策，我们根据题意建设不同平行层之间的联系。

3. 跑最短路。

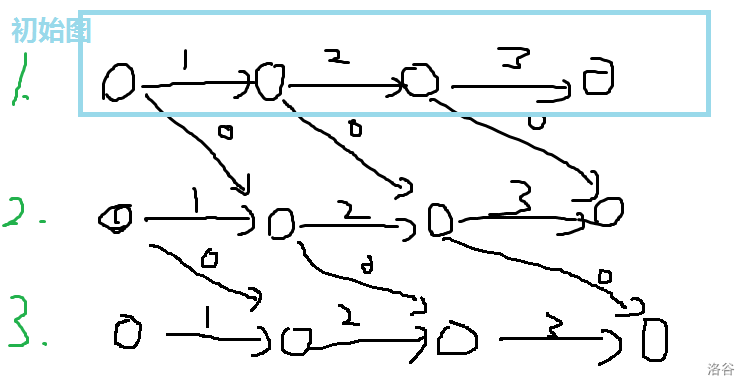
   例：给定一个图，有k次决策，可以使两点之间的边权变为0。 例子如图——

   

注意事项：因为有k层图，相当于初始图要存k遍，图的范围被扩大，时间和空间复杂度都要有所注意。

方法二 记录决策信息

还没学。

学习参考：

• 「学习笔记」分层图最短路 cyhyyds
• 分层图最短路 Eleven
• 图论学习笔记 - 分层图最短路问题（以飞行路线