二叉树的非递归遍历(先序、中序、后序和层序遍历)
[前文]
二叉树的非递归遍历有 先序遍历、中序遍历 、后续遍历 和 层序遍历。
非递归算法实现的基本思路:使用堆栈。而层序遍历的实现:使用队列。
如下图所示的二叉树:
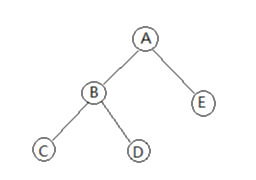
前序遍历顺序为:ABCDE (先访问根节点,然后先序遍历其左子树,最后先序遍历其右子树)
中序遍历顺序为:CBDAE (先中序遍历其左子树,然后访问很节点,最后中序遍历其右子树)
后续遍历顺序为:CDBEA (先后序遍历其左子树,然后后续其右子树,最后访问根节点)
层序遍历顺序为:ABECD (由上至下、从左到右遍历二叉树)
[准备]
1. 堆栈的存储结构和相关操作(具体见: 堆栈的定义与操作——顺序存储和链式存储)
2. 队列的存储结构和相关操作(具体见:队列的定义与操作——顺序存储和链式存储)
3. 建立二叉树。
1 typedef struct TreeNode *BinTree; 2 struct TreeNode { 3 char Data; 4 BinTree Left; 5 BinTree Right; 6 }; 7 8 BinTree CreateBinTree(BinTree T) 9 { 10 char c; 11 scanf("%c", &c); 12 if ( c != '#' ) { 13 T = (BinTree)malloc(sizeof(struct TreeNode)); 14 T->Data = c; 15 T->Left = CreateBinTree(T->Left); 16 T->Right = CreateBinTree(T->Right); 17 } 18 else { 19 T = NULL; 20 } 21 return T; 22 }
[实现]
1. 先序遍历
1 void PreOrderTraverse(BinTree BT) 2 { 3 BinTree T = BT; 4 Stack S = CreateStack(); /* 创建并初始化堆栈 */ 5 while ( T || !IsEmpty(S) ) { 6 while ( T ) { /* 一直向左并将沿途节点压入栈底 */ 7 printf("%c ", T->Data); /* 打印节点数据 */ 8 Push(S, T); 9 T = T->Left; 10 } 11 if ( !IsEmpty(S) ) { 12 T = Pop(S); /* 节点弹出堆栈 */ 13 T = T->Right; /* 转向右子树 */ 14 } 15 } 16 }
2.中序遍历
1 void InOrderTraverse(BinTree BT) 2 { 3 BinTree T = BT; 4 Stack S = CreateStack(); /* 创建并初始化堆栈 */ 5 while ( T || !IsEmpty(S) ) { 6 while ( T ) { /* 一直向左并将沿途节点压入栈底 */ 7 Push(S, T); 8 T = T->Left; 9 } 10 if ( !IsEmpty(S) ) { 11 T = Pop(S); /* 节点弹出堆栈 */ 12 printf("%c ", T->Data); /* 打印节点数据 */ 13 T = T->Right; /* 转向右子树 */ 14 } 15 } 16 }
3. 后序遍历
struct Node { BinTree BT; char Tag; }; typedef struct Node *PtrToNode; void PostOrderTraverse(BinTree T) { BinTree P = T; struct Node *PNode; Stack S = CreateStack(); while ( P || !IsEmpty(S) ) { // 遍历左子树 while ( P ) { PNode = (struct Node*)malloc(sizeof(struct Node)); PNode->BT = P; PNode->Tag = 'L'; // 第一次被标记 Push(S, PNode); P = P->Left; } // 栈不空 并且 栈顶元素 是第二次被标记 while ( !IsEmpty(S) && GetTop(S)->Tag == 'R' ) { PNode = Pop(S); printf("%c ", PNode->BT->Data); } if ( !IsEmpty(S) ) { PNode = GetTop(S); PNode->Tag = 'R'; // 第二次被标记 P = PNode->BT; P = P->Right; // 转向右子树 } } }
4. 层序遍历
1 void LevelOrderTraverse(BinTree BT) 2 { 3 Queue Q; 4 ElementType T; 5 6 if ( !BT ) return; // 若是空树则返回 7 8 Q = CreateQueue(); // 创建空队列 9 AddQ(Q, BT); 10 while ( !IsEmpty(Q) ) { 11 T = DeleteQ(Q); 12 printf("%c ", T->Data); 13 if ( T->Left ) AddQ(Q, T->Left); 14 if ( T->Right ) AddQ(Q, T->Right); 15 } 16 }


