<html>
Ellipsoid
Problem Description
Given a 3-dimension ellipsoid(椭球面)
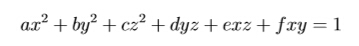
your task is to find the minimal distance between the original point (0,0,0) and points on the ellipsoid. The distance between two points (x1,y1,z1) and (x2,y2,z2) is defined as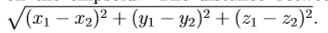
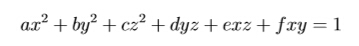
your task is to find the minimal distance between the original point (0,0,0) and points on the ellipsoid. The distance between two points (x1,y1,z1) and (x2,y2,z2) is defined as
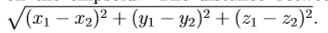
Input
There are multiple test cases. Please process till EOF.
For each testcase, one line contains 6 real number a,b,c(0 < a,b,c,< 1),d,e,f(0 ≤ d,e,f < 1), as described above. It is guaranteed that the input data forms a ellipsoid. All numbers are fit in double.
For each testcase, one line contains 6 real number a,b,c(0 < a,b,c,< 1),d,e,f(0 ≤ d,e,f < 1), as described above. It is guaranteed that the input data forms a ellipsoid. All numbers are fit in double.
Output
For each test contains one line. Describes the minimal distance. Answer will be considered as correct if their absolute error is less than 10-5.
Sample Input
1 0.04 0.01 0 0 0
Sample Output
1.0000000
Source
Recommend
hujie
题目大意:
求一个椭球面上的一个点到原点的最短距离。
解题思路:
模拟退火。不多解释了。
解题代码:
#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;
const double eps=1e-8;
const double INF=1e100;
const int offx[]={1,0,-1,0,1,-1,-1,1};
const int offy[]={0,1,0,-1,1,1,-1,-1};
double a,b,c,d,e,f;
double getAns(double x,double y){
double A=c,B=d*y+e*x,C=a*x*x+b*y*y+f*x*y-1.0;
double delta=B*B-4*A*C;
if(delta<0) return INF+10;
delta=sqrt(delta);
double z1=(-B+delta)/(2*A),z2=(-B-delta)/(2*A);
return min( sqrt(x*x+y*y+z1*z1) , sqrt(x*x+y*y+z2*z2) );
}
double tosolve(double sx,double sy){
double x=sx,y=sy,ans=getAns(sx,sy),step=1e6;
while(step>eps){
double sx=x,sy=y;
bool flag=false;
for(int i=0;i<8;i++){
double dx=x+offx[i]*step,dy=y+offy[i]*step;
double tmp=getAns(dx,dy);
if(tmp>=INF) continue;
if(tmp<ans){
ans=tmp;
flag=true;
sx=dx,sy=dy;
}
}
x=sx,y=sy;
if(!flag) step/=2;
}
return ans;
}
void solve(){
//cout<<tosolve(0,0)<<" "<<tosolve(sqrt(1.0/a),0)<<" "<<tosolve(0,sqrt(1.0/b))<<endl;
double ans=tosolve(0,0),tmp;
tmp=tosolve(sqrt(1.0/a),0);
if(tmp<ans) ans=tmp;
tmp=tosolve(-sqrt(1.0/a),0);
if(tmp<ans) ans=tmp;
tmp=tosolve(0,sqrt(1.0/b));
if(tmp<ans) ans=tmp;
tmp=tosolve(0,-sqrt(1.0/b));
if(tmp<ans) ans=tmp;
printf("%.7lf\n",ans);
}
int main(){
while(scanf("%lf%lf%lf%lf%lf%lf",&a,&b,&c,&d,&e,&f)!=EOF){
solve();
}
return 0;
}
版权声明:Tao Wang: 欢迎关注我的博客,本文为博主【炒饭君】原创文章,未经博主同意不得转载,Powered By Toyking.
举报
- 本文已收录于下面专栏:
相关文章推荐
-
uva 10228 - Star not a Tree?(模拟退火)
<a target="_blank" href="http://uva.onlinejudge.org/index.p
- 阿尔萨斯
- 2014-08-21 23:24
- 70
-
hdu 5017 Ellipsoid 模拟退火
Ellipsoid Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others) Total ...
- Ginray
- 2016-09-28 22:27
- 84
-
模拟退火算法介绍
模拟退火算法来源于固体退火原理,将固体加温至充分高,再让其徐徐冷却,加温时。固体内部粒子随温升变为无序状,内能增大,而徐徐冷却时粒子渐趋有序,在每一个温度都达到平衡态,最后在常温时达到基态,内能减为最小。依据Metropolis准则,粒子在温度T时趋于平衡的概率为e-ΔE/(kT),当中E为温度T时的内能,ΔE为其改变量,k为Bo
- wezly
- 2013-05-30 11:53
- 524
-
hdu 5017 ellipsoid 模拟退火
题目链接: #include #include #include using namespace std; #define INF 1e10 const double eps=1e-5...
- alpc_paul
- 2014-09-16 15:41
- 544
-
HDU 5017 Ellipsoid(模拟退火算法)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=5017

- piaocoder
- 2014-09-19 15:15
- 446
-
大白话解析模拟退火算法
优化算法入门系列文章文件夹(更新中): <p style="margin: 5px auto; font-family: Verdan
- wezly
- 2013-01-25 06:01
- 509
-
hdu 5017 Ellipsoid 模拟退火
Ellipsoid Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others) Tota...
- u012183589
- 2015-07-22 10:23
- 232
-
【转】模拟退火算法浅析
转自:http://www.cnblogs.com/heaad/archive/2010/12/20/1911614.html <p style="margin: 10px auto; font-family: Verdana, Geneva, Arial, Helvetica, sans-serif; font-s
- windshg
- 2012-11-14 15:43
- 219
-
HDU - 5017 Ellipsoid(模拟退火法)
Problem Description Given a 3-dimension ellipsoid(椭球面) your task is to find the minimal dist...
- u011345136
- 2014-10-04 14:37
- 1007
收藏助手
不良信息举报




0条评论