8-机器学习-逻辑回归项目案例
导入数据
import pandas as pd import matplotlib.pyplot as plt import numpy as np from pandas import DataFrame,Series %matplotlib inline states={'SeriousDlqin2yrs':'好坏客户', 'RevolvingUtilizationOfUnsecuredLines':'可用额度比值', 'age':'年龄', 'NumberOfTime30-59DaysPastDueNotWorse':'逾期30-59天笔数', 'DebtRatio':'负债率', 'MonthlyIncome':'月收入', 'NumberOfOpenCreditLinesAndLoans':'信贷数量', 'NumberOfTimes90DaysLate':'逾期90天笔数', 'NumberRealEstateLoansOrLines':'固定资产贷款量', 'NumberOfTime60-89DaysPastDueNotWorse':'逾期60-89天笔数', 'NumberOfDependents':'家属数量'} # index_col=0将原始数据第0列的数字去掉 data = pd.read_csv('./rankingcard.csv',index_col=0) data.head()
# 修改列索引将上边字典映射其中 data.rename(columns=states,inplace=True) data.head() # 1为不好的客户
去除重复的行数据
- 现实数据,尤其是银行业数据,可能会存在的一个问题就是样本重复,即有超过一行的样本所显示的所有特征都一样。
- 可以适当的恢复索引
# 查看是否有重复行数据 data.duplicated().sum() # 609 # 删除重复的数据 data.drop_duplicates(inplace=True) # 恢复行索引 data.index = range(data.shape[0]) data.shape # (149391, 11)
缺失数据处理
- 可以适当的恢复索引
# 查看哪列存在缺失数据 data.isnull().any(axis=0) 好坏客户 False 可用额度比值 False 年龄 False 逾期30-59天笔数 False 负债率 False 月收入 True 信贷数量 False 逾期90天笔数 False 固定资产贷款量 False 逾期60-89天笔数 False 家属数量 True dtype: bool # 查看缺失数据的个数 data.isnull().sum() 好坏客户 0 可用额度比值 0 年龄 0 逾期30-59天笔数 0 负债率 0 月收入 29221 信贷数量 0 逾期90天笔数 0 固定资产贷款量 0 逾期60-89天笔数 0 家属数量 3828 dtype: int64
家属人数列缺失数据比较少可以考虑直接删除,月收入缺失数据比较多,使用均值填充。
- 新的填充方式:df.fillna({col:xxx})
# 对'家属数量'带有空值的行删除 data = data.loc[data['家属数量'].notnull()] # 对'月收入'带有空值的行用均值进行填充 # 新的填充方式:df.fillna({col:xxx}) data.fillna({'月收入': data['月收入'].mean()},inplace=True) # 恢复行索引 data.index = range(data.shape[0]) # 再次查看是否有缺失值 data.isnull().sum() 好坏客户 0 可用额度比值 0 年龄 0 逾期30-59天笔数 0 负债率 0 月收入 0 信贷数量 0 逾期90天笔数 0 固定资产贷款量 0 逾期60-89天笔数 0 家属数量 0 dtype: int64
异常数据处理
- 但在银行数据中,我们希望排除的“异常值”不是一些超高或超低的数字,而是 一些不符合常理的数据:比如,收入不能为负数,但是一个超高水平的收入却是合理的,可以存在的。所以在银行 业中,我们往往就使用普通的描述性统计来观察数据的异常与否与数据的分布情况。注意,这种方法只能在特征量 有限的情况下进行,如果有几百个特征又无法成功降维或特征选择不管用
# 查看数据描述 data.describe().T
# 查看数据描述,通过列表指定所对应得比例,更容易发现问题,发现异常值如下 data.describe([0.1,0.25,0.5,0.75,0.9,0.99]).T

年龄的最小值居然有0,这不符合银行的业务需求,即便是儿童账户也要至少8岁,我们可以 查看一下年龄为0的人有多少
(data['年龄'] == 0).sum() # 有一个年龄为0得数据 直接删除
- 发现只有一个人年龄为0,可以判断这肯定是录入失误造成的,可以当成是缺失值来处理,直接删除掉这个样本
- 可以适当的恢复索引
data = data.loc[data['年龄'] != 0]
- 另外,有三个指标看起来很奇怪:逾期30-59天笔数,逾期60-89天笔数,逾期90天笔数(这三个特征指的是两年内逾期次数),这三个特征最大值为98,看起来非常奇怪。一个人在过去两年内逾期35~59天98次,一年6个60天,两年内逾期98次这是怎么算出来的?将其删除
- 可以适当的恢复索引
# 将大于90天得统一去掉 data = data.loc[data['逾期30-59天笔数']<90] data = data.loc[data['逾期60-89天笔数']<90] data = data.loc[data['逾期90天笔数']<90] # 恢复索引 data.index = range(data.shape[0]) # 查看标签分布情况 data['好坏客户'].value_counts() 0 135648 1 9706 Name: 好坏客户, dtype: int64 # 分布有点不均衡,但可以使用逻辑回归模型参数处理 data['好坏客户'].value_counts() / data['好坏客户'].value_counts().sum() 0 0.933225 1 0.066775 Name: 好坏客户, dtype: float64 data.shape # (145354, 11)
特征选择
- 单变量分析
- IV&WOE编码
单变量分析
- 是分析每一个自变量和因变量之间的联系,此处以年龄和好坏客户为例进行分析。
这里仅对年龄进行单变量分析
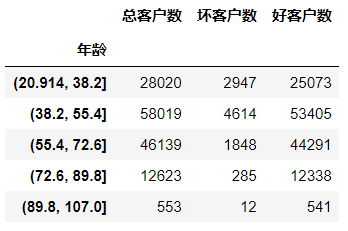
#对年龄进行分箱操作,分成5组 age_cut = pd.cut(data['年龄'],bins=5) age_cut.value_counts() (38.2, 55.4] 58019 (55.4, 72.6] 46139 (20.914, 38.2] 28020 (72.6, 89.8] 12623 (89.8, 107.0] 553 Name: 年龄, dtype: int64 # 基于分组求出每个不同年龄段对应用户的数量 # 注意:对Series进行分组计数,使用另一个Series对其分组然后计数 (注意,以前没用过) sum_user_age = data['好坏客户'].groupby(by=age_cut).count() 年龄 (20.914, 38.2] 28020 (38.2, 55.4] 58019 (55.4, 72.6] 46139 (72.6, 89.8] 12623 (89.8, 107.0] 553 Name: 好坏客户, dtype: int64 # 对各组的坏客户数 # 因为0是好用户,1是坏用户,求和0不会计入 bad_user_sum = data['好坏客户'].groupby(by=age_cut).sum() 年龄 (20.914, 38.2] 2947 (38.2, 55.4] 4614 (55.4, 72.6] 1848 (72.6, 89.8] 285 (89.8, 107.0] 12 Name: 好坏客户, dtype: int64 # 级联 age_cut_group = pd.concat((sum_uer_age,bad_user_sum),axis=1) # 级联后发现列索引有问题,修改列索引 age_cut_group.columns = ['总客户数','坏客户数']
# 添加一列好客户数量 age_cut_group['好客户数'] = age_cut_group['总客户数'] - age_cut_group['坏客户数']
# 在添加一列坏客户占比 age_cut_group['坏客户占比'] = age_cut_group['坏客户数'] / age_cut_group['总客户数']
# 使用柱状图表示不同年龄段好坏客户的数量 # 指定后可以显示中文 from pylab import mpl mpl.rcParams['font.sans-serif'] = ['FangSong'] # 指定默认字体 mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题 ax1 = age_cut_group[['好客户数','坏客户数']].plot.bar(figsize=(10,5)) ax1.set_xticklabels(age_cut_group.index,rotation=15) ax1.set_ylabel('客户数量')
# 绘制线型图 ax11 = age_cut_group["坏客户占比"].plot(figsize=(10,5)) ax11.set_xticklabels([0,20,29,38,47,55,64,72,81,89,98,107]) ax11.set_ylabel("坏客户率") ax11.set_title("坏客户率随年龄的变化趋势图")

- 可以看出随着年龄的增长,坏客户率在降低,其中38~55之间变化幅度最大,说明年龄特征对好坏客户的判定影响还是比较大的
- 如果图是一条基本平行于x轴的直线,说明特征对分类结果影响不大,可以在特征选择时不选择它
使用IV值进行特征选择
分箱操作
# 分箱操作 cut1=pd.qcut(data["可用额度比值"],4) cut2=pd.cut(data["年龄"],8) bins3=[-1,0,1,3,5,13] cut3=pd.cut(data["逾期30-59天笔数"],bins3) cut4=pd.qcut(data["负债率"],3) cut5=pd.qcut(data["月收入"],4) cut6=pd.cut(data["信贷数量"],4) bins7=[-1, 0, 1, 3,5, 20] cut7=pd.cut(data["逾期90天笔数"],bins7) bins8=[-1, 0,1,2, 3, 33] cut8=pd.cut(data["固定资产贷款量"],bins8) bins9=[-1, 0, 1, 3, 12] cut9=pd.cut(data["逾期60-89天笔数"],bins9) bins10=[-1, 0, 1, 2, 3, 5, 21] cut10=pd.cut(data["家属数量"],bins10)
封装计算WOE的函数
pd.crosstab(cut1,data['好坏客户']) # 封装计算WOE的函数 def get_woe_data(cut): gb = data['好坏客户'].value_counts() # 整个样本中好坏客户的样本数量 gi = pd.crosstab(cut,data['好坏客户']) # 每组中正反例样本数量 gbi = (gi[1] / gi[0])/(gb[1] / gb[0]) woe = np.log(gbi) # ln(gbi) return woe cut1.value_counts() (-50.708, 12677.0] 145344 (12677.0, 25354.0] 8 (38031.0, 50708.0] 1 (25354.0, 38031.0] 1 Name: 可用额度比值, dtype: int64 # 测试get_woe_data函数效果 # 如果返回-inf则将cut换为qcut,因为在-inf对应的区间计算出来的woe极小,无意义 get_woe_data(cut1) # 这里出现了 -inf # 某个箱子中的数量太少经过ln(gbi)后的值特别小就会使-inf # 如果出现-inf可以使用qcut进行分箱 可用额度比值 (-50.708, 12677.0] 0.000074 (12677.0, 25354.0] -inf (25354.0, 38031.0] -inf (38031.0, 50708.0] -inf dtype: float64 get_woe_data(cut1) # 改为qcut后 可用额度比值 (0.558, 50708.0] -1.322345 (0.158, 0.558] -1.225098 (-0.001, 0.0311] -0.294389 (0.0311, 0.158] 1.101834 dtype: float64
封装计算IV的函数
# 封装计算IV的函数 def get_iv_data(cut): gb = data['好坏客户'].value_counts() # 整个样本中好坏客户的样本数量 gi = pd.crosstab(cut,data['好坏客户']) # 每组中正反例样本数量 gbi = (gi[1] / gi[0])/(gb[1] / gb[0]) woe = np.log(gbi) # ln(gbi) # iv = (py-pn) * woe中的py为一组中正例样本和整个样本集中正例样本的比例 iv = ((gi[1]/gb[1])-(gi[0]/gb[0])) * woe return iv get_iv_data(cut1) 可用额度比值 (0.558, 50708.0] 0.254973 (0.158, 0.558] 0.227016 (-0.001, 0.0311] 0.019093 (0.0311, 0.158] 0.488091 dtype: float64
绘制bins分箱学习曲线寻找最优bins分箱数
- 以年龄特征为例,分箱个数范围5-15为例测试
# 绘制bins学习曲线寻找最佳bins分箱数 ivs = [] bins = [] for i in range(5,15): cut = pd.cut(data['年龄'], bins=i) iv_value = get_iv_data(cut).sum() # 求当前特的正iv值 ivs.append(iv_value) bins.append(i) plt.plot(bins,ivs) # 绘制bins学习曲线 # 由图可以看出最佳的bins为13
求出每一列特征的IV值
# 记住这里需要使用sum求的是每个特征的iv值 cut1_iv = get_iv_data(cut1).sum() cut2_iv = get_iv_data(cut2).sum() cut3_iv = get_iv_data(cut3).sum() cut4_iv = get_iv_data(cut4).sum() cut5_iv = get_iv_data(cut5).sum() cut6_iv = get_iv_data(cut6).sum() cut7_iv = get_iv_data(cut7).sum() cut8_iv = get_iv_data(cut8).sum() cut9_iv = get_iv_data(cut9).sum() cut10_iv = get_iv_data(cut10).sum()
特征变量与IV值分布图
from pylab import mpl mpl.rcParams['font.sans-serif'] = ['FangSong'] # 指定默认字体 mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题 IV=pd.DataFrame([cut1_iv,cut2_iv,cut3_iv,cut4_iv,cut5_iv,cut6_iv,cut7_iv,cut8_iv,cut9_iv,cut10_iv],index=['可用额度比值','年龄','逾期30-59天笔数','负债率','月收入','信贷数量','逾期90天笔数','固定资产贷款量','逾期60-89天笔数','家属数量'],columns=['IV']) iv=IV.plot.bar(color='b',alpha=0.3,rot=30,figsize=(10,5),fontsize=(10)) iv.set_title('特征变量与IV值分布图',fontsize=(15)) iv.set_xlabel('特征变量',fontsize=(15)) iv.set_ylabel('IV',fontsize=(15))

IV值替换特征元素
#使用IV值替换原始特征元素 def map_op(cut): #获取每一列特征分箱后的映射关系表 dic = get_iv_data(cut).to_dict() #进行映射操作,将原始数据替换成特征的IV值 return pd.Series(cut.tolist()).map(dic) cuts = [cut1,cut2,cut3,cut4,cut5,cut6,cut7,cut8,cut9,cut10] cuts_iv_list = [] for cut in cuts: cuts_iv_list.append(map_op(cut)) data_arr = np.array(cuts_iv_list) new_df = pd.DataFrame(data=data_arr).T new_df.columns = ['可用额度比值','年龄','逾期30-59天笔数','负债率','月收入','信贷数量','逾期90天笔数','固定资产贷款量','逾期60-89天笔数','家属数量'] new_df['好坏客户'] = data['好坏客户'] new_df.head()
对new_df中可能存在的空值进行过滤(分箱时可能存在有些值没有地方可分,这样映射得时候就会用空补上)
如果有空值建模时会报错
- 空值存在的原因:分箱设置的每个箱子的范围可能会包含不了所有的特征元素
- 例如:查看第三个特征本身的数值范围和分箱后的每组范围:
- data.iloc[3].value_counts()
- bins3=[-1,0,1,3,5,13]
# 对空值进行删除 new_df.dropna(axis=0,inplace=True) # 查看是否有空值 new_df.isnull().sum() 可用额度比值 0 年龄 0 逾期30-59天笔数 0 负债率 0 月收入 0 信贷数量 0 逾期90天笔数 0 固定资产贷款量 0 逾期60-89天笔数 0 家属数量 0 好坏客户 0 dtype: int64
建立逻辑回归模型
from sklearn.model_selection import train_test_split from sklearn.metrics import roc_auc_score,f1_score from sklearn.linear_model import LogisticRegression # 提取样本数据 feature = new_df.iloc[:,:-1] target = new_df.iloc[:,-1] # 对数据进行切分 x_train,x_test,y_train,y_test = train_test_split(feature,target,test_size=0.1,random_state=0) # 训练模型 # 这可以在LogisticRegression中平衡样本不均衡的参数class_weight=balanced l = LogisticRegression().fit(x_train,y_train) # 查看模型f1_score 这里二分类需要指定参数average='micro' y_pred = l.predict(x_test) f1_score(y_test,y_pred,average='micro') # 0.9336130985140341 # 获取某一样本的分类概率 y_score = l.predict_proba(x_test)[:,1] array([0.08220902, 0.04613142, 0.02187967, ..., 0.02180471, 0.03986075, 0.01944439]) # AUC 二分类用的模型评分 roc_auc_score(y_test,y_score) # y_score只能取出某一列的分类概率 0.7681435541928233 # 可以将分到0的概率作为征信评分 l.predict_proba(x_test)[:,0] * 100 array([91.77909832, 95.38685776, 97.81203296, ..., 97.81952926, 96.01392514, 98.05556134])