线性图:plt.plot()
- 绘制单条线形图
- 绘制多条线形图
- 设置坐标系的比例plt.figure(figsize=(a,b))
- 设置图例legend()
- 设置轴的标识
- 图例保存
- fig = plt.figure()
- plt.plot(x,y)
- figure.savefig()
- 曲线的样式和风格(自己研究)
# x与y满足什么线性关系,就能绘制出什么样的图片
x = np.array([1,2,3,4,5])
y = x + 2
plt.plot(x,y)
# 抛物线
x = x
y = x**2
plt.plot(x,y)
# 在一个坐标系中绘制多条曲线
plt.plot(x,y)
plt.plot(x-2,y+3)
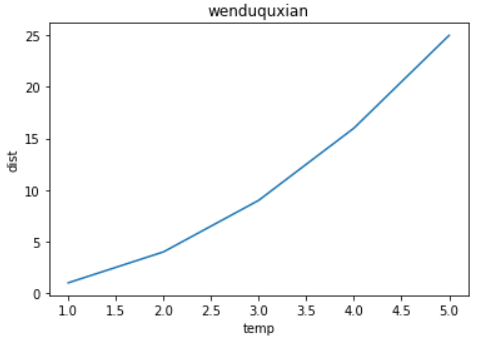
# 设置轴表示的含义
plt.plot(x,y)
plt.xlabel('temp') # x轴
plt.ylabel('dist') # y轴
plt.title('wenduquxian') # 标题
#设置图例
plt.plot(x,y,label='line_a')
plt.plot(x-2,y+3, label='line_b')
plt.legend()
# 等比例的放大或者缩小坐标系(坐标的刻度是不会发生改变)
plt.figure(figsize=(9,6)) # 这段代码一定要写在绘图操作之前
plt.plot(x,y,label='line_a')
plt.plot(x-2,y+3, label='line_b')
plt.legend()
# 保存图像必须按照下边这个步骤
# 1.实例化对象
fig = plt.figure()
# 2.绘图
plt.plot(x,y,label='aaa')
plt.plot(x-2,y+3,label='bbb')
plt.legend()
# 3.保存图片
fig.savefig('./123.png')
柱状图:plt.bar()
- 参数:第一个参数是索引。第二个参数是数据值。第三个参数是条形的宽度
x = [1,2,3,4,5] # 横坐标
y = [3,8,5,7,6] # 柱高
plt.bar(x,y)
x = [1,2,3,4,5]
y = [3,8,5,7,6]
plt.barh(x,y) # barh是让它躺下啦
直方图:plt.hist()
- 是一个特殊的柱状图,又叫做密度图
- plt.hist()的参数
- bins
可以是一个bin数量的整数值,也可以是表示bin的一个序列。默认值为10
- normed
如果值为True,直方图的值将进行归一化处理,形成概率密度,默认值为False
- color
指定直方图的颜色。可以是单一颜色值或颜色的序列。如果指定了多个数据集合,例如DataFrame对象,颜色序列将会设置为相同的顺序。如果未指定,将会使用一个默认的线条颜色
- orientation
通过设置orientation为horizontal创建水平直方图。默认值为vertical
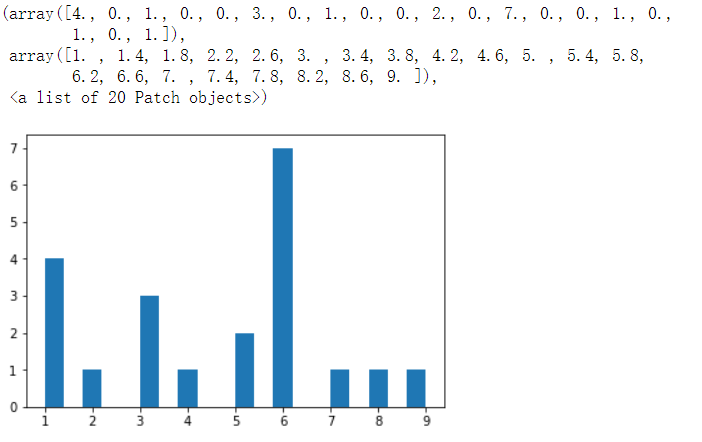
x = [1,1,1,1,2,3,3,3,4,5,5,6,6,6,6,6,6,6,7,8,9]
plt.hist(x, bins=20) # bins表示柱子的个数
# 图中没显示20个柱子是因为有些柱高为0
# 一共20个数
(array([4., 0., 1., 0., 0., 3., 0., 1., 0., 0., 2., 0., 7., 0., 0., 1., 0.,
1., 0., 1.]),
# 一共21个数,俩俩一区间,上边array对应x中元素在这个区间出现的次数
array([1. , 1.4, 1.8, 2.2, 2.6, 3. , 3.4, 3.8, 4.2, 4.6, 5. , 5.4, 5.8,
6.2, 6.6, 7. , 7.4, 7.8, 8.2, 8.6, 9. ]),
<a list of 20 Patch objects>)
饼图:plt.pie()
- pie(),饼图也只有一个参数x
- 饼图适合展示各部分占总体的比例,条形图适合比较各部分的大小
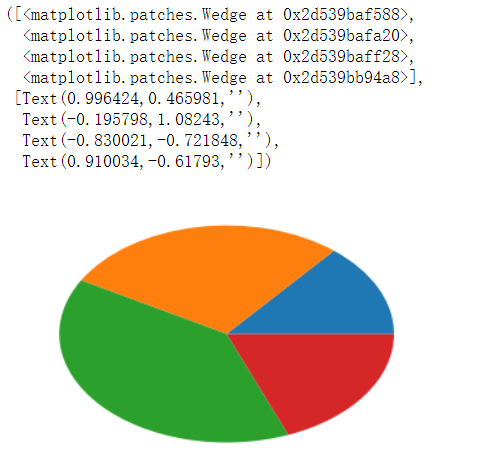
arr=[11,22,31,15] # 每个数所占整体和的比例
plt.pie(arr)
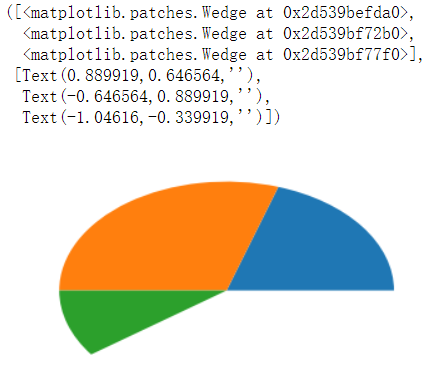
arr=[0.2,0.3,0.1] # 小数对应的是该数乘以100%的比例
plt.pie(arr)
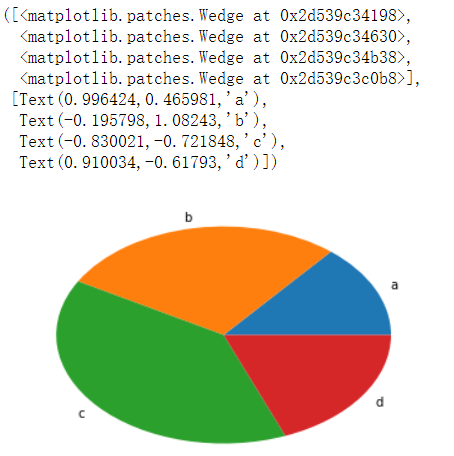
# labels 对每个组成部分起一个标识
arr=[11,22,31,15]
plt.pie(arr,labels=['a','b','c','d'])
# labeldistance 给标识设置它离圆心的距离
arr=[11,22,31,15]
plt.pie(arr,labels=['a','b','c','d'],labeldistance=0.3)
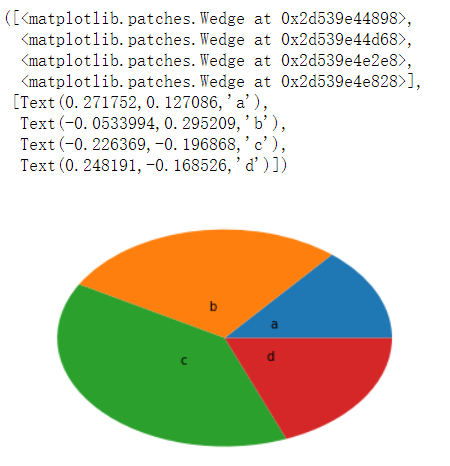
# autopct 每个组成部分所占百分比,保留3小数
arr=[11,22,31,15]
plt.pie(arr,labels=['a','b','c','d'],labeldistance=0.3,autopct='%.3f%%')
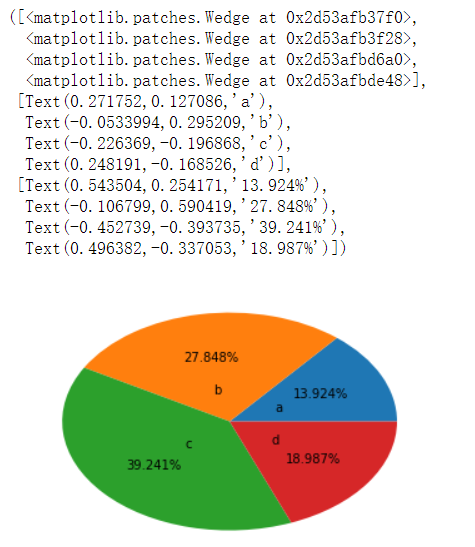
# explode 指定每个部分离圆心的距离
arr=[11,22,31,15]
plt.pie(arr,labels=['a','b','c','d'],labeldistance=0.3,shadow=True,explode=[0.2,0.3,0.2,0.4])
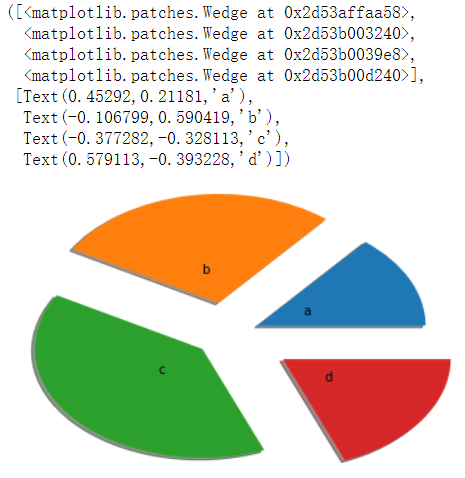
散点图:plt.scatter()
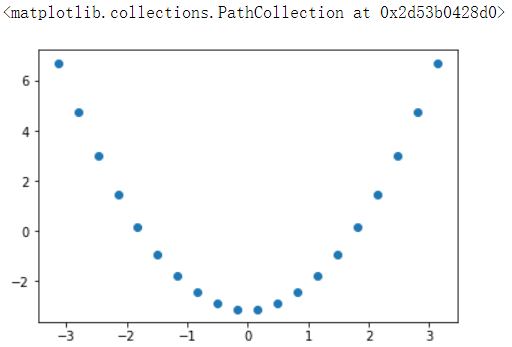
x = np.linspace(-np.pi,np.pi, num=20)
y = x**2 - 3.14
# 这样散点图就满足一个线性关系
plt.scatter(x,y)
x = np.linspace(-np.pi,np.pi,num=20)
y = np.random.randint(0,20,size=(20,))
# 这样散点图就不存在线性关系
plt.scatter(x,y)
Seaborn




















