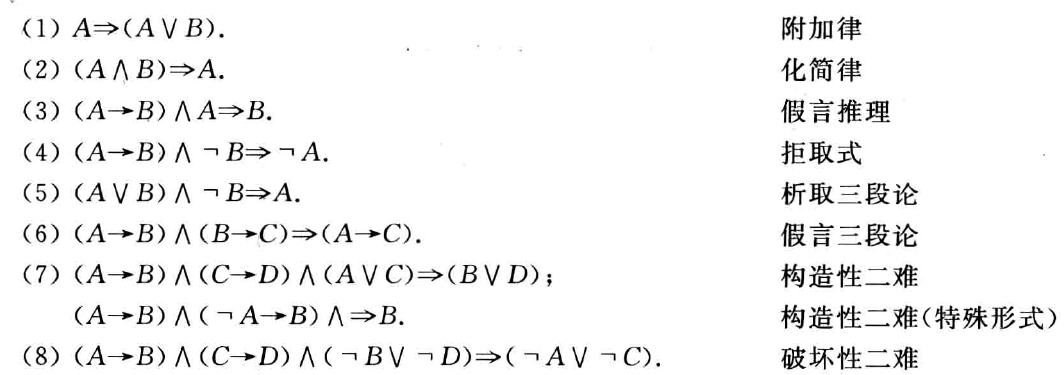离散数学知识点整理（一）

离散数学

数学语言与证明方法

集合

  • 幂集

  • 运算

    • 交集
    • 并集
    • 相对补集
    • 绝对补集
    • 对称差集

  • 运算律

    • 交换律
    • 结合律
    • 分配律
    • 德摩根律

  • 恒等式

证明方法

  • 直接证明
  • 归谬法
  • 分情况证明
  • 构造性证明
  • 数学归纳法

命题逻辑

命题

  • 简单命题p,q,r

  • 复合命题

    • 基本复合命题

      • 五种

    • 复杂复合命题

  • 真值

    • 真命题
    • 假命题

  • 命题符号化

联结词

  • 否定联结词\(\lnot\)

    • 否定式

  • 合取联结词\(\land\)

    • 合取式

  • 析取联结词\(\lor\)

    • 析取式

      • 相容或\(p\lor q\)
      • 排斥或\((\lnot p\land q)\lor(p\land \lnot q)\)

  • 蕴含联结词

    • 蕴含式

      • p->q

        • 真值

          • p真q假，p->q为真
          • 其他全为真

      • 前件p

      • 后件q

  • 等价联结词

    • 等价式

      • p<->q

        • 真值

          • p,q真值相同，p<->q为真
          • 不同为假

      • ‘当且仅当’

公式

  • 命题

    • 常项

      • p,q,r为定值

    • 变项

      • p,q,r为变量

  • 合式公式/命题公式

    • A，B，C，D

      • 永真式

        • 重言式

      • 永假式

        • 矛盾式

      • 可满足式

  • 赋值/解释

    • 成真赋值
    • 成假赋值

  • 等值演算

    • A<->B，则A<=>B

      • 等价式为重言式

    • 常用等值公式

      • 蕴含等值式 \(A\rightarrow B\Leftrightarrow\lnot A\lor B\)
      • 德摩根律 \(\lnot (A\lor B)\Leftrightarrow \lnot A \land \lnot B\)

联结词集

  • 优先顺序

  • 扩展

    • 与非联结词

      • \(p\uparrow q\Leftrightarrow \lnot(p\land q)\)

    • 或非联结词

      • \(p\downarrow q\Leftrightarrow \lnot(p\lor q)\)

  • 联结词完备集

    • (1)\(S=\{\lnot,\land,\lor\}\)
    • (2)\(S=\{\uparrow\}\)
    • (3)\(S=\{\downarrow\}\)

范式

  • 分类

    • 析取范式

      • 主析取范式

        • 极大项

    • 合取范式

      • 主合取范式

        • 极小项

  • 计算

推理

  • 概念

    • 蕴含式为重言式

      • \(\Rightarrow\)

  • 形式结构

    • \((A_1\land A_2 \land ...\land A_k)\Rightarrow B\)

      • 前提
      • 结论

  • 证明

    • 推理规则

      • 前提引入

      • 结论引入

      • 置换规则

        • 等值置换

          • \(A\Leftrightarrow B:A\Rightarrow B;B\Rightarrow A\)

      • 推理定律

    • 特殊证明方法

      • 附加前提证明法

        • \((A_1\land A_2 \land ...\land A_k)\Rightarrow A\rightarrow B\)
        • \((A_1\land A_2 \land ...\land A_k \land A)\Rightarrow B\)

      • 归结证明法

        • 归结规则

          • \((L\lor C_1)\land (\lnot L\lor C_2)\Rightarrow C_1\lor C_2\)

        • 基本思想

          • 归谬法

        • 证明步骤

          • 结论的否定引入前提
          • 把所有前提化成合取范式，并将简单析取式作为单个前提
          • 归结规则进行推理
          • 推出0则推理正确

一阶逻辑

表达个体与总体之间的内在联系与数量关系

概念

  • 个体词

    • 个体常项

      • a,b,c....

    • 个体变项

      • 个体域
      • x,y,z....

  • 谓词

    • 谓词常项

      • 表示具体性质或关系
      • 子主题 2

    • 谓词变项

      • 表示抽象性质或关系
      • F，G....

    • 0元谓词

      • 不带个体变项的谓词
      • 当谓词为谓词常项时为命题

  • 量词

    • 全称量词
    • 存在量词

符号化

  • 不同个体域形式可能不同
  • 引入特性谓词

公式

  • 分类

    • 原子公式

    • 合式公式/谓词公式

    • 闭式

      • A中不含自由出现的个体变项

  • 概念

    • x:指导变元
    • A:辖域
    • x在A中约束出现
    • A中出现的除x所有其他个体变项都为自由出现

  • 解释/赋值

    • 定义

    • 封闭的公式在任何解释下都变成命题

    • 分类

      • 永真式/逻辑有效式

        • A在任何解释和任何赋值下均为真

      • 永假式/矛盾式

        • A在任何解释和任何赋值下均为假

      • 可满足式

        • 至少存在一个解释和一个赋值使A为真

    • 代换实例

      • 重言式的代换实例都是重言式
      • 矛盾式的代换实例都是矛盾式

  • 等值演算

    • 命题逻辑的代换实例

    • 等值式

      • 消去量词等值式
      • 量词否定等值式
      • 量词辖域收缩与扩张等值式
      • 量词分配等值式

    • 规则

      • 置换规则
      • 换名规则

  • 前束范式

    • 存在但不唯一
    • 利用等值演算求前束范式

posted @ 2020-07-08 10:15  wgjmcal  阅读(1719)  评论(0)  编辑  收藏  举报