IDEA中通义灵码的使用技巧
大家好,我是 V 哥。在日常写代码的过程中,通过 AI 工具辅助开发已是当下程序员惯用的方式,V 哥在使用了众多的 AI 工具后,多数情况下,选择通义灵码来辅助开发,尤其是解释代码和生成单元测试功能甚是好用,听 V 哥来详细聊聊。
通义灵码安装
打开你的 IDEA 开发工具,在菜单栏中选择Settings,打开设置窗口,在左侧栏中选择 Plugins,在 Marketplace 的搜索栏中输入“通义灵码”,搜索结果的第一个就是通义灵码 AI 插件了,点击 Install 安装插件后,重启 IDE 即可安装成功。
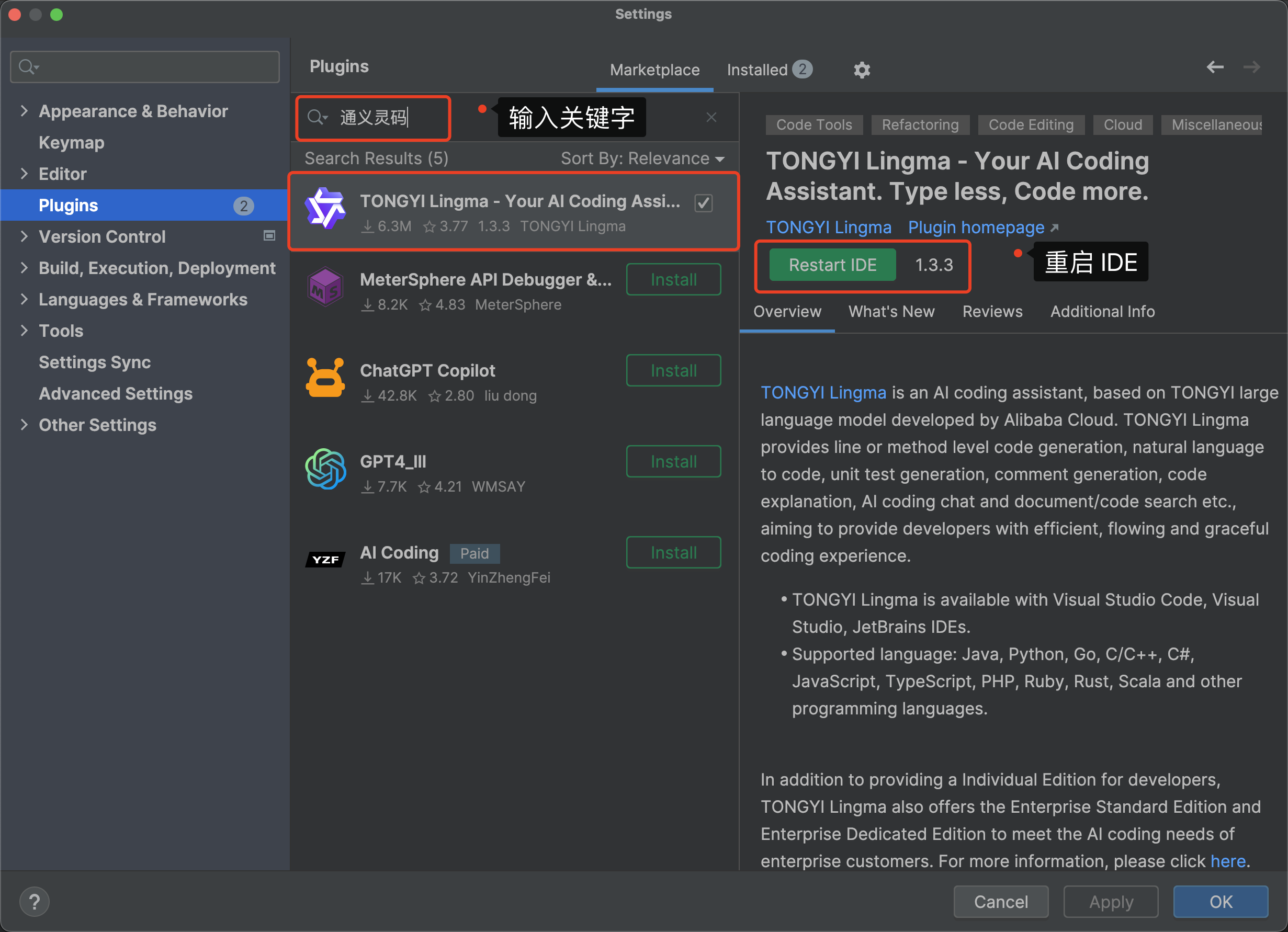
重启IDEA后,在右侧会出现通义灵码选项,此时,就可以使用通义灵码来辅助编程啦。
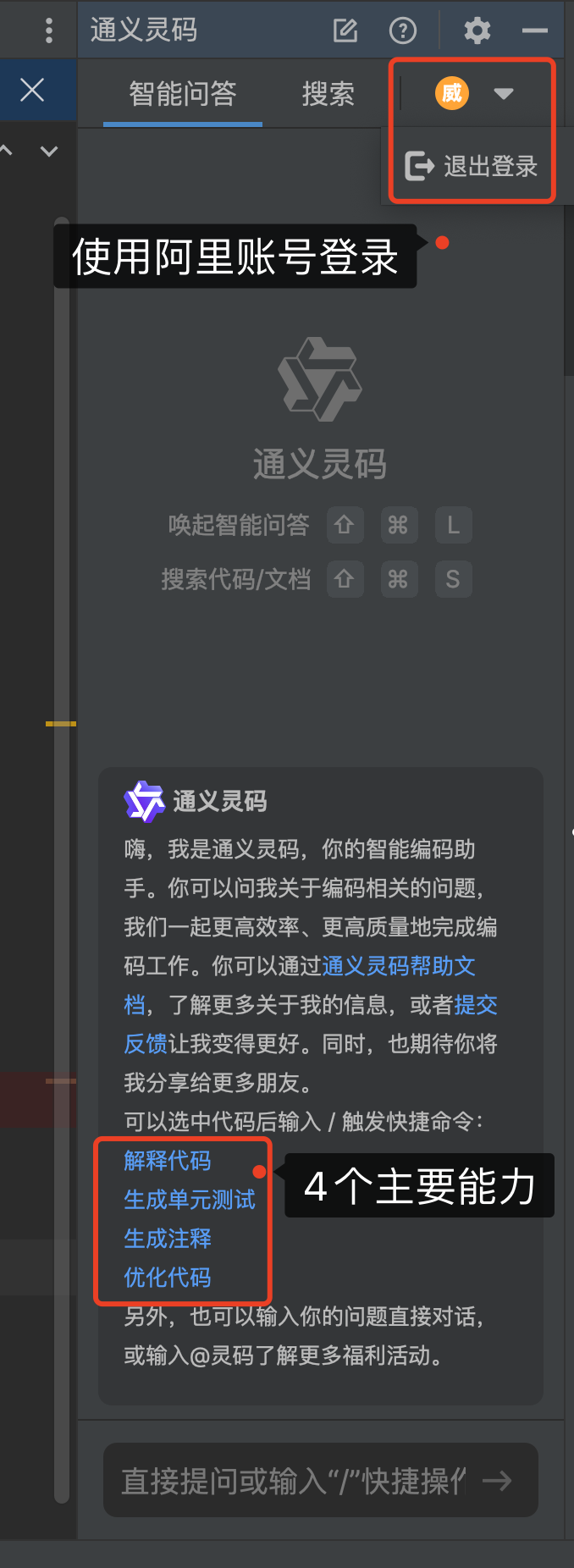
使用前,请先使用阿里账号进行登录,V 哥的账号是威哥爱编程。
通过通义灵码 AI 工具解释代码
V 哥写了一个 DFS 算法,代码如下:
/**
* description:
* author: V哥
* wx:finally-weige
*/
public class DFSMazeSolver {
private static final int[] DX = {-1, 1, 0, 0}; // 行移动方向:上,下
private static final int[] DY = {0, 0, -1, 1}; // 列移动方向:左,右
public boolean dfs(int[][] maze, int x, int y, boolean[][] visited) {
int rows = maze.length;
int cols = maze[0].length;
// 边界条件与目标判断
if (x < 0 || y < 0 || x >= rows || y >= cols || maze[x][y] == 0 || visited[x][y]) {
return false;
}
// 到达终点
if (x == rows - 1 && y == cols - 1) {
return true;
}
// 标记当前位置已访问
visited[x][y] = true;
// 递归地探索四个方向
for (int i = 0; i < 4; i++) {
int newX = x + DX[i];
int newY = y + DY[i];
if (dfs(maze, newX, newY, visited)) {
return true;
}
}
// 回溯
visited[x][y] = false;
return false;
}
public boolean canSolveMaze(int[][] maze) {
int rows = maze.length;
int cols = maze[0].length;
boolean[][] visited = new boolean[rows][cols];
return dfs(maze, 0, 0, visited);
}
public static void main(String[] args) {
int[][] maze = {
{1, 0, 0, 0},
{1, 1, 0, 1},
{0, 1, 0, 0},
{1, 1, 1, 1}
};
DFSMazeSolver solver = new DFSMazeSolver();
if (solver.canSolveMaze(maze)) {
System.out.println("路径可达");
} else {
System.out.println("无可行路径");
}
}
}
从代码上看,我已经加了少量代码注释,但对于小白或者初学者来说,想要完全理解代码的含义还是有些困难,下面我们来看看通义灵码的解释代码功能如何。
我们在代码中可以看到有通义灵码的图标标识,下拉打开后,即可以非常方便的使用助手功能了。
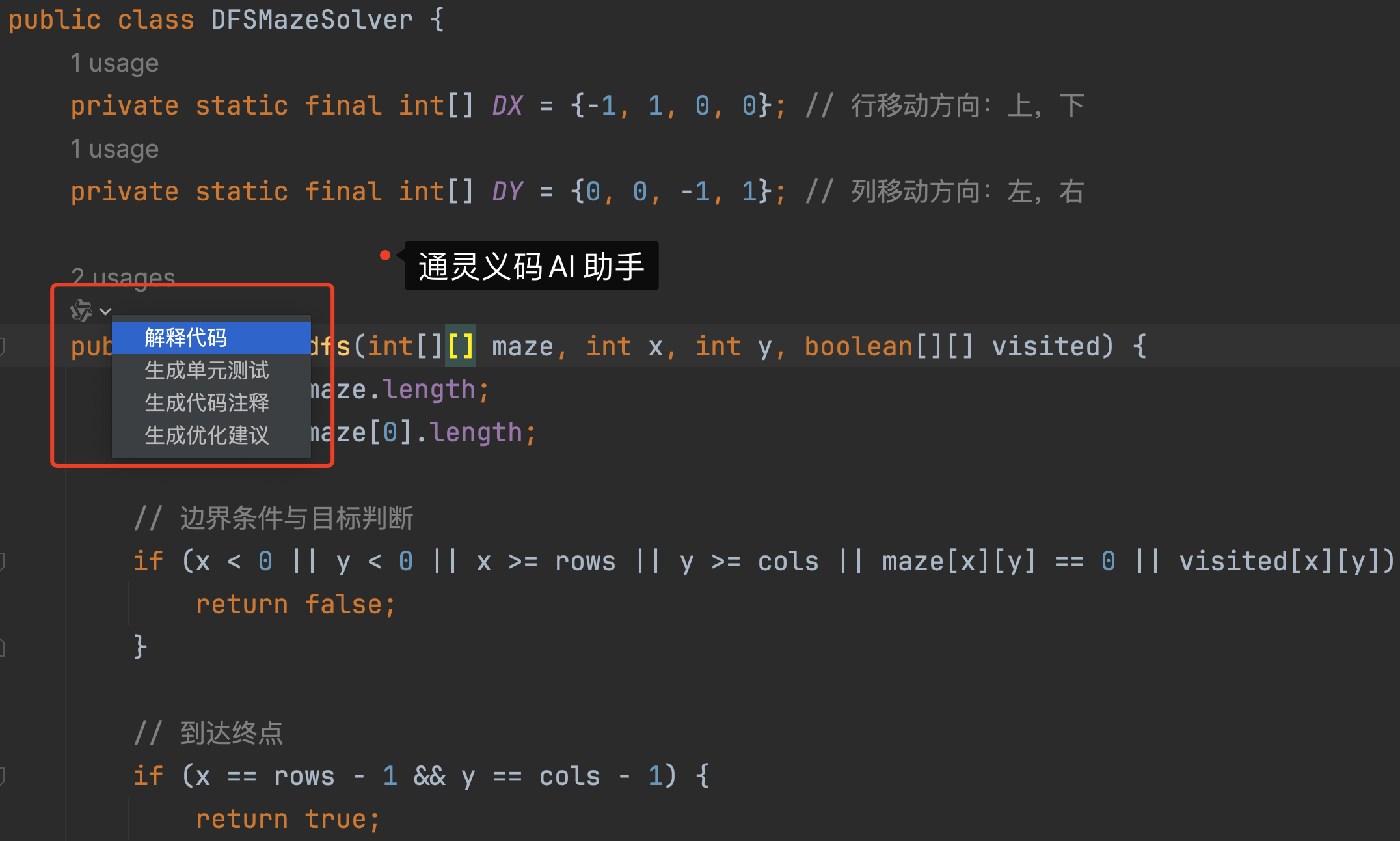
我们选择解释代码功能,通义灵码就是会以此方法 dfs 为目标,解释此方法的代码含义,我们来试试。
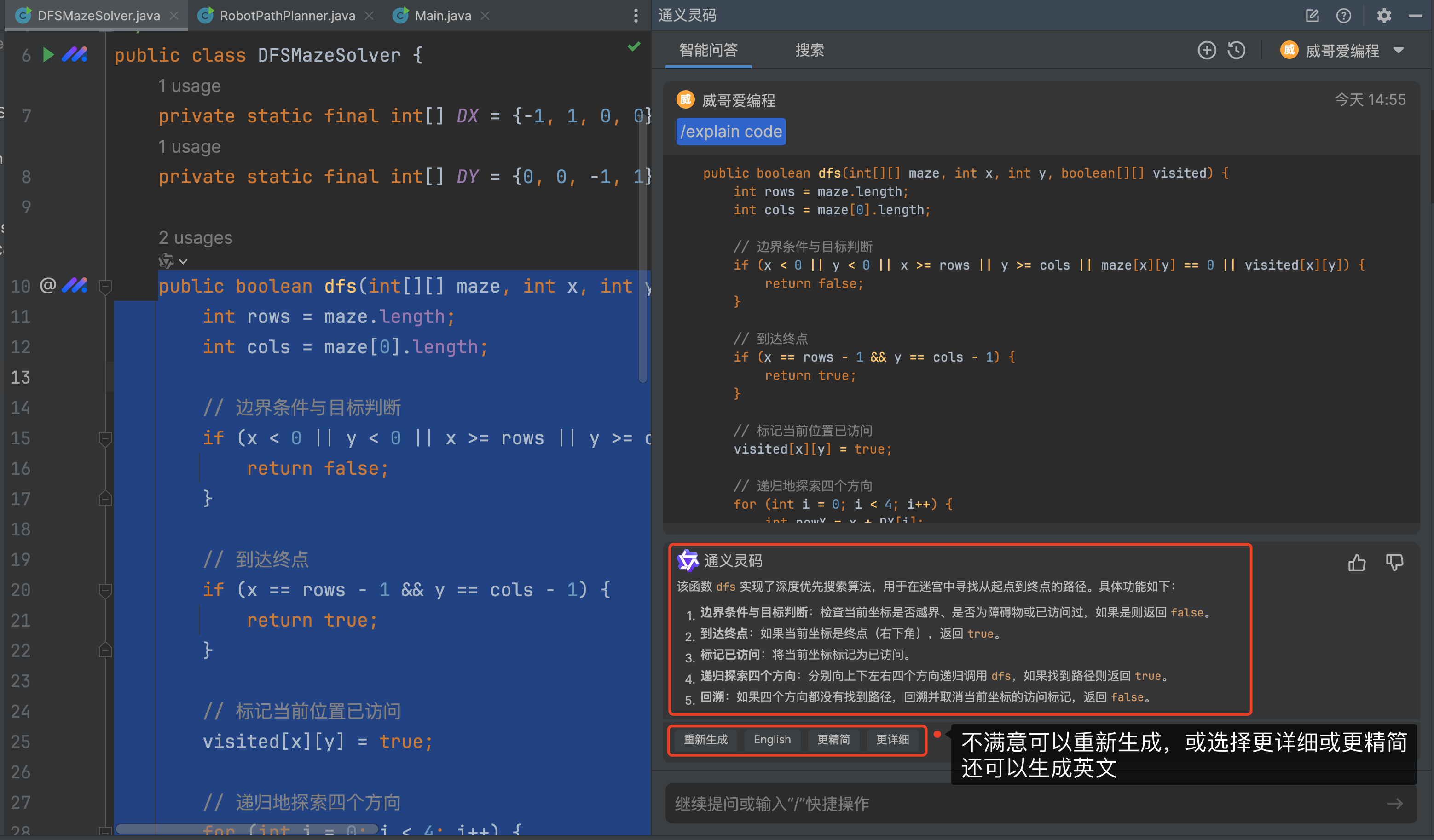
我们可以看到,在右侧通义灵码的功能区里会把目标方法的代码选中,下方是 dfs 方法的具体解释,从解释来看,基本达到了代码的含义理解,如果你不满意,还可以重新生成,通常 V 哥会使用更详细的解释功能,我们点击更详细来看看。
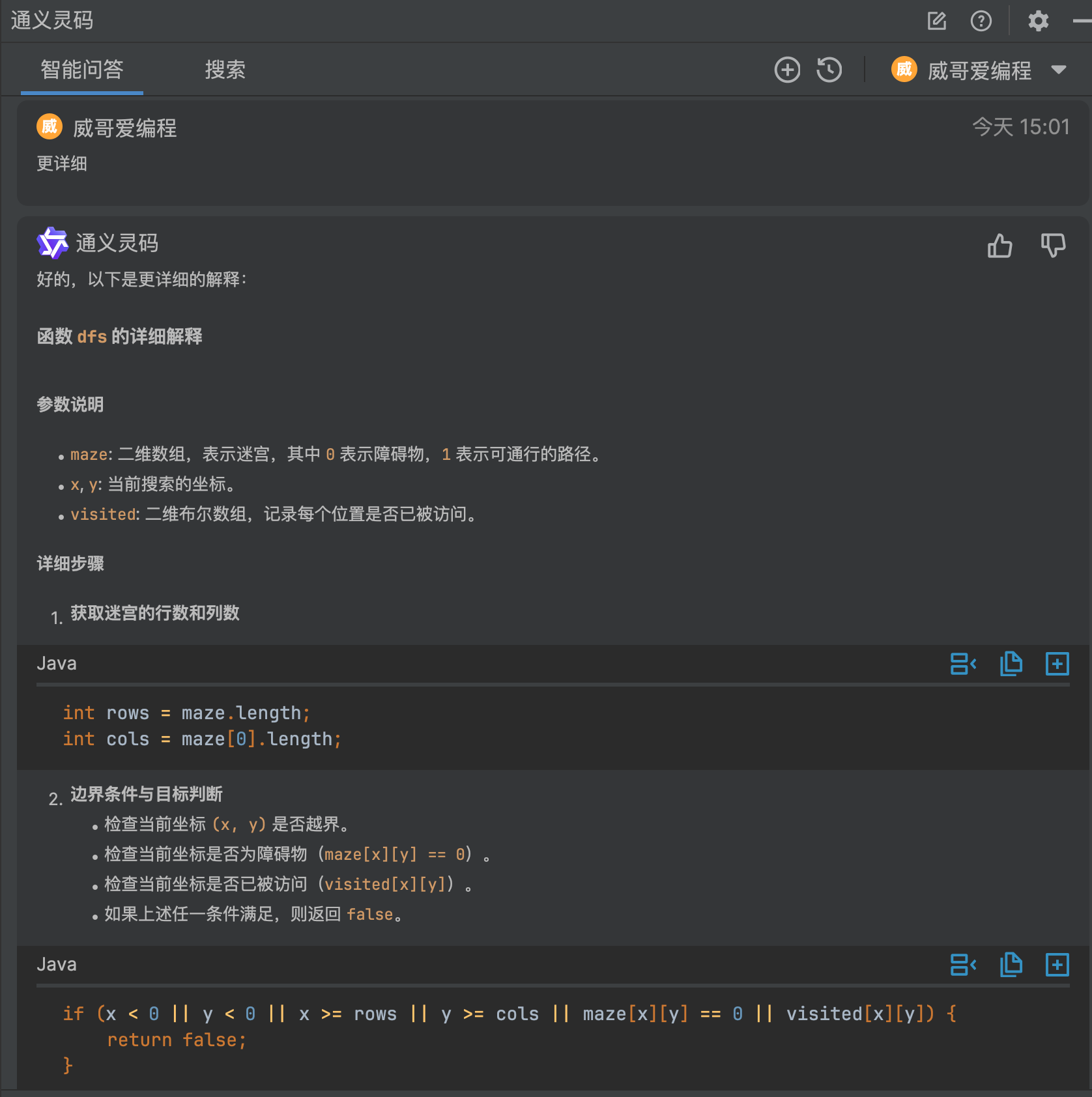
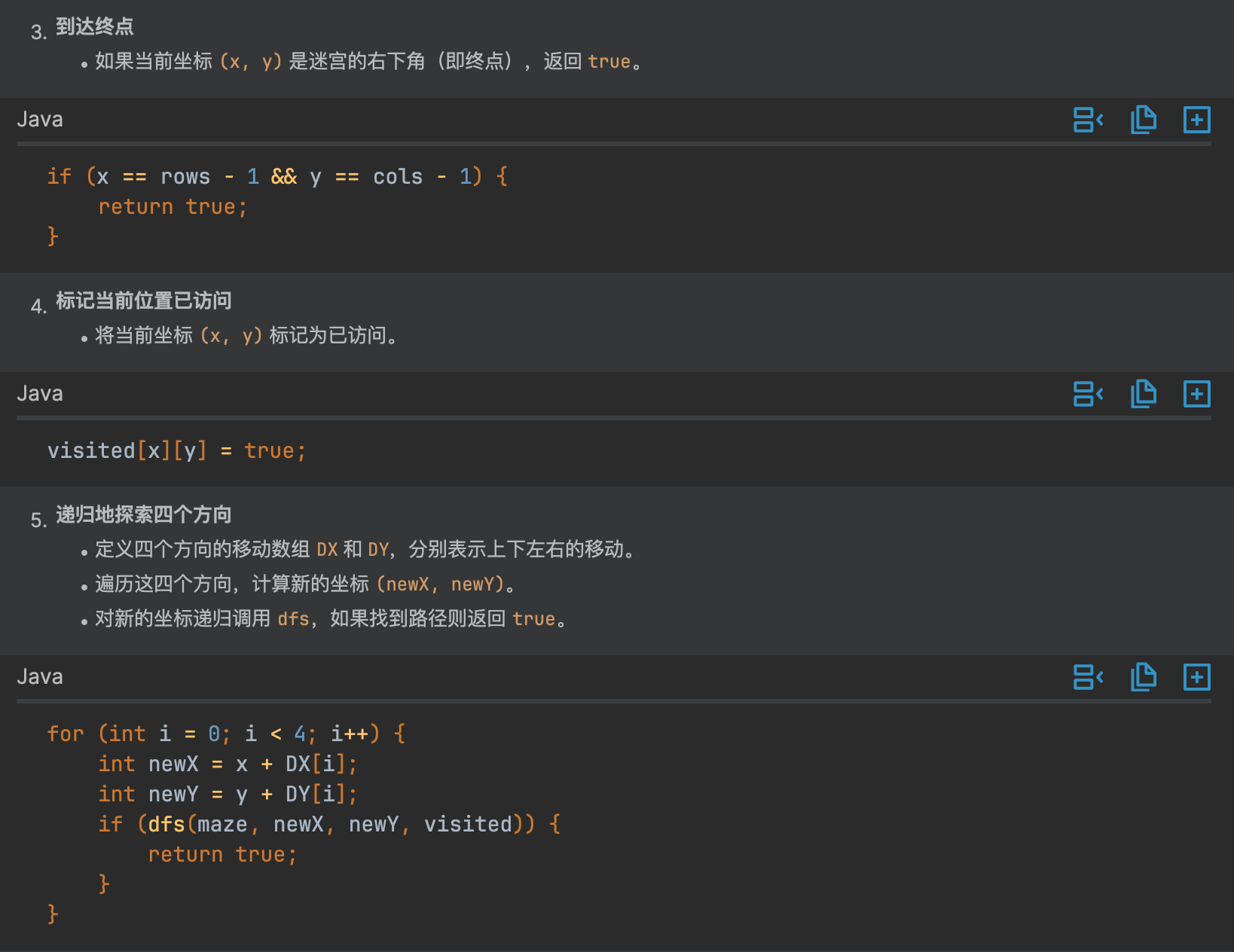
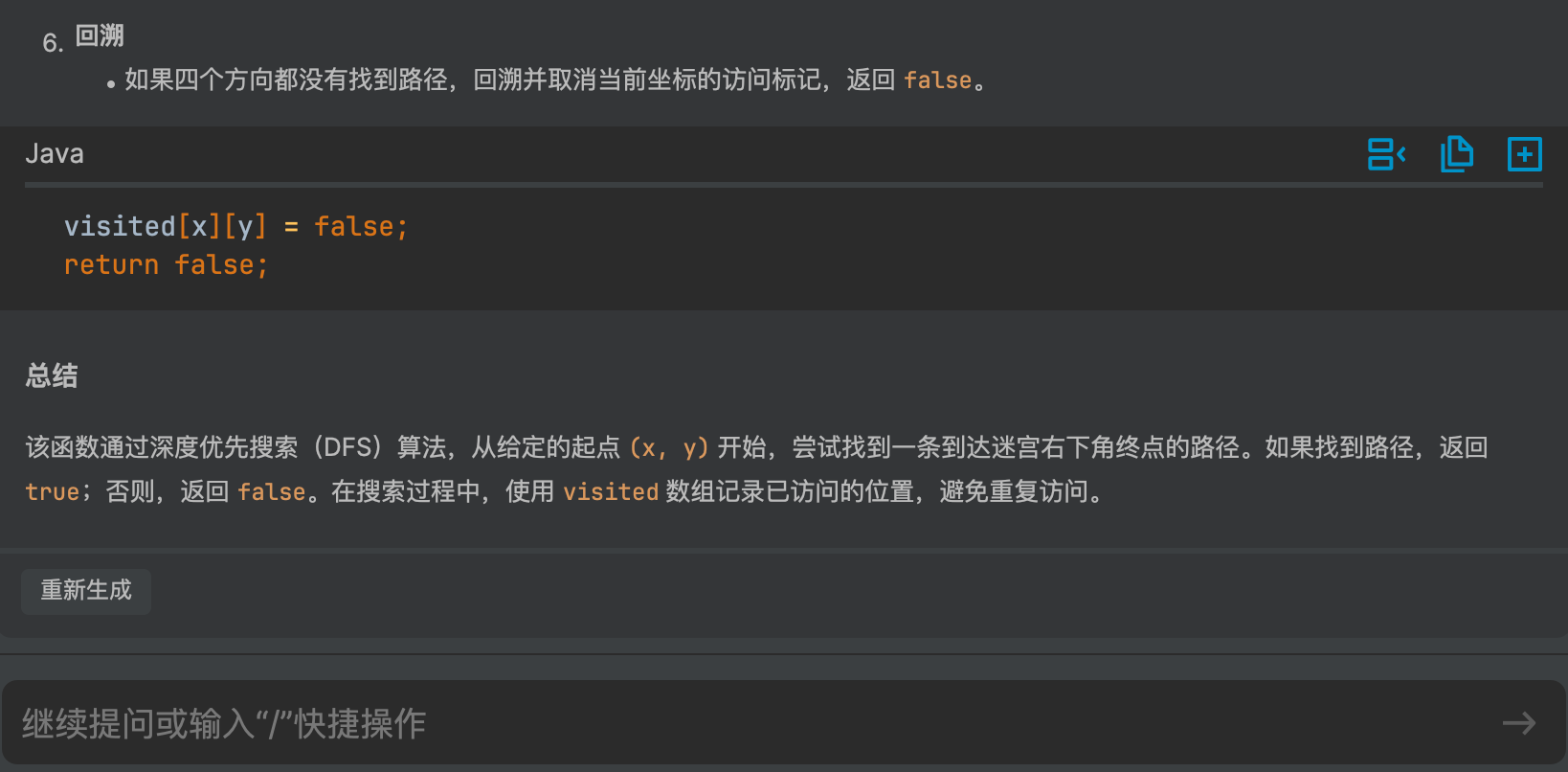
这样生成的代码解释就很详细了,看一下解释的内容对不对,V 哥仔细查看,不放过每一个字,结果堪称完美,你可以试试。
通过通义灵码 AI 工具生成单元测试
通过通义灵码的生成单元测试功能,也是这款AI 工具的亮点,在代码的 dfs 方法的通义灵码图标,选择生成单元测试功能。
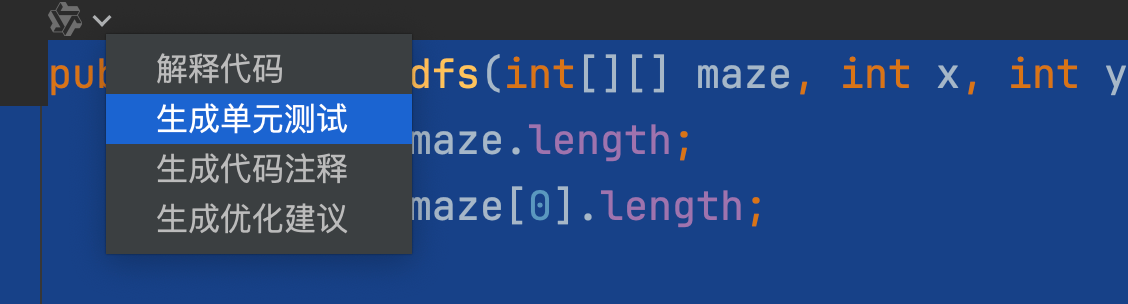
我们就可以在右侧通义灵码的功能区看到生成的测试代码了。
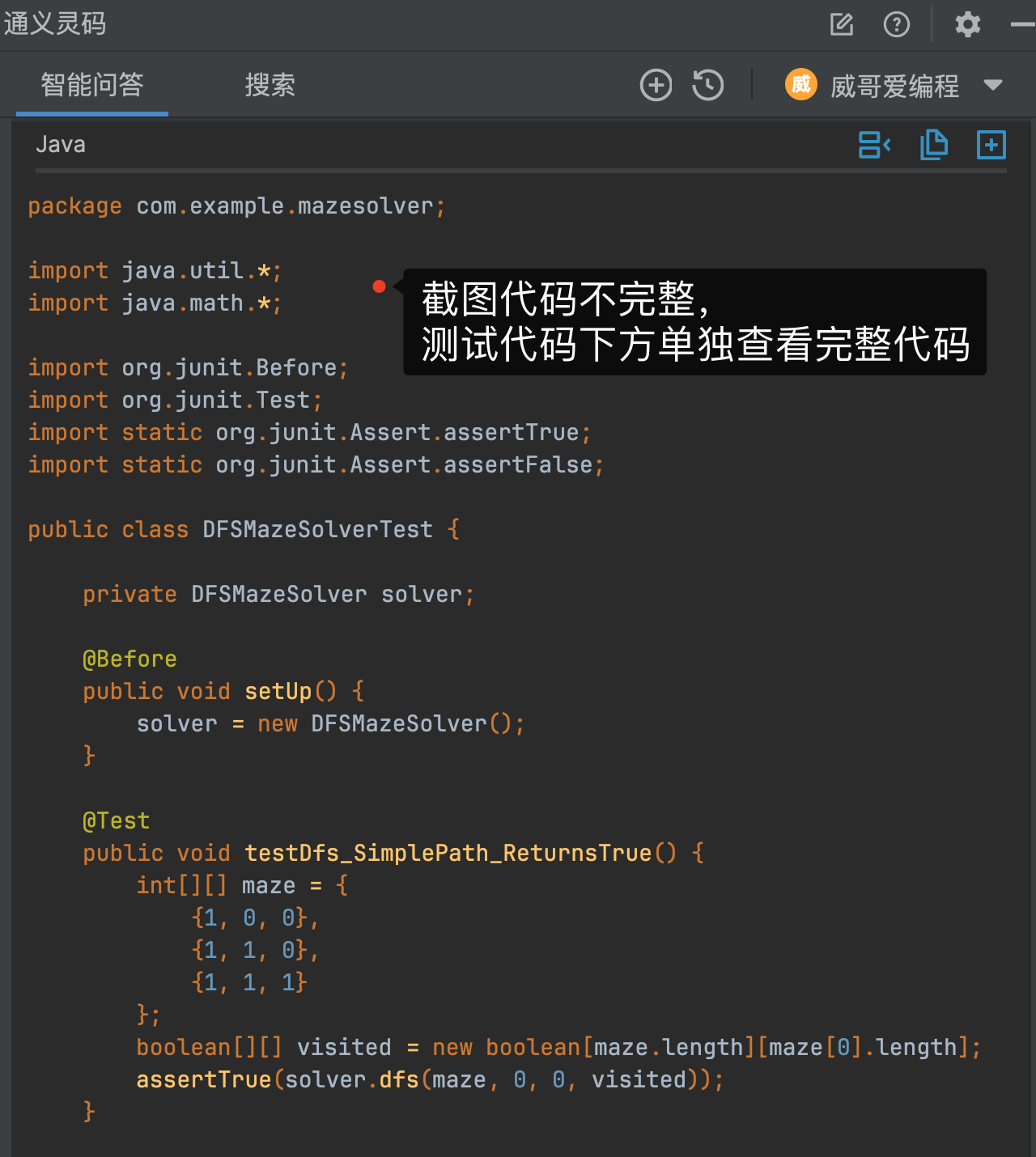
完整生成的测试代码如下:
package com.example.mazesolver;
import java.util.*;
import java.math.*;
import org.junit.Before;
import org.junit.Test;
import static org.junit.Assert.assertTrue;
import static org.junit.Assert.assertFalse;
public class DFSMazeSolverTest {
private DFSMazeSolver solver;
@Before
public void setUp() {
solver = new DFSMazeSolver();
}
@Test
public void testDfs_SimplePath_ReturnsTrue() {
int[][] maze = {
{1, 0, 0},
{1, 1, 0},
{1, 1, 1}
};
boolean[][] visited = new boolean[maze.length][maze[0].length];
assertTrue(solver.dfs(maze, 0, 0, visited));
}
@Test
public void testDfs_NoPath_ReturnsFalse() {
int[][] maze = {
{0, 0, 0},
{0, 0, 0},
{0, 0, 0}
};
boolean[][] visited = new boolean[maze.length][maze[0].length];
assertFalse(solver.dfs(maze, 0, 0, visited));
}
@Test
public void testDfs_AlreadyVisitedCell_ReturnsFalse() {
int[][] maze = {
{1, 0, 0},
{1, 1, 0},
{1, 1, 1}
};
boolean[][] visited = new boolean[maze.length][maze[0].length];
visited[0][0] = true;
assertFalse(solver.dfs(maze, 0, 0, visited));
}
@Test
public void testDfs_MazeTooSmall_ReturnsFalse() {
int[][] maze = {
{0}
};
boolean[][] visited = new boolean[maze.length][maze[0].length];
assertFalse(solver.dfs(maze, 0, 0, visited));
}
@Test
public void testDfs_MazeWithMultiplePaths_ReturnsTrue() {
int[][] maze = {
{1, 1, 0},
{0, 1, 1},
{0, 0, 1}
};
boolean[][] visited = new boolean[maze.length][maze[0].length];
assertTrue(solver.dfs(maze, 0, 0, visited));
}
@Test
public void testDfs_MazeWithDeadEnd_ReturnsFalse() {
int[][] maze = {
{1, 0, 0},
{0, 0, 0},
{0, 0, 1}
};
boolean[][] visited = new boolean[maze.length][maze[0].length];
assertFalse(solver.dfs(maze, 0, 0, visited));
}
}
哇塞,看到代码你是不是跟 V 哥一样的惊叹,我们还可以通过下方的解释代码来帮助你理解测试代码的逻辑和含义。
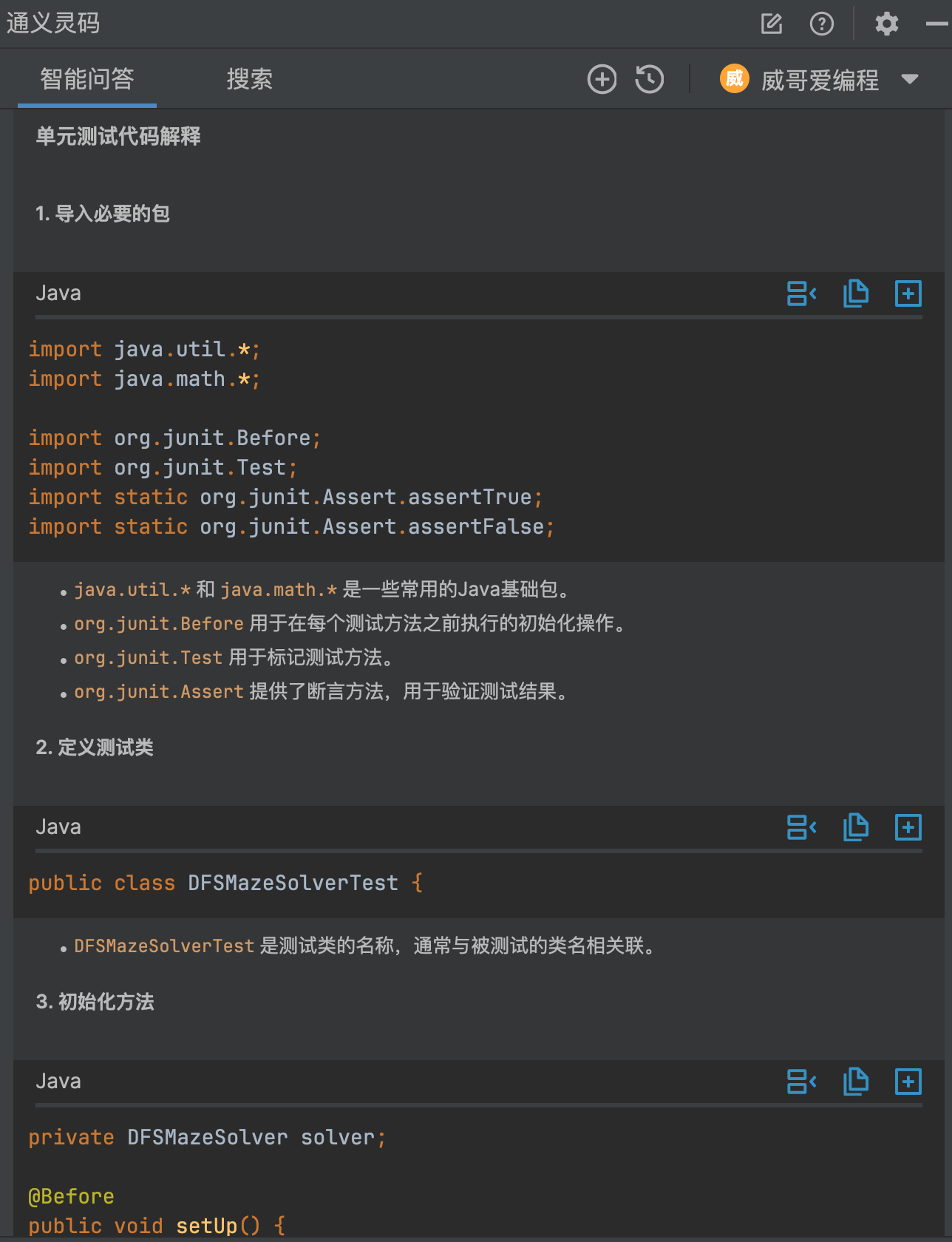
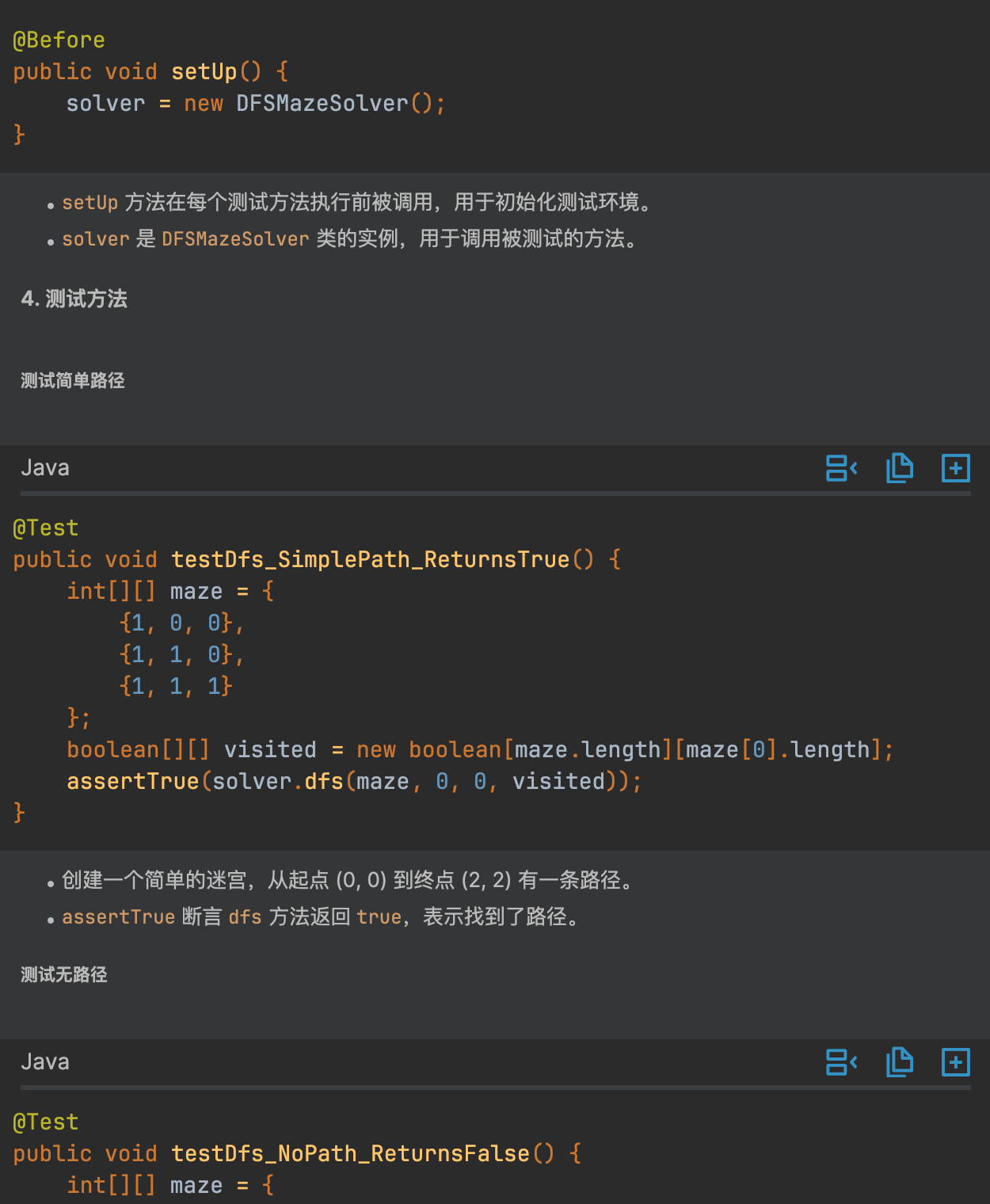
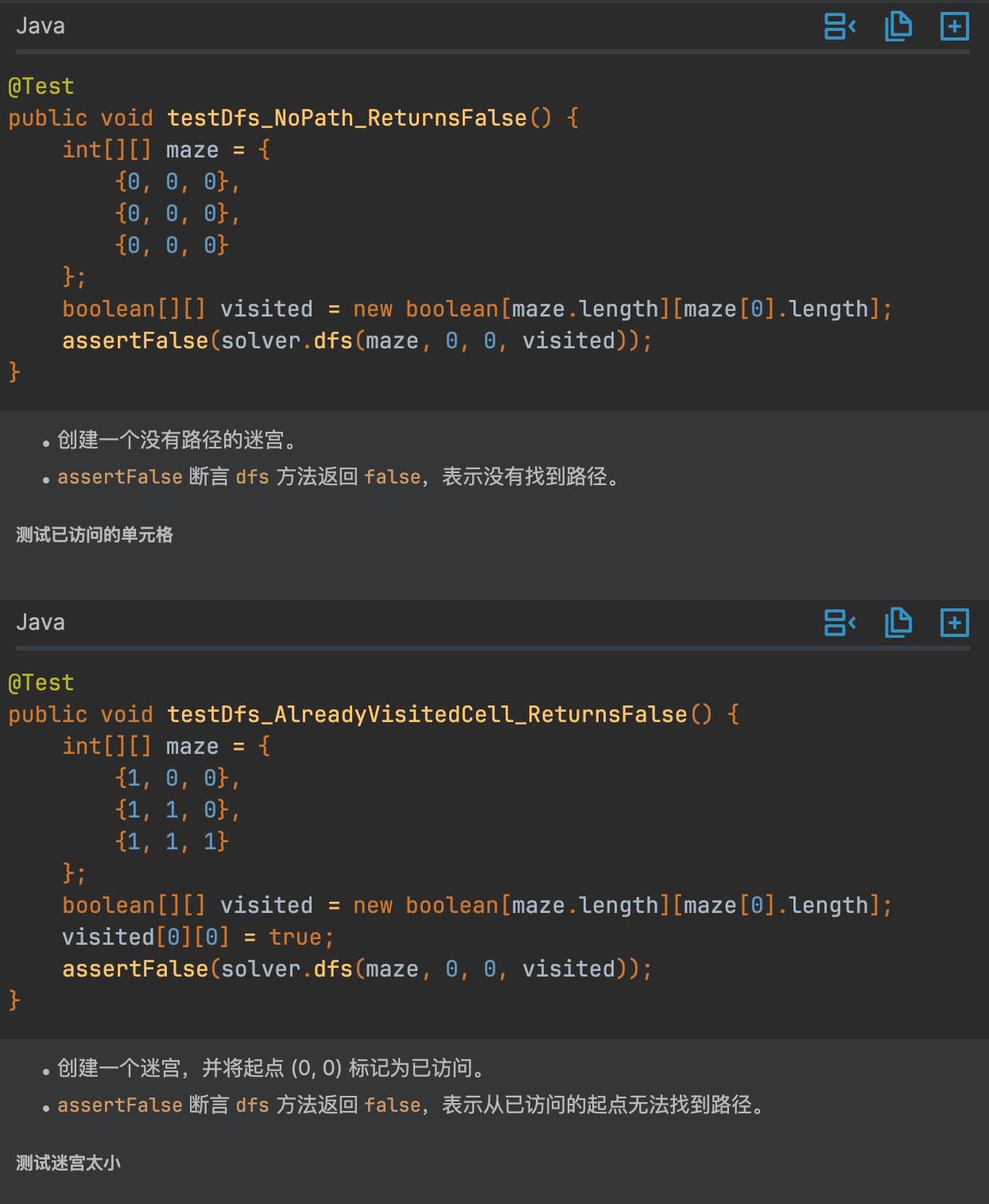
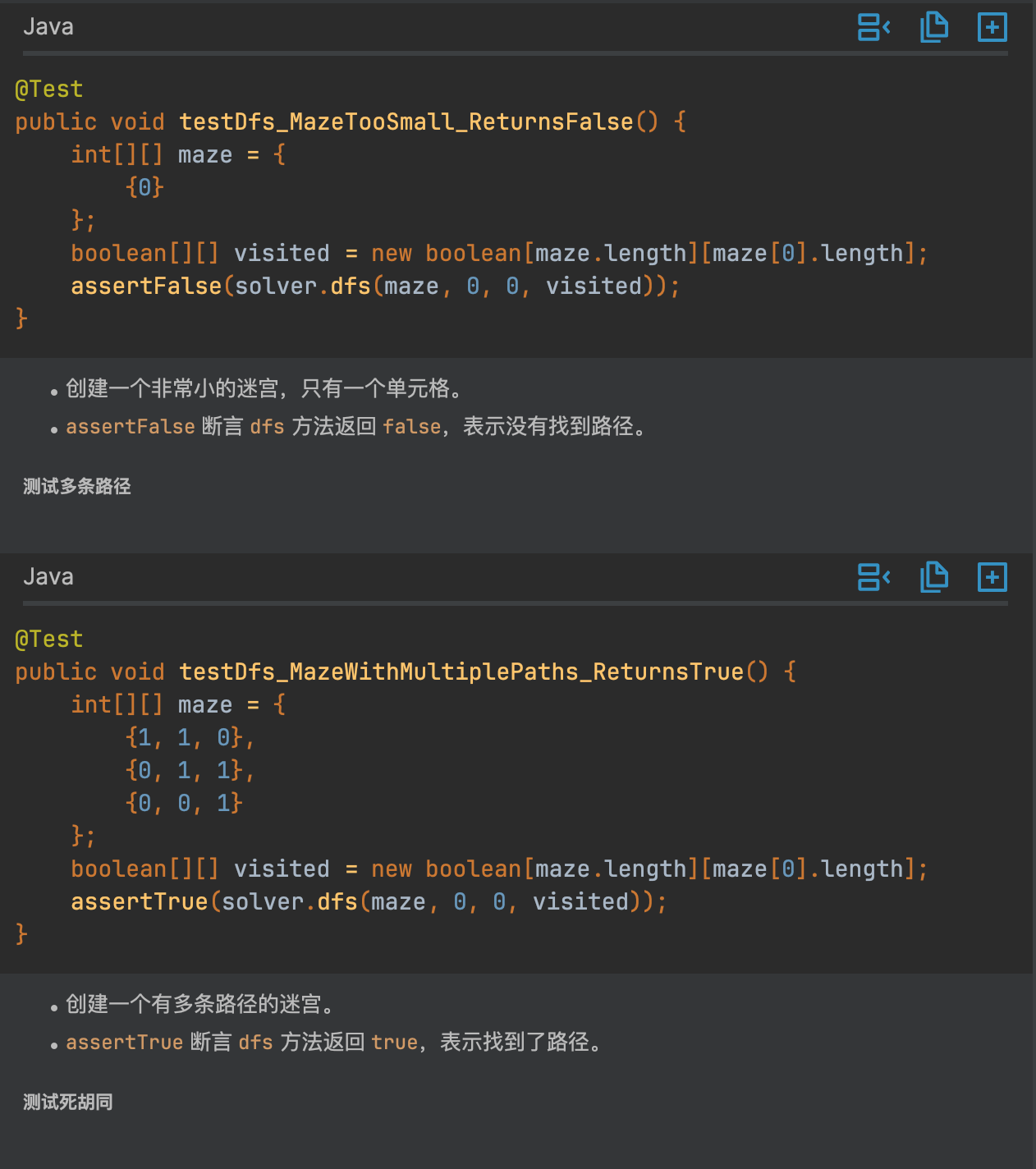
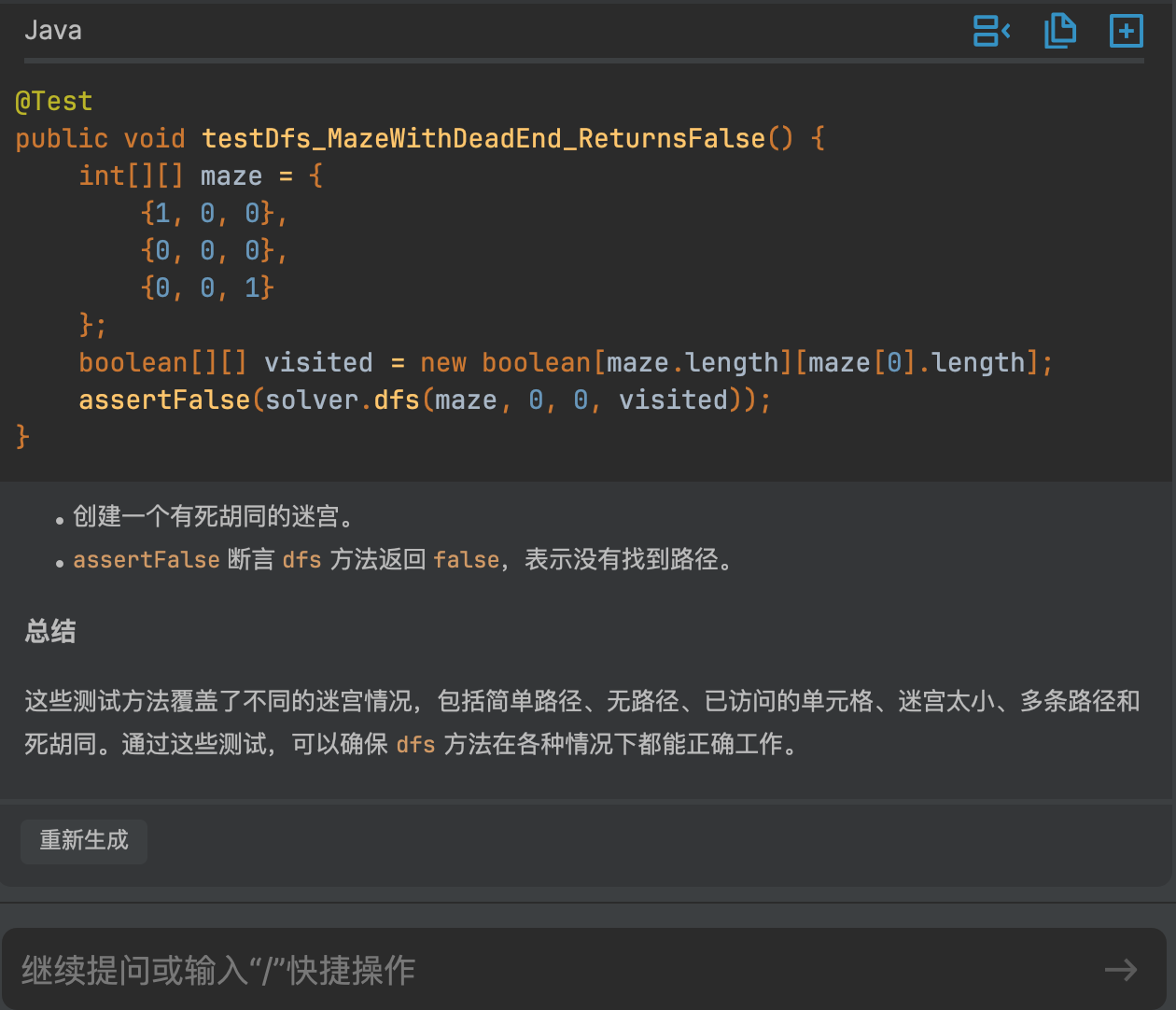
把测试代码拿过来,测试一下看是否可以正常测试代码,结果是没有问题的,在测试中,可以根据自己的需求修改修改就OK 了。
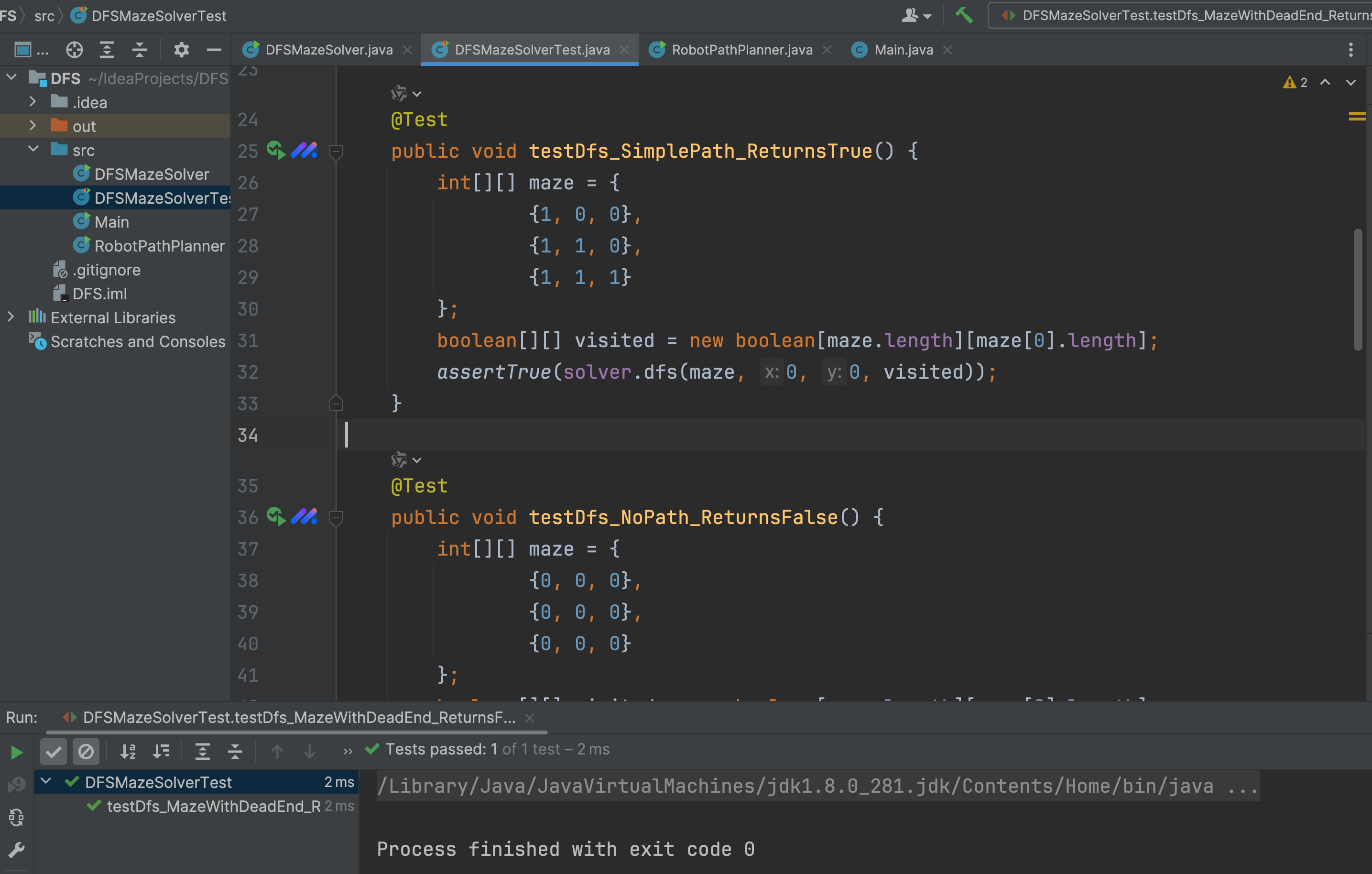
通义灵码生成代码注释功能
通过代码解释功能的使用可以看出,生成代码注释肯定也是 OK 的,功能上貌似有些重复了,这里建议两个功能可以合并一下,比如把类注释的内容也加到解释代码中,把解释好的代码可以在右侧栏中直接一键插入即可。个人建议,当然官方估计看不到我的建议。
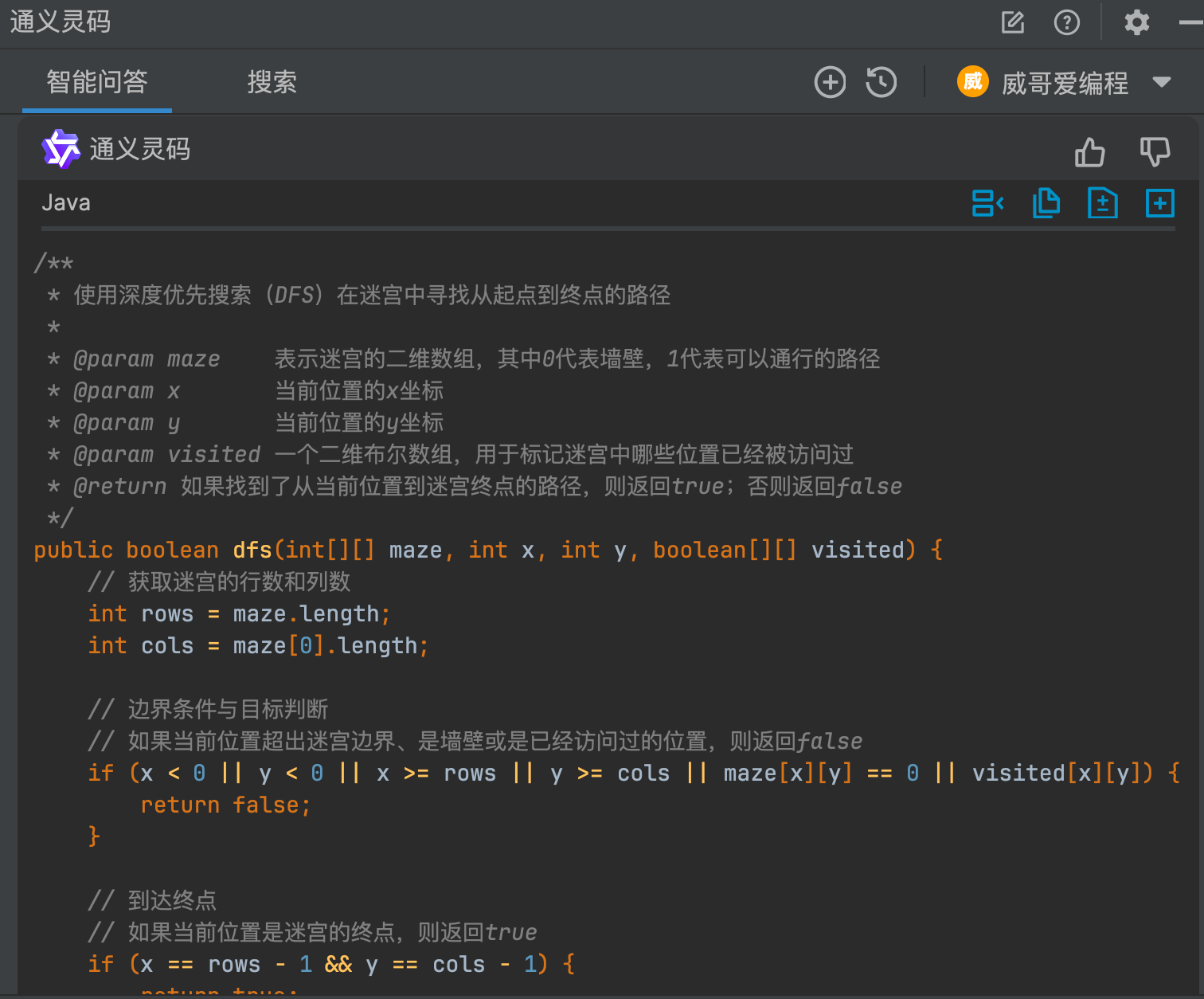
完整的代码注注释如下:
/**
* 使用深度优先搜索(DFS)在迷宫中寻找从起点到终点的路径
*
* @param maze 表示迷宫的二维数组,其中0代表墙壁,1代表可以通行的路径
* @param x 当前位置的x坐标
* @param y 当前位置的y坐标
* @param visited 一个二维布尔数组,用于标记迷宫中哪些位置已经被访问过
* @return 如果找到了从当前位置到迷宫终点的路径,则返回true;否则返回false
*/
public boolean dfs(int[][] maze, int x, int y, boolean[][] visited) {
// 获取迷宫的行数和列数
int rows = maze.length;
int cols = maze[0].length;
// 边界条件与目标判断
// 如果当前位置超出迷宫边界、是墙壁或是已经访问过的位置,则返回false
if (x < 0 || y < 0 || x >= rows || y >= cols || maze[x][y] == 0 || visited[x][y]) {
return false;
}
// 到达终点
// 如果当前位置是迷宫的终点,则返回true
if (x == rows - 1 && y == cols - 1) {
return true;
}
// 标记当前位置已访问
visited[x][y] = true;
// 递归地探索四个方向
// 尝试向四个可能的方向移动,并递归调用DFS如果找到一条路径,则返回true
for (int i = 0; i < 4; i++) {
int newX = x + DX[i];
int newY = y + DY[i];
if (dfs(maze, newX, newY, visited)) {
return true;
}
}
// 回溯
// 如果四个方向都无法到达终点,回溯标记当前位置为未访问,撤销之前的访问标记
visited[x][y] = false;
return false;
}
下面这段与解释代码是一致的:

通义灵码的生成优化建议功能
生成优化建议功能让 V 哥很好奇,通义灵码会给出怎样的建议呢,我们一起来看一下,通义灵码给出了如下建议,并提供了优化后的代码:
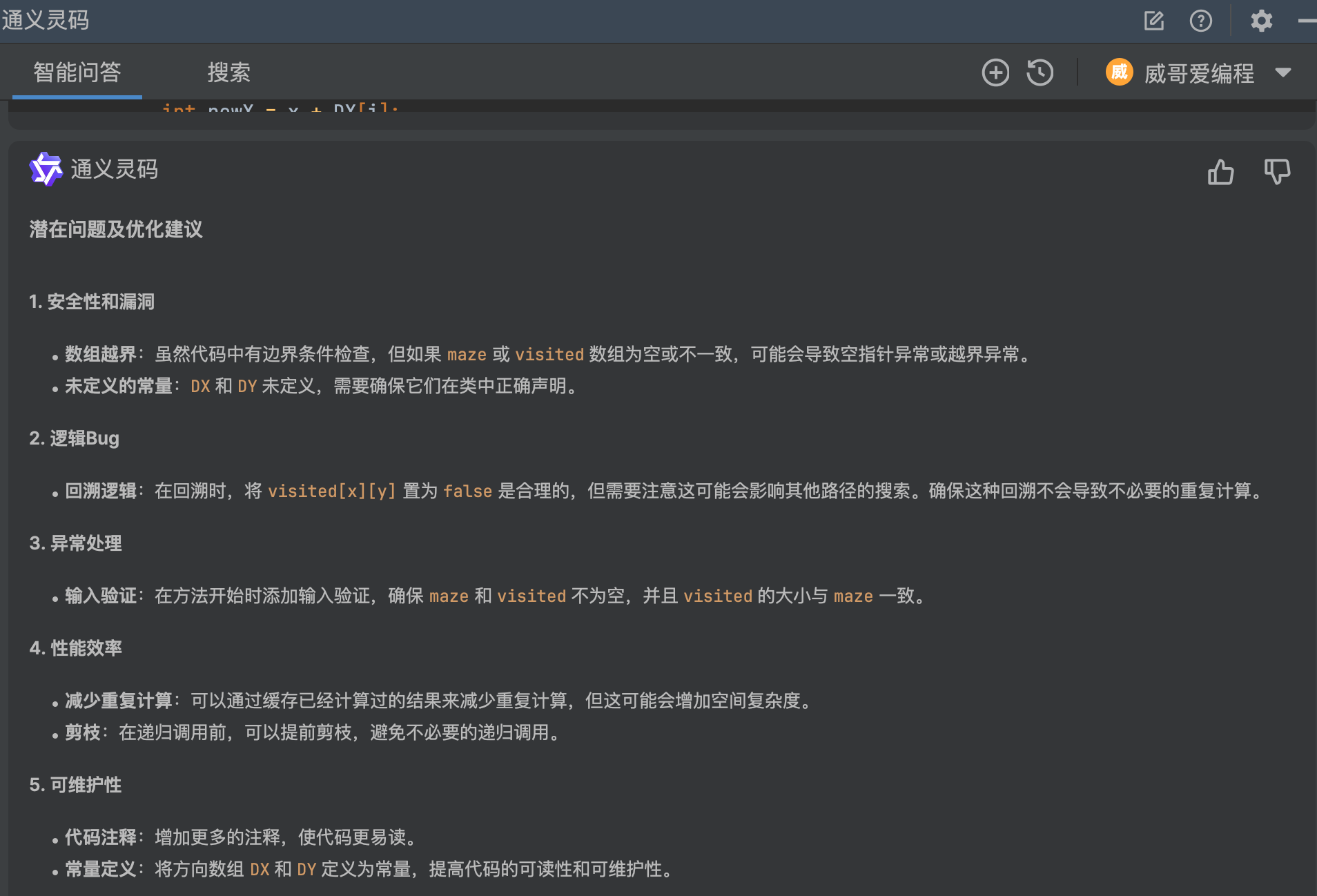
建议修改后的代码如下:
public class MazeSolver {
// 定义方向数组
private static final int[] DX = {1, -1, 0, 0};
private static final int[] DY = {0, 0, 1, -1};
public boolean dfs(int[][] maze, int x, int y, boolean[][] visited) {
// 输入验证
if (maze == null || visited == null || maze.length == 0 || maze[0].length == 0) {
throw new IllegalArgumentException("Invalid input: maze or visited array is null or empty");
}
if (visited.length != maze.length || visited[0].length != maze[0].length) {
throw new IllegalArgumentException("Invalid input: visited array size does not match maze array size");
}
int rows = maze.length;
int cols = maze[0].length;
// 边界条件与目标判断
if (x < 0 || y < 0 || x >= rows || y >= cols || maze[x][y] == 0 || visited[x][y]) {
return false;
}
// 到达终点
if (x == rows - 1 && y == cols - 1) {
return true;
}
// 标记当前位置已访问
visited[x][y] = true;
// 递归地探索四个方向
for (int i = 0; i < 4; i++) {
int newX = x + DX[i];
int newY = y + DY[i];
if (dfs(maze, newX, newY, visited)) {
return true;
}
}
// 回溯
visited[x][y] = false;
return false;
}
}
给出的解释是:
输入验证:在方法开始时添加了对 maze 和 visited 的验证,确保它们不为空且大小一致。
常量定义:将方向数组 DX 和 DY 定义为类的静态常量,提高代码的可读性和可维护性。
注释:增加了注释,使代码更易读。
这些修改不仅提高了代码的安全性和健壮性,还增强了代码的可读性和可维护性。
在通义灵码给出的代码中修改了三处地方,输入验证、常量定义和注释,输入验证和常量定义让 V 哥的代码更加严谨了,在算法实现上没有给出建议,V哥大胆猜测,要不就是V 哥的算法实现已经比较完美了,或者灵码也没有更好的算法优化建议了,哈哈。
通义灵码自动联想代码功能
在编码区写代码时,通义灵码还提供了语义级的自动代码联想功能,这个功能有点奇怪,比如我们在 main 方法中就会建议输出 Hello world:
也许通义灵码想做到想我所想,帮我写代码,由于通义灵码基于通义大模型实现,此功能应该会在学习你的编码习惯和代码意图,如果完全学会了,难道要变成你的克隆吗,还会根据项目中的代码结构来联想,这个功能一旦成熟,那可不得了,期待吧,暂时,V 哥觉得用的还很少。
最后小结一下
总的来说,V 哥在使用通义灵码的过程中,最常用的是解释代码和单元测试的生成,这两部分让我在代码逻辑和测试上大大提高了效率。通义灵码,你有在用吗,欢迎一起交流心得体会。关注威哥爱编程,编码路上我们结伴同行。
本文来自博客园,作者:威哥爱编程,转载请注明原文链接:https://www.cnblogs.com/wgjava/p/18524624





· [翻译] 为什么 Tracebit 用 C# 开发
· 腾讯ima接入deepseek-r1,借用别人脑子用用成真了~
· Deepseek官网太卡,教你白嫖阿里云的Deepseek-R1满血版
· DeepSeek崛起:程序员“饭碗”被抢,还是职业进化新起点?
· RFID实践——.NET IoT程序读取高频RFID卡/标签