医学图像重建 (Medical Image Reconstruction) 学习笔记: (三) 扇形束图像重建

主要参考资料为 《医学图像重建入门》（曾更生，2009）

---

1. 简介

主要介绍扇形束成像的重建算法，包括 *** 等。

在平行光束成像中，我们基于中心切片定理推导出了一些图像重建算法。然而，在扇形束成像中，并没有相应的中心切片定理。通常采用的方法为：把扇形束成像问题转化成平行光束成像问题，然后把平行光束图像重建的算法修正一下，用于解决扇形束的成像问题。

2. 扇形束成像的几何描述及其点扩散函数

在 X 光 CT 领域，其光源多为扇形束的点光源。与平行光束的对比如下：

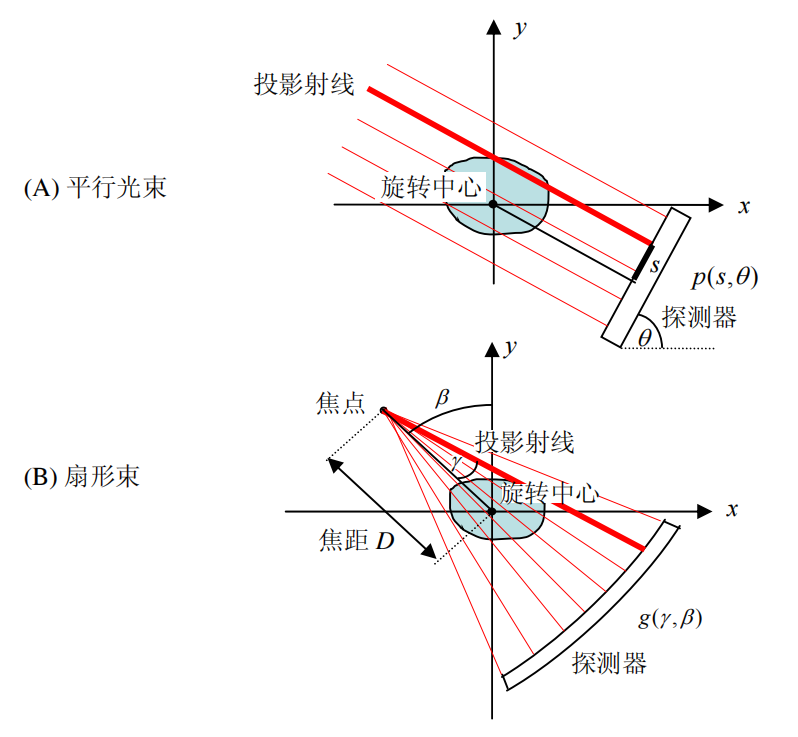
与之前章节相同，我们默认假设探测器是均匀地绕物体转动，且数据采样的角度区间也是均匀的。在这个假设条件下，平行光束的投影/反投影的点扩散函数（PSF）是移动不变的。

在用平行光束成像的情形，为了求反投影在点 \((x, y)\) 的数值，过该点向每个探测方向 \(\theta\) 上的探测器做垂线。把垂线与探测器的交点记为 \(s^*\) 。然后，把投影数值 \(p(s^*, \theta)\) 加到 \((x, y)\) 的位置上。

相似地，在用扇形束成像的情形，为了求反投影在点 \((x, y)\) 的数值，过该点和每个扇形的焦点画一条直线。把该直线与探测器的中线夹角记为 \(\gamma^*\) 。然后把扇形束的投影数值 \(g(\gamma^*, \beta)\) 加到 \((x, y)\) 的位置上。

可以证明，如果扇形束焦点的轨迹是一个完整的圆圈，所得到的投影/反投影的点扩散函数（PSF）是移动不变的。而且，这个投影/反投影的点扩散函数与平行光束成像情形的投影/反投影的点扩散函数是一样的。

（其实这里还是没有特别理解这个“点扩散函数”是什么意思。）

设原本的图像为 \(f(x, y)\) ，经过投影/反投影运算之后得到的图像为 \(b(x, y)\) 。可以证明，投影/反投影的点扩散函数是 \(1/r\) ，其中 \(r = \sqrt{x^2 + y^2}\) 。这样，\(f(x, y)\) 和 \(b(x, y)\) 的关系就建立起来了：

\[b(x, y) = f(x, y)**\frac{1}{r} \]

其中，“**” 表示二维卷积。在傅里叶变换领域，原本图像的傅里叶变换 \(\boldsymbol{F}\) 与投影/反投影运算后的图像的傅里叶变换 \(\boldsymbol{B}\) 的关系是

\[B(\omega_x, \omega_y) = F(\omega_x, \omega_y) \times \frac{1}{\sqrt{\omega^2_x + \omega^2_y}} \]

这是因为 \(1/\sqrt{x^2 + y^2}\) 的二维傅里叶变换是 \(1/\sqrt{\omega^2_x + \omega^2_y}\) 。

我们已经知道，对反投影后的图像 \(b(x, y)\) 进行二维斜坡滤波，即可以重建出原本图像 \(f(x, y)\) 。对于扇形束反投影后的图像 \(b(x, y)\) 完全可以采用同样的方法重建出原本图像 \(f(x, y)\) 。也就是说，线投影后滤波算法对于平行光束成像和扇形束成像是一样的。原本图像 \(f(x,y)\) 的傅里叶变换 \(F(\omega_x, \omega_y)\) 为：

\[F(\omega_x, \omega_y) = B(\omega_x, \omega_y) \times \sqrt{\omega^2_x + \omega^2_y} \]

最后，对 \(F(\omega_x, \omega_y)\) 求二维傅里叶反变换便得到原本图像 \(f(x, y)\) 。

（其实，还是没有特别理解上述过程。）（先做反投影、后做滤波，这很容易理解。但是，滤波函数为什么是这样的形式呢，为什么和平行光束相同呢？）

3. 平行光束算法到扇形束算法的转换

下面对之前介绍的平行光束算法重新推导，将其转化应用到扇形束成像中。