医学图像重建 (Medical Image Reconstruction) 学习笔记: (二) 平行光束图像重建

主要参考资料为 《医学图像重建入门》（曾更生，2009）

---

1. 简介

主要介绍平行光束/射线的图像重建算法，包括 *** 等。

2. 傅里叶变换与希尔伯特变换

2.1 傅里叶变换基本概念理解

对于一个给定的函数 \(p(x)\) ，它总能用不同频率 \(\omega\) 的正弦函数和余弦函数的加权和来表示。这个加权和的权函数记为 \(P(\omega)\) 。这就是傅里叶变换的理论基础。

傅里叶变换的本质是将一个函数按照“进制”分解。比如一堆苹果，它的个数总能以不同的进制下的加权和来表示。比如132个苹果，在十进制下，为 1 个“百（十的二次方）” + 3 个“十（十的一次方）”和 2 个“一（十的零次方）” 表示；在七进制下，为 2 个“七的二次方）”和 4 个“七（七的一次方）” 和 6 个“一（七的零次方）”表示。

（注：进制的形式可以有任意多个形式，但十进制是最便利的之一。基于十进制，形成了诸多“漂亮”的理论形式。同样的道理，“傅里叶变换”也可以有任意多种形式，只是，不同频率 \(\omega\) 的正弦函数和余弦函数的形式下，可以形成诸多最简洁、漂亮的理论公式。因此，这种最有效的变换，就是 傅里叶变换。仍记得在学《量子力学》的时候，某些情况下，应用空间变换/基变换，能够将一些理论公式转化成非常简洁的形式。在此时，也同样是用某些函数作为空间的基向量。同样的道理，我们也是将傅里叶变换中的正弦/余弦函数作为包含任意函数的空间的基向量，那么，任意函数都能记作该空间中的一个点 \(P(\omega)\) 。以上为个人理解。）

（注2：空间的概念是非常神奇的。任何事物（包括函数）都可以对应到空间中的一个点（坐标）。傅里叶变换，其本质就是已知某函数之后，通过公式计算得到“空间”中的坐标值 \(P(\omega)\) 。就好比知道一个点，得到其在笛卡尔空间中的坐标（空间位置）。）

2.2 傅里叶变换与卷积的数学表达

一维傅里叶变换可定义为：

\[P(\omega) = \int^{\infty}_{-\infty} p(s) e^{-2\pi i s \omega} ds \]

相应的一维傅里叶反变换就是：

\[p(s) = \int^{\infty}_{-\infty} P(\omega) e^{2\pi i s \omega} d\omega \]

两个函数 \(f\) 和 \(g\) 的卷积的定义是：

\[(f*g)(t) = \int^{\infty}_{-\infty}f(\tau)g(t-\tau)d\tau = \int^{\infty}_{-\infty}f(t- \tau) g(\tau)d\tau \]

若傅里叶变换的算子记为 \(\boldsymbol{F}\)，傅里叶卷积定理可表述为

\[\boldsymbol{F}(f*g) = \boldsymbol{F}(f) \times\boldsymbol{F}(g) \]

（傅里叶卷积的本质是？？）

2.3 希尔伯特变换与有限希尔伯特变换

傅里叶变换可以把一个实值函数变换成复值函数。而希尔伯特变换只能把一个实值函数变换成另一个实值函数。

用 \(\boldsymbol{H}\) 表示希尔伯特变换的算子。对一个函数 \(f\) 连着实施两次希尔伯特变换就会把这个函数还原，但差一个负号。即

\[\boldsymbol{H}(\boldsymbol{H} f) = \boldsymbol{H}^2 f = -f \]

此外，希尔伯特变换还有如下性质：一个实值函数与其希尔伯特变换是正交的。设 \(g = \boldsymbol{H}f\) ，那么，

\[\int^{\infty}_{-\infty} f(t) g(t) = 0 \]

(其他性质待补充。)

3. 中心切片定理

中心切片定理是断层成像的基础理论。也被程为投影切片定理和傅里叶中心切片定理。该定理指出：二维函数 \(f(x, y)\) 的投影 \(p(s)\) 的傅里叶变换 \(P(\omega)\) 等于函数 \(f(x, y)\) 的傅里叶变换 \(F(\omega_x, \omega_y)\) 沿与探测器平行的方向过原点的片段。

该定理也非常直观，如下图*所示。

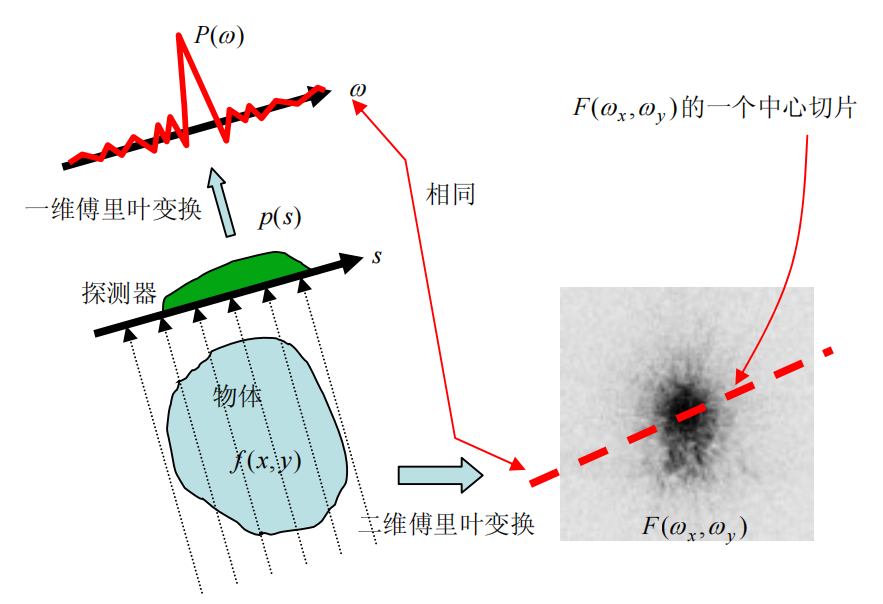
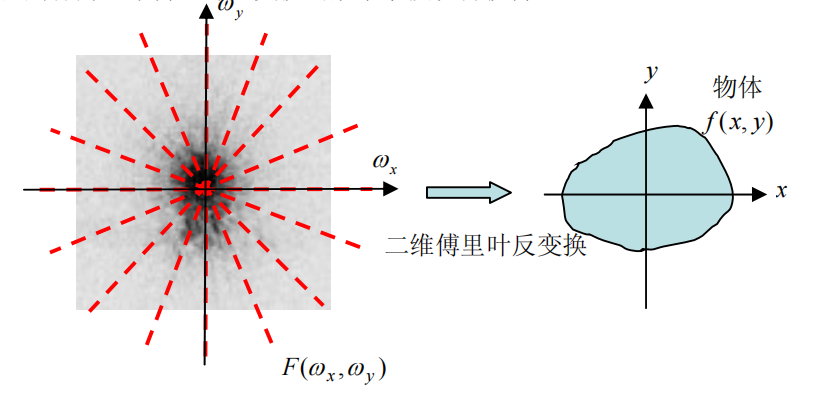
通过观察，我们发现，探测器绕物体旋转 \(180^{\circ}\) 就能探测到完整的傅里叶变换函数 \(F(\omega_x, \omega_y)\) 。如下图*所示。

4. 重建算法

由中心切片定理可知，二维函数 \(f(x, y)\) 的投影 \(p(s)\) 的傅里叶变换 \(P(\omega)\) 等于函数 \(f(x, y)\) 的傅里叶变换 \(F(\omega_x, \omega_y)\) 沿与探测器平行的方向过原点的片段。

换句话说，我们已知各个角度下的投影函数（探测器的值），做傅里叶变换，然后拼接到一起，就能“凑”出二维函数的傅里叶变换 \(F(\omega_x, \omega_y)\) 。那么，再做一次傅里叶反变换，就能得到二位函数 \(f(x, y)\) 了。

但是但是，如上图所示，简单的叠加（即反投影），会导致越靠近中心的位置越“过分叠加”。也就是低频的信息被过分加强了，而高频的信息则被过分减弱了。这将导致图像变得模糊。

做了反投影后，傅里叶空间的密度正比于 \(1/\sqrt{\omega^2_x + \omega^2_y}\)。因此，我们需要对傅里叶空间进行加权矫正，从而消除模糊效果。

第一个方案是，在 \(\omega_x - \omega_y\) 空间，把所得到的傅里叶“图像“乘以 \(\sqrt{\omega^2_x + \omega^2_y}\) ，这个乘积就是 \(F(\omega_x, \omega_y)\) 。对于 \(F(\omega_x, \omega_y)\) 做二维傅里叶反变换得到原本的图像 \(f(x, y)\)。

第二个方案是，把投影数据 \(p(s, \theta)\) 的一维傅里叶变换 \(P(\omega, \theta)\) 乘以 \(|\omega|\) 。然后，再对乘积 \(|\omega| P(\omega, \theta)\) 做一维傅里叶反变换。对投影数据做了处理（滤波）后，再把处理后（即滤波后）的数据做反投影（叠加）。这样就得到了重建的图像 \(f(x, y)\) 。本方案通常被称作 FBP (Filtered Backprojection) 算法，\(|\omega|\) 被称为斜坡滤波器。

下面，将具体介绍其中的各种，细节及技巧组合。每种算法都有其长处和短处。

4.1 方法1 （先滤波再反投影，Filtered Backprojection, FBP 算法）

在 Filtered Backprojection (FBP) 算法中，其具体步骤为：(i) 先求投影数据 \(p(s, \theta)\) 的傅里叶变换，得到 \(P(\omega, \theta)\) ；(ii) 接下来，将其乘以斜坡滤波器的传递函数 \(|\omega|\) ，得到 \(Q(\omega) = P(\omega, \theta) \times H(\omega)\) ；(iii) 求 \(Q(\omega, \theta)\) 的傅里叶反变换 \(q(s, \theta)\)，(iv) 最后，进行反投影得到 \(f(x, y)\) 。

4.2 方法2

与上述方法相同，需要先进行滤波。只是，根据傅里叶变换理论，在 \(\omega\) 域做乘法等价于在 \(s\) 域做卷积。因此，我们不需要“傅里叶变换、相乘、傅里叶反变换”这样复杂，可以直接做卷积，如下：

\[Q(\omega) = P(\omega, \theta) \times H(\omega) \quad \rightarrow \quad q(s, \theta) = p(s, \theta) * h(s) \]

这里，* 是卷积运算记号。\(h(s)\) 是卷积积分中的卷积核，它是 \(H(\omega) = |\omega|\) 的一维傅里叶反变换。

4.3 方法3 （求导、希尔伯特变换、反投影， Derivative，Hilbert transform，Backprojection，DHB 算法）

在方法1中，是在 \(\omega\) 域做乘法。其中，斜坡滤波器的传递函数可以拆分为：

\[H(\omega) = |\omega| = i2\pi\omega \times \frac{1}{2\pi} \times (-i \text{sgn}(\omega)) \]

(注，实际上就是分子、分母都添加了 \(i2\pi\) ，sgn 是表示正负号的。)

已知傅里叶变换的两个性质：（1）在傅里叶域（即 \(\omega\) 域）中乘以 \(i2\pi\omega\) 就相当于在空间域（即 \(s\) 域）中求导数；（2）函数 \(-i\text{sgn}(\omega)\) 的傅里叶反变换是 \(1/(\pi s)\) 。与 \(1/(\pi s)\) 做卷积又叫做希尔伯特变换。

由上述两个性质、以及传递函数的拆分，可以将上述 FBP 算法推导为：

\[Q(\omega) = P(\omega, \theta) \times H(\omega) = P(\omega, \theta) \times i2\pi\omega \times \frac{1}{2\pi} \times (-i \text{sgn}(\omega)) \]

其中，上述公式前两项的傅里叶反变换为：

\[P(\omega, \theta) \times i2\pi\omega \rightarrow \frac{dp(s, \theta)}{ds} \]

上述公式的最后一项的傅里叶反变换为：

\[-i \text{sgn}(\omega) \rightarrow \frac{1}{\pi s} \]

那么，上述 \(Q(\omega)\) 的傅里叶反变换为

\[q(s, \theta) = \frac{dp(s, \theta)}{ds} * \frac{1}{2\pi^{2}s} \]

也就是说，方法1中的算法还可以转化为求导和希尔伯特变换的组合来完成。

4.4 方法4

在上述方法中，都是先对投影数据（或其傅里叶变换）进行滤波，然后再反投影。我们当然也可以先做反投影，再做滤波。具体如下：(i) 反投影得到图像 \(b(x, y)\) ；(ii)对反投影得到的图像做二维傅里叶变换，得到 \(B(\omega_{x}, \omega_{y})\) ；(iii) 对 \(B(\omega_{x}, \omega_{y})\) 进行滤波，乘以斜坡滤波器的传递函数 \(|\omega| = \sqrt{\omega^{2}_{x} + \omega^{2}_{y}}\) ，得到 \(F(\omega_{x}, \omega_{y})\) ；(iv) 对其进行傅里叶反变换，得到 \(f(x, y)\) 。

4.5 方法5 （求导、反投影、希尔伯特变换， Derivative，Backprojection，Hilbert transform，DBH 算法）

在方法3中，是求导、希尔伯特变换、反投影三个过程。我们也可以改变一下他们的顺序，即：(i) 先求导，对投影数据 \(p(s, \theta)\) 以变量 \(s\) 求导（实际上是求偏导），得到 \(dp(s, \theta)/ds\) ；(ii) 对 \(dp(s, \theta)/ds\) 做 \(180^{\circ}\) 的反投影；(iii) 对反投影得到的图像逐行的做（一维的）希尔伯特变换。其方向是与探测器在 \(90^{\circ}\) 角的位置相平行。

（注：感觉跟方法3好像也没啥区别啊。）

5. 利用截断的投影数据重建 ROI

如果我们只对图像中的一个小区域感兴趣，这个小区域叫 ROI (Rgeion of Interest，感兴趣区域)。在一些特定情形中，完全有可能用截断的（不完整的）投影数据做准确的 ROI 重建。在断层成像理论中，这个 ROI 重建问题叫做 内部重建问题（Interior Problem）。一般而言，内部重建问题只能得到近似解，只有在一些特殊条件下才能得到精确解。

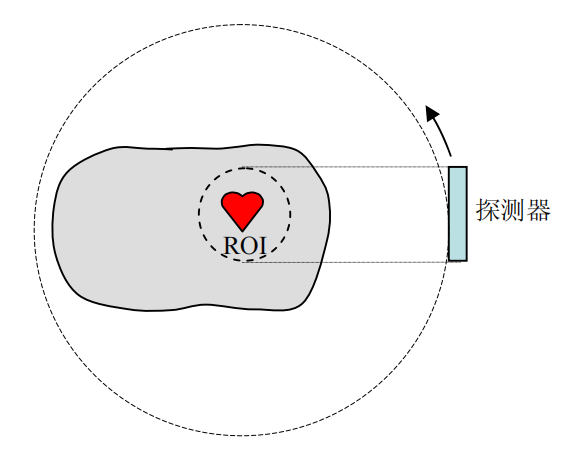
内部重建问题可以通过 DBH (Derivative，backprojection，and the Hilbert transform 求导，反投影，及希尔伯特变换，上述方法5）算法来进行重建。（其中需要使用有限的希尔伯特发变换实现。）

（进一步的细节待补充。）

6. 小结

主要介绍了平行投影数据的重建算法。