医学图像重建 (Medical Image Reconstruction) 学习笔记: (一) 断层成像基本原理

主要参考资料为 《医学图像重建入门》（曾更生，2009）

---

1. 断层成像

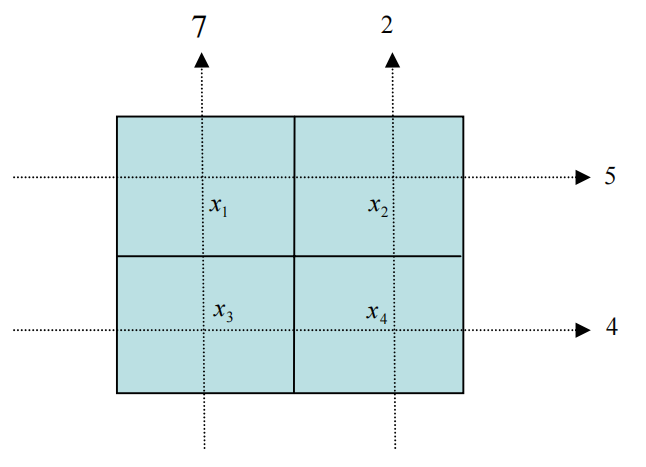
断层成像可以理解为 “根据射线穿透物体后的结果反推物体内部的影像”。其过程是一个数学问题。如下图1所示，投影的过程为，射线沿某个方向（如从左至右、从下到上）穿过物体，穿过各个元素后数值累加，则有:

\[x_1 + x_2 = 5, \quad x_3 + x_4 = 4, \quad x_1 + x_3 = 7, \quad x_2 + x_4 = 2 \]

对上述方程组求解，就可以得到物体内部的成像 (各个元素的值)，即

\[x_1 = 3, \quad x_2 = 2, \quad x_3 = 4, \quad x_4 = 0 \]

由此可见，在断层成像中，射线穿过物体、传感器采集信号，是一个数值累加的过程，得到了一系列方程组。通过某些手段/方法，求解该方程组（或者是得到了方程组的近似解），便得到了物体内部的成像（重建过程）。

2. 投影

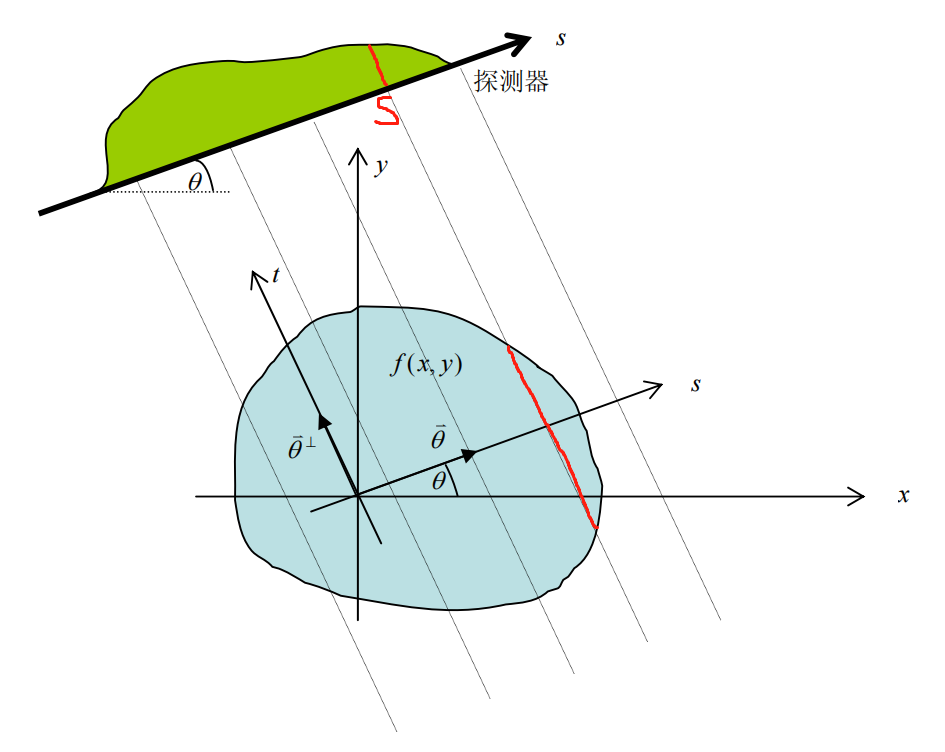
如前所述，投影的过程为，射线沿某个方向穿过物体，所穿过的各个元素数值累加。如下图2所示，物体位于坐标系 \(xOy\) 中，其内部密度为 \(f(x, y)\) ，一组平行射线穿过物体。探测器位置如图所示，与 \(x\) 轴成夹角 \(\theta\) 。在探测器的 \(s\) 位置上，射线穿透物体后累积的值（射线和、线积分）为：

\[p(s, \theta) = \int^{+\infty}_{-\infty}\int^{+\infty}_{-\infty} f(x, y)\delta(x\cos\theta + y\sin\theta - s)dxdy \]

如下图*所示，考虑 \(\theta\) 和 \(s\) 处，射线穿过的路径为下方红线。红线的方程即为 \(x\cos\theta + y\sin\theta -s =0\) 。然后，通过 \(\delta\) 函数和积分的方式，完成线积分/投影。

如下图*所示，左上方红线是在 \(\theta\) 和 \(s\) 处的值。当 \(s\) 取 \([-min, +max]\) 时，组成了下图中的一条曲线（绿色部分）。在实际应用中，\(\theta\) 为一系列离散的值（对应于不同角度下测量得到的值），将得到的一系列的曲线。

此外，投影函数还有不同的等价表达式，例如：

\[p(s,\theta) = \int^{+\infty}_{-\infty}\int^{+\infty}_{-\infty} f(x, y)\delta(\vec{x} \cdot \vec{\theta} - s)dxdy \]

\[p(s,\theta) = \int^{+\infty}_{-\infty} f(s \cos \theta - t \sin \theta, s \sin \theta + t \cos \theta)dt \]

其中，\(\delta\) 是狄拉克函数。

3. 反投影

3.1 简单描述

首先必须指出，反投影运算并不是投影运算的逆运算。用数学语言说，反投影算子不是投影算子的逆算子。仅仅靠反投影是不能重建图像的。

所谓反投影，是通过直接观察后得到的一种简便方法。尽管反投影图像和原本图像并不相同，但他们之间有着密切联系。

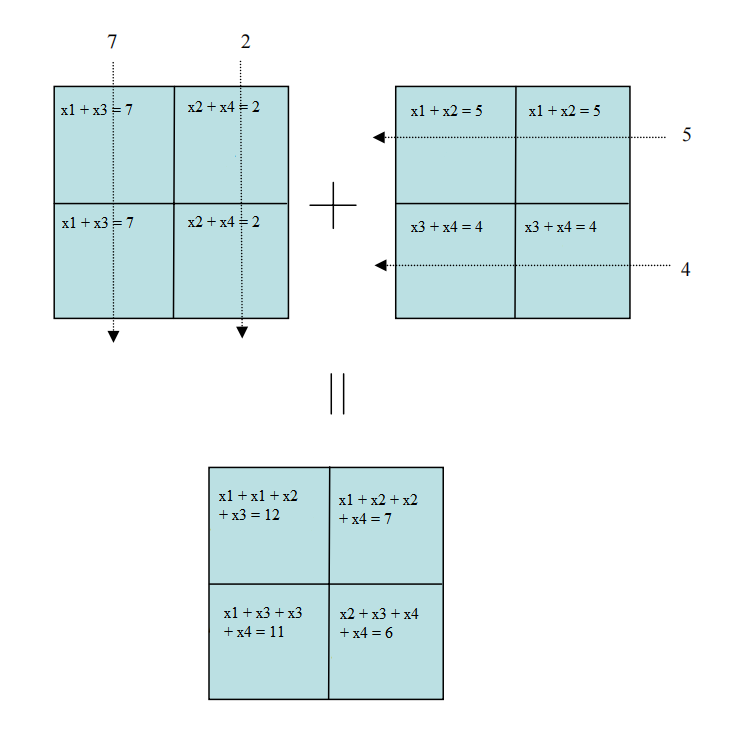
如下图所示，分别做反投影，然后叠加。得到的结果中，各个元素自身的值是2倍，其他元素（干扰、噪声）是1倍。这样就能近似得到原始物体各个元素的值。如果增加投影角度，越能接近原始值，但貌似干扰（噪声）也会越大。

3.2 数学描述

反投影算子是投影算子的伴随算子。在上述章节中，讨论的离散投影问题，它可以描述为矩阵的乘积：

\[P = AX \]

其中，\(X\) 是用列向量（即列矩阵）的形式表达一个图像。对于一个 2
x2 的图像来说，它的列向量为

\[X = [x_1, x_2, x_3, x_4]^T \]

上述列矩阵 \(P\) 代表投影数据。如果用上述例子，这个列矩阵 \(P\) 就是

\[P = [p(1, 0^{\circ}), p(2, 0^{\circ}), p(1, 270^{\circ}), p(2, 270^{\circ})]^{T} = [7, 2, 5, 4]^T \]

矩阵 \(A\) 实际上是投影算子。其矩阵元素 \(a_{ij}\) 实际上就是射线通过的路径相关，即

\[A = \begin{bmatrix}1 &0 &1 &0\\ 0 &1 &0 &1 \\ 1 &1 &0 &0 \\ 0 &0 &1 &1\end{bmatrix}\]

对于连续情况，反投影图像 \(b(x, y)\) 有以下集中等价的表达式：

\[b(x, y) = \int^{\pi}_{0}p(s, \theta)|_{s = x\cos\theta + y \sin\theta} d\theta \]

4. 狄拉克函数

狄拉克 \(\delta\) 函数实际上是一个广义函数（或称为分布函数），它可以用不同的方式来定义。这里，我们用一个高斯函数序列来定义它。当参数 \(n\) 增大时，曲线变得越来越窄，而且越来越高：

\[(\frac{n}{\pi})^{(1/2)}e^{-nx^2} \]

狄拉克 \(\delta\) 函数有如下性质：

\[\int^{\infty}_{-\infty}\delta(x-a)f(x)dx = \int^{\infty}_{-\infty}\delta(x)f(x+a)dx = f(a) \]

\[\int^{\infty}_{-\infty}\delta(ax)f(x) dx = \frac{1}{|a|} f(0) \]

\[\int^{\infty}_{-\infty}\delta^{(n)}(x)f(x)dx = (-1)^{n}f^{(n)}(0) \quad \text{[第 $n$ 阶导数]} \]

\[\delta(g(x))f(x) = \sum_{n} \frac{1}{|g'(\lambda_{n})|} \delta(x - \lambda_{n}), \quad \text{其中 $\lambda_{n}$ 为 $g(x)$ 的零点。} \]

狄拉克 \(\delta\) 函数的诸多性质将会在后续 Filtered Back Projection 方法中用到。

5. 小结

简要介绍了医学影像重建的入门概念等。