论文阅读笔记：Complementary Dynamics

论文题目：Complementary Dynamics 。It is a SIGGRAPH Asia 2020 paper by Jiayi Eris Zhang, Seungbae Bang, David I.W. Levin and Alec Jacobson. More details is in the Project Page

---

0. 摘要

论文提出了一种

1. 背景

为了实现****

2. 方法初探

首先，定义仿真所涉及的变量。定义骨架参数 rig parameter 为 $\mathit{p}\in {\mathbb{R}}^m$ ；基于骨架蒙皮结构，由骨架偏移实现的网格节点位移为 ${\mathit{u}}^r$ ；基于本文所提出的方法，计算得到的 complementary displacement 网格节点位移为 ${\mathit{u}}^c$ ；在 $t$ 时刻，网格节点的位移是两者相加的和，即

$${\mathit{u}}_t={\mathit{u}}_t^r+{\mathit{u}}_t^c$$

在软体对象的形变仿真中，可基于优化隐式积分方法进行求解计算。 $t$ 时刻网格节点的位移为如下非线性最优化问题 non-linear optimization problem 的解，即

$${\mathit{u}}_t=argmin{E}_t({\mathit{u}}_t)$$

其中，$E_t$ 是能量函数，包括了弹性势能 potential energy 、动能 momentum term ，外力做功 external work 等，即

$$E_t({\mathit{u}}_t)=\mathrm{\Phi }({\mathit{u}}_t)+\frac{1}{2h^2}{\ddot{{\mathit{u}}_t}}^T\mathit{M}\ddot{{\mathit{u}}_t}-{\mathit{u}}_t^T\mathit{f}({\mathit{u}}_t)$$

其中，$h>0$ 是仿真时间步长；$\mathit{M}\in {\mathbb{R}}^{dn\times dn}$ 是质量矩阵 mass matrix 。

那么，在本论文的仿真计算中，complementary displacement 网格节点位移 ${\mathit{u}}_t^c$ 可通过求解上述优化问题得到，（注：${\mathit{u}}_t^r$ 是已知量），即

$${\mathit{u}}_t^c=argmin{E}_t({\mathit{u}}_t^r+{\mathit{u}}_t^c)$$

思考：对上述问题直接求解，得到的结果将会是 ${\mathit{u}}_t^c=-{\mathit{u}}_t^r$ ，也就是会 undo the rig displacements ，显然是不对的。因此，在仿真计算中，应加入适当约束，对 complementary displacement ${\mathit{u}}_t^c$ 施加一定的限制。

3. 骨架正交约束 Rig Orthogonality Constraints

接下来思考如何定义约束。换一个视角，如果 ${\mathit{u}}_t^c$ 和 ${\mathit{u}}_t^r$ 互不相关，那么，给定当前的骨架参数 ${\mathit{p}}_t$ ，对于任意有效的 ${\mathit{u}}_t^c$ 都应满足如下标准，即

$$argmin\frac{1}{2}||{\mathit{u}}^r({\mathit{p}}_t)+{\mathit{u}}_t^c-{\mathit{u}}^r(\mathit{p})|{|}_{\mathit{M}}^2={\mathit{p}}_t$$

其中，$||\mathit{x}|{|}_{\mathit{M}}^2={\mathit{x}}^T\mathit{M}\mathit{x}$ 。该约束将保证 ${\mathit{u}}_t^c$ 和 ${\mathit{u}}_t^r$ 互不相关。
（上面这一段的表述，还需要再整理，感觉没讲清楚）

有了上述条件，我们取优化目标函数的一阶导数，即

$$\frac{\partial \frac{1}{2}||{\mathit{u}}^r({\mathit{p}}_t)+{\mathit{u}}_t^c-{\mathit{u}}^r(\mathit{p})|{|}_{\mathit{M}}^2}{\partial \mathit{p}}{|}_{{\mathit{p}}_t}=0$$

将上述公式拆分，得到

$$\frac{\partial ({\mathit{u}}^r({\mathit{p}}_t)+{\mathit{u}}_t^c-{\mathit{u}}^r(\mathit{p}))}{\partial \mathit{p}}{|}_{{\mathit{p}}_t}^T\mathit{M}({\mathit{u}}^r({\mathit{p}}_t)+{\mathit{u}}_t^c-{\mathit{u}}^r(\mathit{p}))=0$$

由于 ${\mathit{u}}^r({\mathit{p}}_t)$ 以及 ${\mathit{u}}_t^c$ 均与 $\mathit{p}$ 无关，对其偏导数为零，上述公式进一步简化为

$$\frac{\partial {\mathit{u}}^r}{\partial \mathit{p}}{|}_{{\mathit{p}}_t}^T\mathit{M}{\mathit{u}}_t^c=0$$

其中，${\mathit{J}}_t^T=\frac{\partial {\mathit{u}}^r}{\partial \mathit{p}}{|}_{{\mathit{p}}_t}^T$ 为骨架的雅可比矩阵 rig Jacobian matrix 。

上述约束意味着，${\mathit{u}}^c$ 与骨架蒙皮的位移正交互补: This constraint can read as requiring that ${\mathit{u}}^c$ lies in the orthogonal complement of the rig, first order.

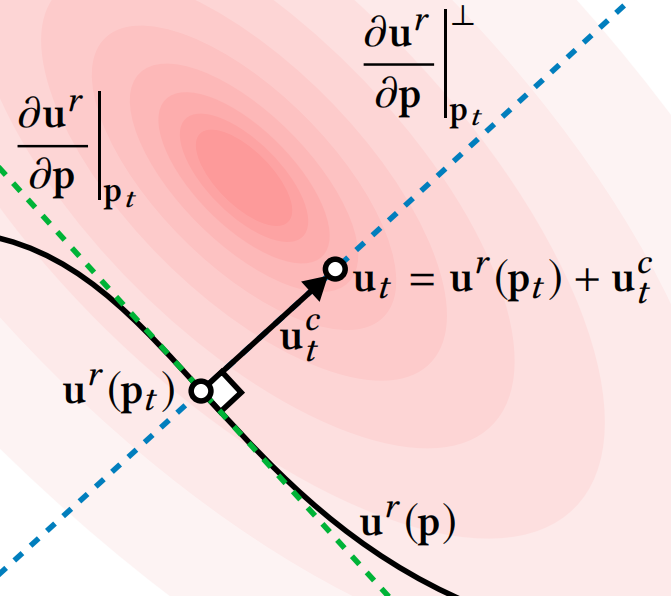
4. 约束仿真 Constrainted Simulation

基于上述骨架正交约束，可以重新给出形变仿真的优化问题，即

$${\mathit{u}}_t^c=argmin{E}_t({\mathit{u}}_t^r+{\mathit{u}}^c)\text{subject to}{\mathit{J}}_t^T\mathit{M}{\mathit{u}}^c=0$$

对于上述优化问题的求解，通常可采用拉格朗日乘子法，即上述优化问题可转化为如下线性系统：

$$\left[\begin{array}{cc}\mathit{Q}& {\mathit{C}}^T\\ \mathit{C}& \mathbf{0}\end{array}\right]\left[\begin{array}{c}\mathit{x}\\ \lambda \end{array}\right]=\left[\begin{array}{c}\mathit{l}\\ \mathbf{0}\end{array}\right]$$

其中，$\mathit{Q}={\partial }^2\mathrm{\Phi }/\partial {{\mathit{u}}^C}^2+h^{-2}\mathit{M}$，是与 Hessian 矩阵相关的项；$\mathit{l}=-\partial \mathrm{\Phi }/\partial {\mathit{u}}^C+\frac{\mathit{M}}{h^2}({\mathit{u}}_t^r-{\mathit{u}}_{t-h}-h{\dot{\mathit{u}}}_{t-h})+{\mathit{f}}_t$，是 Gradient 相关的项；$\mathit{C}={\mathit{J}}_t^T\mathit{M}$，是骨架 Jacobian 相关的项。

5. 优化问题求解 Newton-Raphson方法

采用拉格朗日乘子法对上述优化问题求解，最终转化为非线性方程组 $\mathit{A}\mathit{x}=\mathit{b}$ 。在本文中，采用了 Newton-Raphson 方法对该非线性方程组进行求解。结合 Newton-Raphson方法求解多元非线性方程组 中给出的介绍，求解流程如下：

1、初始化。计算 rig 分量 ${\mathit{u}}_t^r$，计算初始位移 ${\mathit{u}}^{(0)}$，complementary 分量为零，即 ${\mathit{u}}^{c(0)}=\mathbf{0}$ ；最大迭代次数为 $N=20$ ；置 $k=0$；精度要求为 $ϵ=1e^{-6}$

2、求解方程组 $\mathit{A}({\mathit{x}}^{(k)})\mathit{d}=-\mathit{F}({\mathit{x}}^{(k)})$

注：Newton-Raphson方法求解多元非线性方程组参见 Newton-Raphson方法求解多元非线性方程组