（一）泛函的概念

泛函的定义

定义一： 泛函（functional）通常是指定义域为函数集，而值域为实数或者复数的映射。换而言之，泛函是从由函数组成的一个向量空间到标量域的映射。

定义二： 设 \(\boldsymbol{C}\) 是函数（形式）的集合，\(\boldsymbol{B}\) 是实数集合；如果对 \(\boldsymbol{C}\) 中的任一个元素 \(y(x)\)，在 \(\boldsymbol{B}\) 中都有一个元素 \(\boldsymbol{J}\) 与之对应，则称 \(\boldsymbol{J}\) 为 \(y(x)\) 的泛函，记为 \(\boldsymbol{J}[y(x)]\)。

这里的函数集合，即泛函的定义域，通常包含要求 \(y(x)\) 满足一定的边界条件，并且有连续的二阶导数。这样的 \(y(x)\) 称为可取函数。

最简泛函

泛函的形式可以是多种多样的，但是，这里只讨论以下这种积分的形式：

\[\boldsymbol{J}[y] = \int^{x_1}_{x_0} F(x, y, y') dx \]

其中，\(F\) 是它的宗量的已知函数，具有连续的二阶偏导数。称之为 最简泛函 。

最速降线问题

如图所示，在重力的作用下，一个质点从 \((x_0, y_0)\) 处沿着平面曲线 \(y(x)\) 无摩擦地自由下滑到 \((x_1, y_1)\) 点处，则需要的时间为多少？

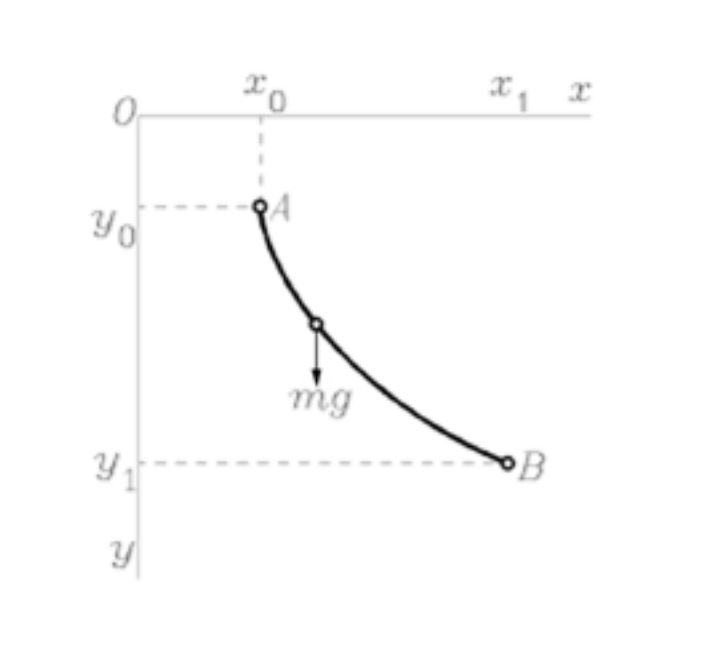
解析：对于微小弧长 \(\Delta S\)，此时速度为 \(v_t\)。则划过微小弧长 \(\Delta S\) 的时长为 \(\Delta t = \frac{\Delta S}{v_t}\)。

由于重力势能转化为动能，则在 \(t\) 时刻质点下降高度 \(h = y_0 - y\) 时，动能为 \(\frac{1}{2} m v_t^2 = m g h\)，则有 \(v_t = 2 g h\)。

那么，\(\Delta t = \frac{\Delta S}{\sqrt{2 g (y_0 - y)}}\)

积分得到，所需时间为：

\[T = \int^{(x_1, y_1)}_{(x_0, y_0)} \frac{ds}{\sqrt{2g(y_0 - y)}} = \int^{x_1}_{x_0} \frac{\sqrt{1 - y'^2}}{\sqrt{2g(y_0 - y)}} dx \]

在这里，要求变量函数 \(y(x)\) 一定通过端点 \((x_0, y_0)\) 和 \((x_1, y_1)\)。