CAP理论
在理论计算机科学中，CAP定理（CAP theorem），又被称作布鲁尔定理（Brewer's theorem），它指出对于一个分布式计算系统来说，不可能同时满足以下三点：[1][2]
- 一致性（Consistency） （等同于所有节点访问同一份最新的数据副本）
- 可用性（Availability）（每次请求都能获取到非错的响应——但是不保证获取的数据为最新数据）
- 分区容错性（Partition tolerance）（以实际效果而言，分区相当于对通信的时限要求。系统如果不能在时限内达成数据一致性，就意味着发生了分区的情况，必须就当前操作在C和A之间做出选择[3]。）
| 术语 | 概念 | 举例 | |
|---|---|---|---|
| C | 一致性 (Consistency) | All nodes see the same data at the same time：所有的节点在同一个时间看到数据是一样的。即一个节点更新了一份数据之后，立即访问其他所有节点所得到的也是最新的数据，如果写失败了，读也失败 | |
| A | 可用性 (Availability) | Reads and writes always get succeed：读和写在任何时候都一样要成功。即所有的请求都有响应，且不会出响应超时或响应错误。 | |
| P | 分区容错性 (Partition tolerance) | The system continues to operate despite arbitrary message loss or failure of part of the system：尽管一个系统出现了数据的丢失或者故障，整个系统仍然能够对外提供正常的一个访问。即分区容错性是分布式系统具备的一个基本的能力，如果一个节点挂掉就不能对外提供，都算不上分布式系统 | MySQL主从，主节点挂掉，从节点还可以顶上来正常提供服务 |
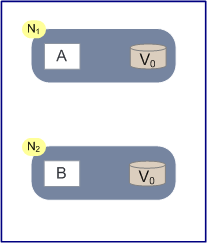
例子：
如上图所示，N1，N2两个节点存储同一份数据V，当前的状态是V0。在节点N1上运行的是安全可靠的写算法A，在节点N2运行的是同样可靠的读算法B，即N1节点负责写操作，N2节点负责读操作。N1节点写入的数据也会自动向N2同步，同步的消息称之为M。如果N1，N2之间出现分区，那么就没法保证消息M在一定的时间内到达N2。
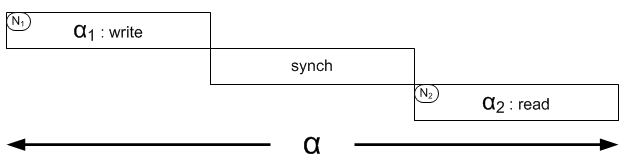
α这个事务由操作α1， α2组成，其中α1是写数据，α2是读数据。如果是单点，那么很容易保证α2能读到α1写入的数据。如果是分布式的情况，除非能控制 α2的发生时间，否则无法保证 α2能读到 α1写入的数据，但任何的控制（比如阻塞，数据集中化等）要么破坏了分区容错性，要么损失了可用性。
synch time :
- 0 : 没有延迟, 保证了一致性。
- N : 不可能没有延迟，保证可用性就无法保证一致性。
