6.3 基于二分搜索树、链表的实现的集合Set复杂度分析
两种集合类的复杂度分析
在【6.1】节与【6.2】节中分别以二分搜索树和链表作为底层实现了集合Set,在本节就两种集合类的复杂度分析进行分析:
测试内容:6.1节与6.2节中使用的书籍。
测试方法:测试两种集合类查找单词所用的时间
//创建一个测试方法 Set<String> set:他们可以是实现了该接口的LinkedListSet和BSTSet对象 private static double testSet(Set<String> set, String filename) { //计算开始时间 long startTime = System.nanoTime(); System.out.println("Pride and Prejudice"); //新建一个ArrayList存放单词 ArrayList<String> words1 = new ArrayList<>(); //通过这个方法将书中所以单词存入word1中 FileOperation.readFile(filename, words1); System.out.println("Total words : " + words1.size()); //增强for循环,定一个字符串word去遍历words //底层的话会把ArrayList words1中的值一个一个的赋值给word for (String word : words1) set.add(word);//不添加重复元素 System.out.println("Total different words : " + set.getSize()); //计算结束时间 long endTime = System.nanoTime(); return (endTime - startTime) / 1000000000.0;//纳秒为单位 } public static void main(String[] args) { //基于二分搜索的集合 BSTSet<String> bstSet = new BSTSet<>(); double time1 = testSet(bstSet, "pride-and-prejudice.txt"); System.out.println("BSTSet:" + time1 + "s"); System.out.println("————————————————————"); //基于链表实现的集合 LinkedListSet<String> linkedListSet = new LinkedListSet<>(); double time2 = testSet(linkedListSet, "pride-and-prejudice.txt"); System.out.println("linkedListSet:" + time2 + "s"); }
结果:BSTSet的速度比LinkedListed的速度快

集合的时间复杂度分析:
1.链表情况
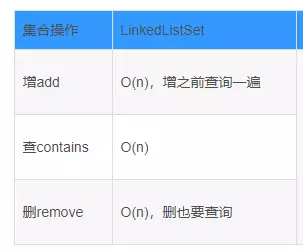
2.二叉搜索树的情况
在基于二叉搜索树的情况下,增加、查询、删除的与二叉搜索树的深度有关,每次操作均为从根节点到某一一支子树的叶子节点之间进行操作,时间复杂度为0(h),h表示二叉搜索树的高度(层数)。
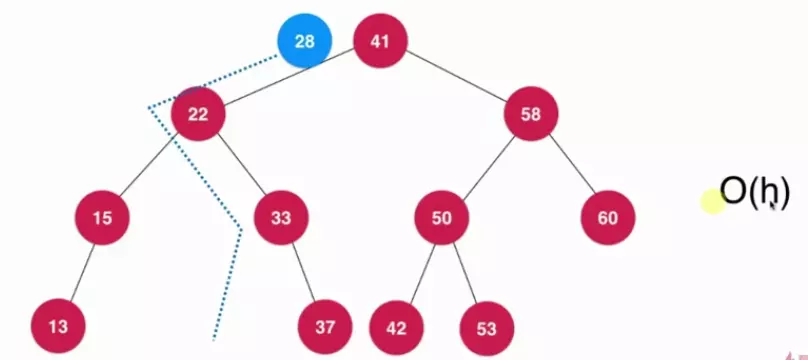
二叉搜索树复杂度如下:
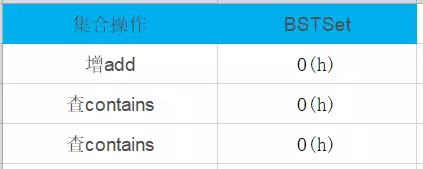
2.1 探究链表情况下的n与二叉搜索树的h的关系
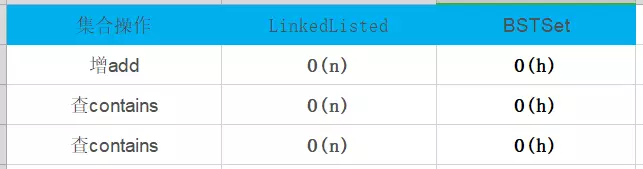
下面对n与h关系进行推导:
2.1.1 采用满二叉树的情况进行分析(最优情况)
采用满二叉树(每个节点都有左右节点,除了叶子节点)来进行分析的原因为满二叉树是一种极端情况,如下图:
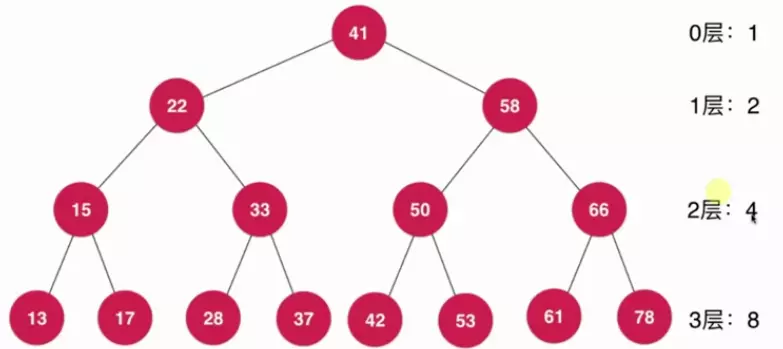
从上图中关于h层总共有多少个节点有如下推导:

假设节点个数为n个则有如下关系:

针对都是log级别的关系,底数是多少不影响它是log级别的则有:
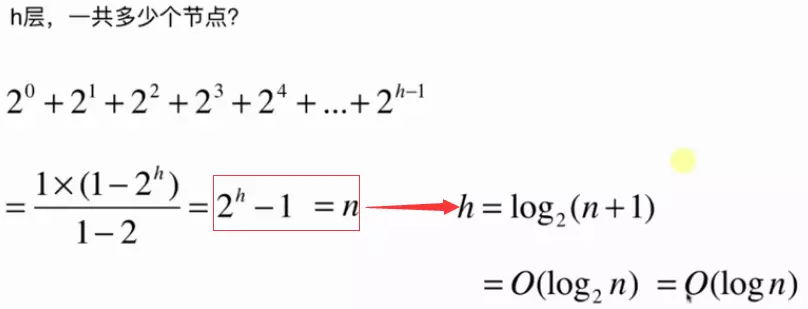
2.1.2 单个孩子情况----二叉搜索树最坏情况(节点数等于其高度)
比如:下面这种二叉搜索树

对于这种只有单个孩子的情况,此时二叉搜索树退化成了链表,此时的时间复杂度为O(n)。
2.2 两种集合复杂度统计

2.2.1 logn和n的差距
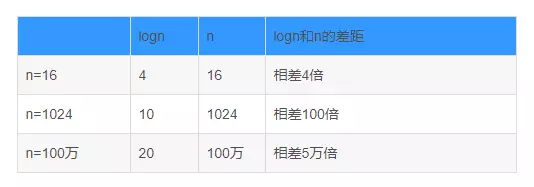
推荐是最好的支持,关注是最大的鼓励。亲爱的朋友,很荣幸在园子里遇到您。
本节涉及的源码地址为 https://github.com/FelixBin/dataStructure/tree/master/src/SetPart
As you wish.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号