4.1递归基础与递归的宏观语意

1.什么是递归

本质上，将原来的问题，转化为更小的同一问题

2.例子分析

假设我们需要对数组进行求和操作（只是为了更好理解递归程序）

要求如下：求解从索引为0到n-1的数组元素和。

分析：

为了能求解从索引为0到n-1的数组元素和，可以分解为第0个数加上索引从1到n-1的数组元素和，如下：

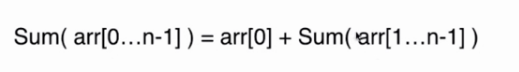
此时求解索引从1到n-1的数组元素和的规模比求解从索引为0到n-1的数组元素和要少一个数以此类推，如下：

.......

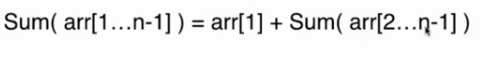
最基本问题：

 3.代码实现本例操作

新建一个package 包名为 Recursion，然后在该包下新建一个SumArray类，相关代码如下

package Recursion;

public class SumArray {
    //调用
    public static int sum(int[] arr) {
        return sum(arr, 0);//0 索引从0开始
    }

    //递归实现数组相加
    //l表示索引

    private static int sum(int[] arr, int l) {
        if (l == arr.length)
            return 0;

        return arr[l] + sum(arr, l + 1);

    }

    //测试
    public static void main(String[] args) {
        int[] nums = {1, 2, 3, 4, 5, 6, 7};
        int value = sum(nums);
        System.out.println(value);
    }
}

结果为：28

对上述代码的分析：

总结：

1、递归函数就是一个函数，完成一个功能，自己调用自己。
2、宏观语意为问题更小的子过程。