2.1基于静态数组---栈的基本实现

1.栈的定义

栈是一种“先进后出”的一种线性数据结构，有压栈出栈两种操作方式。如下图：

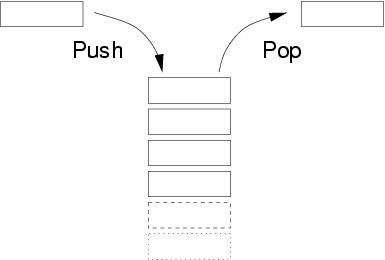
2.栈的分类

栈主要分为两类：

• 静态栈
• 动态栈

【静态栈】

静态栈的核心是数组，类似于一个连续内存的数组，我们只能操作其栈顶元素。

【动态栈】

静态栈的核心是数组，类似于一个连续内存的数组，我们只能操作其栈顶节点。

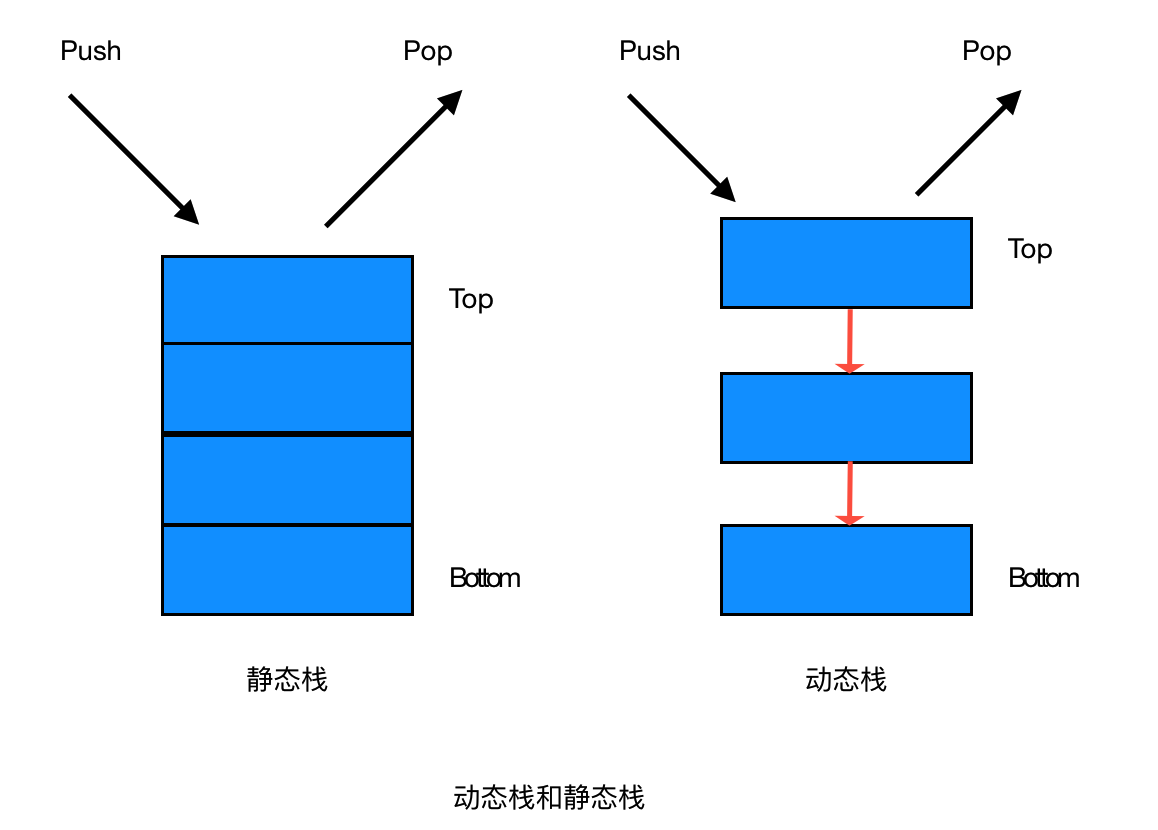
 此节我们在我们之前封装的动态数组的基础上（引用封装好的动态数组），实现基本的栈操作。

3.栈实现

1.先定义一个接口Stack包括相关栈的基本操作

package Stack;

public interface Stack<E> {

    //栈中元素个数
    int getSize();

    //栈中元素个数是否为空
    boolean isEmpty();

    //进栈
    void push(E e);

    //出栈
    E pop();

    //查看栈顶元素
    E peek();
}

2.创建一个ArrayStack类实现接口

package Stack;

import Array.DynamicArray;

public class ArrayStack<E> implements Stack<E> {
    DynamicArray<E> array;

    //构造函数，传入栈的容量capacity构造函数
    public ArrayStack(int capacity) {
        array = new DynamicArray<E>(capacity);
    }

    //无参构造函数，默认栈的容量capacity=10
    public ArrayStack() {
        array = new DynamicArray<E>();
    }

    //获取栈中元素个数
    @Override
    public int getSize() {
        return array.getSize();
    }

    //获取栈中元素数据是否为空
    @Override
    public boolean isEmpty() {
        return array.isEmpty();
    }

    //获取栈的容量
    public int getCapacity() {
        return array.getCapacity();
    }

    //进栈操作
    @Override
    public void push(E e) {
        array.addLast(e);
    }

    //出栈操作
    @Override
    public E pop() {
        return array.removeLast();
    }

    //查看栈顶元素
    @Override
    public E peek() {
        return array.getLast();
    }

    //重写object类的toString方法
    @Override
    public String toString() {
        StringBuilder res = new StringBuilder();
        res.append("Stack:");
        res.append('[');
        for (int i = 0; i < array.getSize(); i++) {
            res.append(array.get(i));
            if (i != array.getSize() - 1) {
                res.append(",");
            }
        }
        res.append("] top");//体现右侧为栈顶
        return res.toString();
    }

}

 

3.测试栈操作是否正确

新建一个类，包含main函数

（1）进栈操作

package Stack;

public class TestMain {
    public static void main(String[] args) {
        ArrayStack<Integer> stack = new ArrayStack<Integer>();
        for (int i = 0; i < 5; i++) {
            stack.push(i);
            System.out.println(stack);
        }
      
    }

}

结果为：

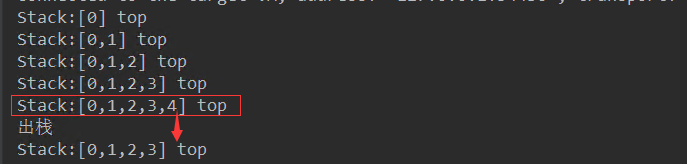
（2）出栈操作

 System.out.println("出栈");
 stack.pop();
 System.out.println(stack);

结果为：

4.栈的复杂度分析

有了我们关于动态数组复杂度分析的知识，在加上此处的栈是基于动态数组实现的，复杂度的分析方式是一致的。

 

源码地址 https://github.com/FelixBin/dataStructure/tree/master/out/test/structure/Stack

 

我的博客即将同步至腾讯云+社区，邀请大家一同入驻：https://cloud.tencent.com/developer/support-plan?invite_code=1h4cn9zbb1k0x