基于Simulink的简单微分方程组仿真

　　到目前为止，我的所有仿真都是自己敲代码，一般利用四阶龙格库塔算法、欧拉算法、预估校正算法（分数阶）等对系统进行仿真。最近我看了点Simulink的内容，发现很多情况下直接利用Simulink比敲代码方便得多，但是对于里面很多模块我不了解，现在对最简单的微分方程组进行仿真做点笔记，这里所谓的最简单就是没有时滞，自治系统，不考虑脉冲、间歇、采样等因素，就是单纯的连续自治微分方程组。
　　当然，这一类系统自己写代码或者用MATLAB自带的ode45函数都比较容易实现，但是，为了学习Simulink，我想选择这些简单的系统熟悉一些模块还是比较好的。利用Simulink搭建微分方程组的方法有很多，我个人感觉，利用自带的“Matlab Function”模块是最方便的，只需要将方程输进去，再加个积分器即可，我们考虑如下Rossler方程：

$\begin{array}{l}
\dot x = - y - z\
\dot y = x + ay\
\dot z = b + (x - c)y
\end{array}$
其中，参数$a=b=0.2$，$c=5.7$，初值可都取零，这个系统实现的Simulink框图如下：

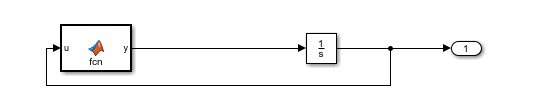
下面说一下每个模块的含义（从左到右）：
1“Matlab Function”模块：将这个模块拖到空白的simulink搭建界面后，双击，即可输入代码，本例中，输入如下代码：

function y = fcn(u)
y=u;
a=0.2;
b=0.2;
c=5.7;
y(1)=-u(2)-u(3);
y(2)=u(1)+a*u(2);
y(3)=b+(u(1)-c)*u(3);

2 积分器模块：作用就是积分一次，将这个模块拖到空白的simulink搭建界面后，双击，在Initial condition框里输入初值，本例[0;0;0]；
3 输出模块：作用就是将运行（积分）完的结果输出到工作空间；
　　这样一来，咱们的Simulink框图搭建就结束了，我想这应该是比写代码方便很多的，下面的问题是，如何调出工作空间的函数。上面的框图按照要求搭建完了之后，我们将它保存在你需要的文件夹里，比如命名为“test2.slxc”，后面的扩展名不用管，可能每个版本略有区别。接下来我们要做的就是新建一个m文件来作图，需要将你新建的m文件和这个搭建的框图放在一个文件夹，这个务必注意，新建的m文件里代码如下：

[t,x]=sim('test2',[0,100]);
plot3(x(:,1),x(:,2),x(:,3));

　　这个代码应该是非常简单的，而且相信大家应该很容易理解，这里简单说明一下。首先，第一行，[t,x]是用来接收返回值的，t接收的是时间变量，x则是咱们刚才保存到空间的系统状态，等号右边的“sim”函数不用咱们管，函数的第一个参数则是咱们刚保存的simulink框图文件，第二个参数“[0,100]”的意思是时间范围，即从0到100，这个可以自由调整。当然，做完图，咱们可以正常的去加一些图例、坐标轴的标题等，这和正常的编程是一样的。咱们运行这里新建的m文件得到下图：

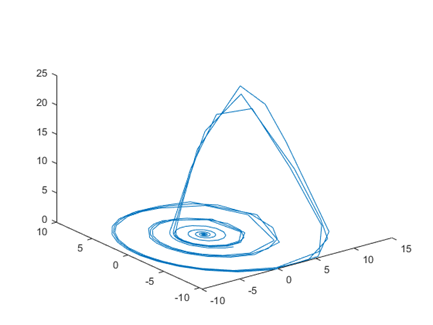
　　大家是否感觉到这里的图很不光滑？这与解方程组的算法有关，默认的算法是变步长的，实际上，咱们是可以调整的，一般来说，我还是建议用咱们之前的四阶龙格库塔方法，固定步长（0.01或者0.001等视具体情况而定）。调整算法和步长的步骤如下：首先在咱们的test2这个simulink的搭建界面的菜单栏上找到“simulation”按钮，点击，下拉框找到“Model Configuration Parameters”按钮，点击，则有如下界面：

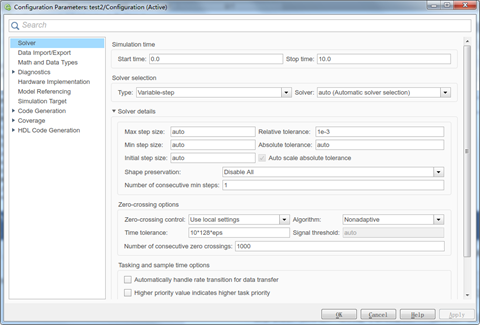
　　看到右边“Solver Selection”选项，点开Type下拉框，选择“Fixed-Step”，选择Solver下拉框，选择“ode4（Runge-Kutta）”，再点开Solver details，设置你需要的固定步长，结果如下图所示，点击OK按钮，然后回到Simulink框图界面，点击保存按钮。

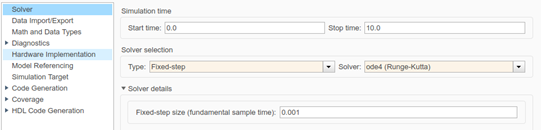
　　之后，再次运行刚才建立的m文件，得到如下结果：

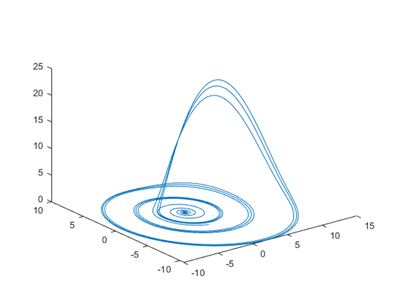
　　不难发现，这次得到的相图很光滑，到此为止，所有的简单微分方程组都可以这样解决了，大家可以自己尝试其它的单个混沌系统仿真。下面我们考虑一下两个系统的同步问题，为了方便起见，我们考虑两个神经网络系统同步，系统的模型如下：
$\begin{array}{l}
\dot x = Ax + Bf(x)\
\dot y = Ay + Bf(y) + u\
u = - D(y - x)
\end{array}$
其中，$f(x) = (|x + 1| - |x - 1|)/2$，$A = - {I_3}$，$D=5{I_3}$，$B = \left[ {\begin{array}{*{20}{c}}
{1.25}&{ - 3.2}&{ - 3.2}\
{ - 3.2}&{1.1}&{ - 4.4}\
{ - 3.2}&{4.4}&1
\end{array}} \right]$，初值：$x(0) = [0.1;0.1;0.1]$，$y(0) = [0.1;0.1;0.100001].$如果不控制，即没有反馈项，尽管两个系统的初值很近，但是随着时间的推移，状态图如下：

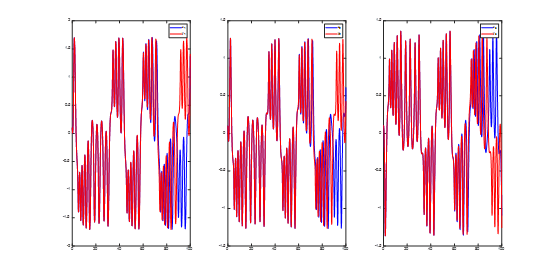
　　这是混沌系统的特性，对初值极为敏感。下面取控制参数如前文所示，得到如下结果：

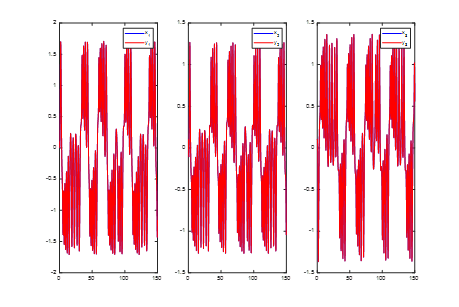
　　在这里处理同步问题时，我们也是将其视为多个微分方程构成的一个大的微分方程组，大家应该能看到，每个程序的区别就是“Matlab Function”模块、积分器中的初值和最后的m文件，这里一共有六个方程，总体思路是将前面三个看成第一个系统，后面三个看成相应系统，由此可得积分器中的初值输入为“[0.1;0.1;0.1;0.1;0.1;0.100001]”， “Matlab Function”模块的代码如下，请大家好好理解一下：

function y = fcn(u)
y=u;
A=-eye(3);D=5*eye(3);
B=[1.25 -3.2 -3.2;-3.2 1.1 -4.4;-3.2 4.4 1];
x1=u(1:3);
y1=u(4:6);
y=[A*x1+0.5*B*(abs(x1+1)-abs(x1-1));A*y1+0.5*B*(abs(y1+1)-abs(y1-1))-D*(y1-x1)];

最后，咱们自己写的m文件代码如下：

[t,xx]=sim('test2',[0,150]);
x=xx(:,1:3);
y=xx(:,4:6);
subplot(1,3,1)
plot(t,x(:,1),'b',t,y(:,1),'r');
legend('x_{1}','y_{1}');
subplot(1,3,2)
plot(t,x(:,2),'b',t,y(:,2),'r');
legend('x_{2}','y_{2}');
subplot(1,3,3)
plot(t,x(:,3),'b',t,y(:,3),'r');
legend('x_{3}','y_{3}');

　　我不对这里的ｍ文件中的代码做任何解释，请大家自行理解。在这里，我们想做驱动系统或者相应系统的相图应该也是轻而易举的。另外，自适应控制方法也可以很容易实现，包括复杂网络的同步等都可以实现。总的来说，只要不含时滞、非自治、脉冲、间歇等的简单微分方程组，利用这个框图都很容易实现，只是“Matlab Function”模块、积分器中的初值和最后的m文件不同。这里省去了复杂的代码，只需要将方程组右端的函数输入即可，麻烦的地方就是最后的m文件，但是，无论用什么方法，都无法省略最后的m文件中的相关语句。简单来说，利用simulink框图可以得到系统各个时刻的状态，最后的m文件就是将这些状态提取出来，作图显示。

2019.10.19 王飞