201871010121-王方 实验二 个人项目—背包问题

项目	内容
课程班级博客链接	2018计算机1班（师范班）
这个作业要求链接	作业要求
我的课程学习目标	1.掌握软件项目个人开发流程 2.掌握Github发布软件项目的操作方法
这个作业在那些方面帮助我实现学习目标	1.这个作业在操作流程方面帮助我掌握软件项目开发流程 2.在整体的操作过程中有利于我总结之前的学习知识
项目Github的仓库链接地址	Github链接

• 一、实验目的与要求
  • (1)掌握软件项目个人开发流程
  • (2)掌握Github发布软件项目的操作方法
• 二、实验内容与步骤

  • 任务1:阅读老师的博客"常用源代码管理工具与开发工具"内容要求，点评班级博客中已提交相关至少3份作业。（已完成）

    • 评论链接1
    • 评论链接2
    • 评论链接3

  • 任务2:详细阅读《构建之法》第1章、第2章，掌握PSP流程。

    • 通过阅读《构建之法》第1章、第2章可以知道第一章讲的是概论，主要讲了软件开发的不同阶段：玩具阶段、业余爱好阶段、探索阶段、成熟的产业阶段；软件工程的定义是：把系统的、有序的、可量化的方法应用到软件的开发、运营和维护上的过程；软件的特殊性：复杂性、不可见性、易变性、服从性、非连续性。计算基础、数学基础、工程基础是软件工程的三大类基础知识领域；Bug的多少可以直接衡量一个软件的开发效率、用户满意度、可靠性和可维护性。所以我们应当思考怎样有效地消灭软件中的Bug？我了解到软件工程真正的样子是软件=程序+软件工程。软件工程不仅仅是简单的软件开发的过程， 而是包括软件开发软件的整个生命周期，都要用到软件工程的东西；更深层次的了解了软件工程的模样，第一章主要是带我们走进了软件工程的世界。
      第二章主要讲了单元测试、回归测试、效能分析、个人软件开发流程。介绍了VSTS写单元测试和回归测试，好的单元测试对一个好的软件起着重要的作用。单元测试要由最熟悉代码的人来写，即程序的作者来写；单元测试要快才能保证效率；单元测试应该产生可重复、一致的结果；单元测试应该覆盖所有代码路径；单元测试应该集成到自动测试的框架中。这一章讲述了一个好的软件工程师应该怎样合理分析软件错误并明确各个模块功能和提高效能还有如何管理自己的源代码。并且这一章还给了我们锻炼编程基本功的方法和如何实践的过程。
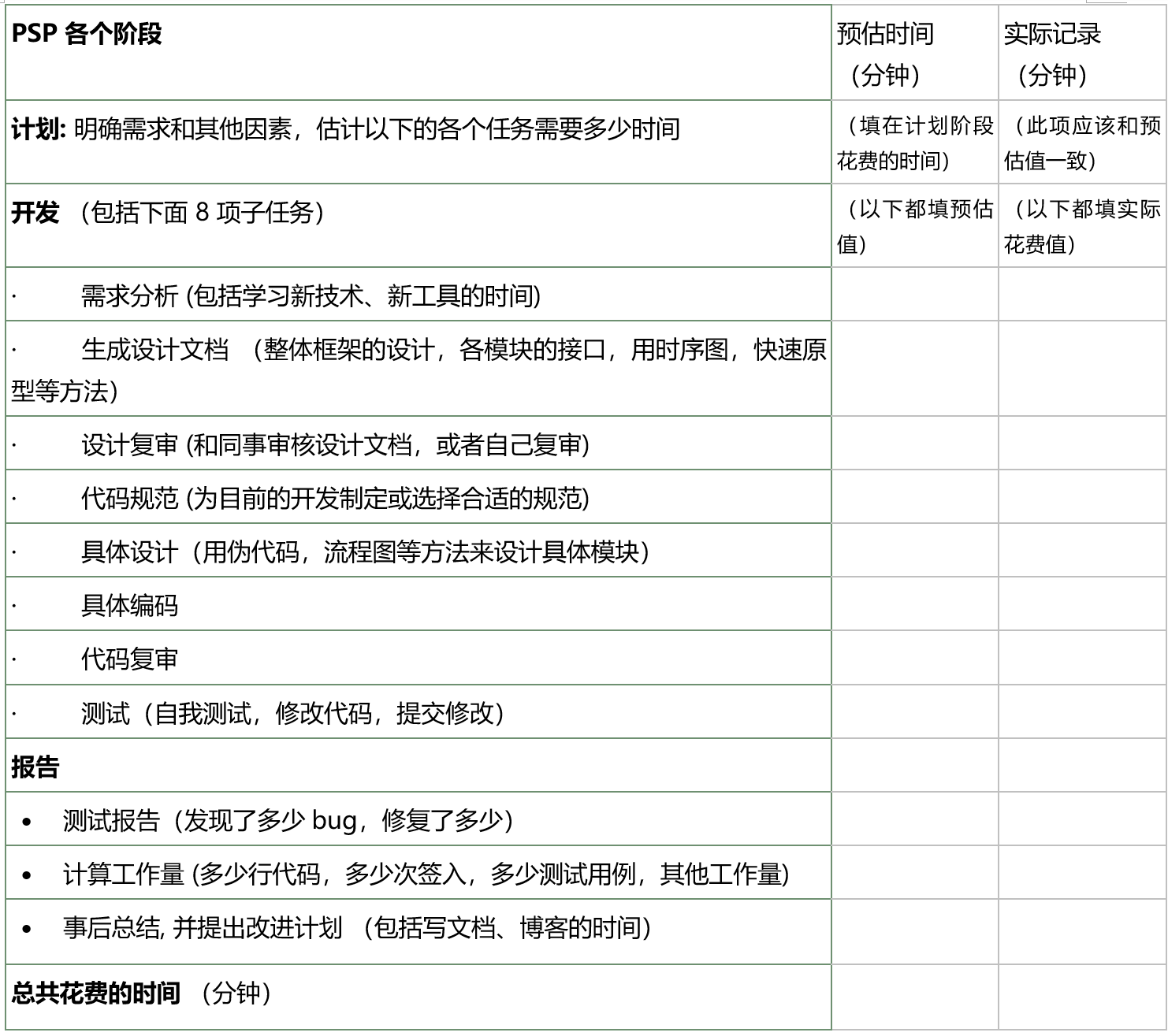
      -PSP流程
      

    • PSP 的特点:

      • 它不局限于某一种软件技术 (如编程语言),而是着眼于软件开发的流程,这样不同应用的工程师可以互相比较。
      • 不依赖于考试,而主要靠工程师自己收集数据,然后统计提高。
      • 在小型初创的团队中，高质量的项目需求很难找到，这意味着给程序员的输入质量不高，在这种情况下,程序员的输出 (程序/软件) 往往质量不高,然而这并不能全部由程序员负责。
      • PSP依赖于数据。
      • 需要工程师输入数据, 记录工程师的各项活动, 这本身就需要不小的代价。
      • PSP的目的是记录工程师如何实现需求的效率,而不是记录顾客对产品的满意度。

  • 任务3:项目开发背景：背包问题（Knapsack Problem，KP）是NP Complete问题，也是一个经典的组合优化问题，有着广泛而重要的应用背景。{０-1}背包问题（{0-1 }Knapsack Problem，{0-1}KP）是最基本的KP问题形式，它的一般描述为：从若干具有价值系数与重量系数的物品（或项）中，选择若干个装入一个具有载重限制的背包，如何选择才能使装入物品的重量系数之和在不超过背包载重前提下价值系数之和达到最大？
    D{0-1} KP 是经典{ 0-1}背包问题的一个拓展形式，用以对实际商业活动中折扣销售、捆绑销售等现象进行最优化求解，达到获利最大化。D{0-1}KP数据集由一组项集组成，每个项集有3项物品可供背包装入选择，其中第三项价值是前两项之和，第三项的重量小于其 他两项之和，算法求解过程中，如果选择了某个项集，则需要确定选择项集的哪个物品，每个项集的三个项中至多有一个可以被选择装入背包，D{0-1} KP问题要求计算在不超过背包载重量 的条件下，从给定的一组项集中选择满足要求装入背包的项，使得装入背包所有项的价值系数之和达到最大；D{0-1}KP instances数据集是研究D{0-1}背包问题时，用于评测和观察设计算法性能的标准数据集；动态规划算法、回溯算法是求解D{0-1}背包问题的经典算法。查阅相关资料，设计一个采用动态规划算法、回溯算法求解D{0-1}背包问题的程序，程序基本功能要求如下：

    • 1.可正确读入实验数据文件的有效D{0-1}KP数据；
    • 2.能够绘制任意一组D{0-1}KP数据以重量为横轴、价值为纵轴的数据散点图；
    • 3.能够对一组D{0-1}KP数据按项集第三项的价值:重量比进行非递增排序；
    • 4.用户能够自主选择动态规划算法、回溯算法求解指定D{0-1} KP数据的最优解和求解时间（以秒为单位）；
    • 5.任意一组D{0-1} KP数据的最优解、求解时间和解向量可保存为txt文件或导出EXCEL文件。

  • 算法分析：　　
    　　回溯算法也叫试探法，通俗的将就是一个方向的路一直往前走，能走则走，不能走则退回来换一个方向再试。一般的实现步骤是：针对一个问题定义解的空间，至少包含问题的一个最优解；用易于搜索的解空间结构，使得能用回溯方法搜索整个解空间；以深度优先的方式搜索整个解空间，并在搜索过程中通过剪枝函数避免无效搜索。
    　　上述问题包含两种情况，一种是将物品放入背包中，另一种是不将物品放入背包中。其中隐含着三个限制条件。第一个限制条件为放入物品的总和不能超过背包的总承重，即当放入的物品总和超过背包的总承重时，即使背包中物品的总价值再大也毫无意义。第二个限制条件为要保证背包中物品的总价值最大。无论第一个条件成不成立，第二个条件总是在其之上的一种更优的选择。第三个限制条件为当达到物品的数量上限，即没有可以获取物品再放入背包时，前两个限制条件均毫无意义，因此需要优先进行判断。这里我们可以将第一种情况看做左节点，第二种情况看做右节点，第三个限制条件用于终结节点的搜索。因此在解决该问题时，首先需要判断是否有物品可以放到背包中，要是没有物品可以放到背包中，直接返回结果，当前的价值即为背包的最优价值。然后判断左节点是否为可行节点，当左节点可行，就优先搜索左子树，不满足则进入右子树。当达到物品的数量上限，直接返回当前物品数量的结果；若左右节点同时不可行，则直接将结果返回上一步。以此类推，将结果从下至上一层一层进行返回，得到问题的最优结果。创建一个物品对象，分别存在价值、重量以及单位重量价值三种属性。

public class Knapsack implements Comparable {
/** 物品重量 /
private int weight;
/* 物品价值 /
private int value;
/* 单位重量价值 */
private int unitValue;

public Knapsack(int weight, int value) {
    this.weight = weight;
    this.value = value;
    this.unitValue = (weight == 0) ? 0 : value / weight;
}

public int getWeight() {
    return weight;
}

public void setWeight(int weight) {
    this.weight = weight;
}

public int getValue() {
    return value;
}

public void setValue(int value) {
    this.value = value;
}

public int getUnitValue() {
    return unitValue;
}

@Override
public int compareTo(Knapsack snapsack) {
    int value = snapsack.unitValue;
    if (unitValue > value)
        return 1;
    if (unitValue < value)
        return -1;
    return 0;
}

按照回溯算法将物品放入背包中：

public class HSSFProblem {
// 待选择的物品
private Knapsack[] bags;
// 背包的总承重
private int totalWeight;
// 背包的当前承重
private int currWeight;
// 待选择物品数量
private int n;
// 放入物品后背包的最优价值
private int bestValue;
// 放入物品和背包的当前价值
private int currValue;

public HSSFProblem(Knapsack[] bags, int totalWeight) {
    this.bags = bags;
    this.totalWeight = totalWeight;
    this.n = bags.length;

    // 物品依据单位重量价值从大到小进行排序
    Arrays.sort(bags, Collections.reverseOrder());
}

public int solve(int i) {

    // 当没有物品可以放入背包时，当前价值为最优价值
    if (i >= n) {
        bestValue = currValue;
        return bestValue;
    }

    // 首要条件：放入当前物品，判断物品放入背包后是否小于背包的总承重
    if (currWeight + bags[i].getWeight() <= totalWeight) {
        // 将物品放入背包中的状态
        currWeight += bags[i].getWeight();
        currValue += bags[i].getValue();

        // 选择下一个物品进行判断
        bestValue = solve(i + 1);

        // 将物品从背包中取出的状态
        currWeight -= bags[i].getWeight();
        currValue -= bags[i].getValue();
    }

    // 次要条件：不放入当前物品，放入下一个物品可能会产生更优的价值，则对下一个物品进行判断
    // 当前价值+剩余价值<=最优价值，不需考虑右子树情况，由于最优价值的结果是由小往上逐层返回，
    // 为了防止错误的将单位重量价值大的物品错误的剔除，需要将物品按照单位重量价值从大到小进行排序
    if (currValue + getSurplusValue(i + 1) > bestValue) {
        // 选择下一个物品进行判断
        bestValue = solve(i + 1);
    }
    return bestValue;
}

// 获得物品的剩余总价值
public int getSurplusValue(int i) {
    int surplusValue = 0;
    for (int j = i; j < n; j++)
        surplusValue += bags[i].getValue();
    return surplusValue;
}

• 任务4：完成任务3的程序开发，将项目源码的完整工程文件提交到你注册Github账号的项目仓库中。

• 展示自己的PSP

PSP 各个阶段	自己预估的时间（分钟）	实际的记录（分钟）
计划:	60	60
开发 :	1500	2880
（1）需求分析	90	150
（2）生成设计文档	60	60
（3）设计复审	0	0
（4）代码规范	30	60
（5）具体设计	720	600
（6）具体编码	500	720
（7）代码复审	50	60
（8）测试	60	90
报告：	90	90
（1）测试报告	60	60
（2）计算工作量	30	30
总结并改进	30	60