树状数组及其实现

树状数组及其实现

引言

树状数组也是一种通过数组来表示树的结构，我们所熟悉的堆与完全二叉树通常也会使用这种方式实现，即，使用数组来表示树。至于完全二叉树(堆是一种特殊的完全二叉树)，树中元素之间的关系较为简单，主要是父节点与子节点之间的关系，这种关系在数组中我们可以通过下标来实现。例如，如果用数组表示一棵完全二叉树的时候，(下标从 1 开始)，对于下标为 \(i\) 的节点，左孩子节点为 \(2i\) 右孩子为 \(2i+1\) 。那么我们可以得出结论，完全二叉树的数组是用数组下标来表示节点之间的父子关系，树状数组不仅能够使用下标表示节点之间的父子关系，还可以表示一些节点(我们称之为区间) 之间的关系。

什么是树状数组

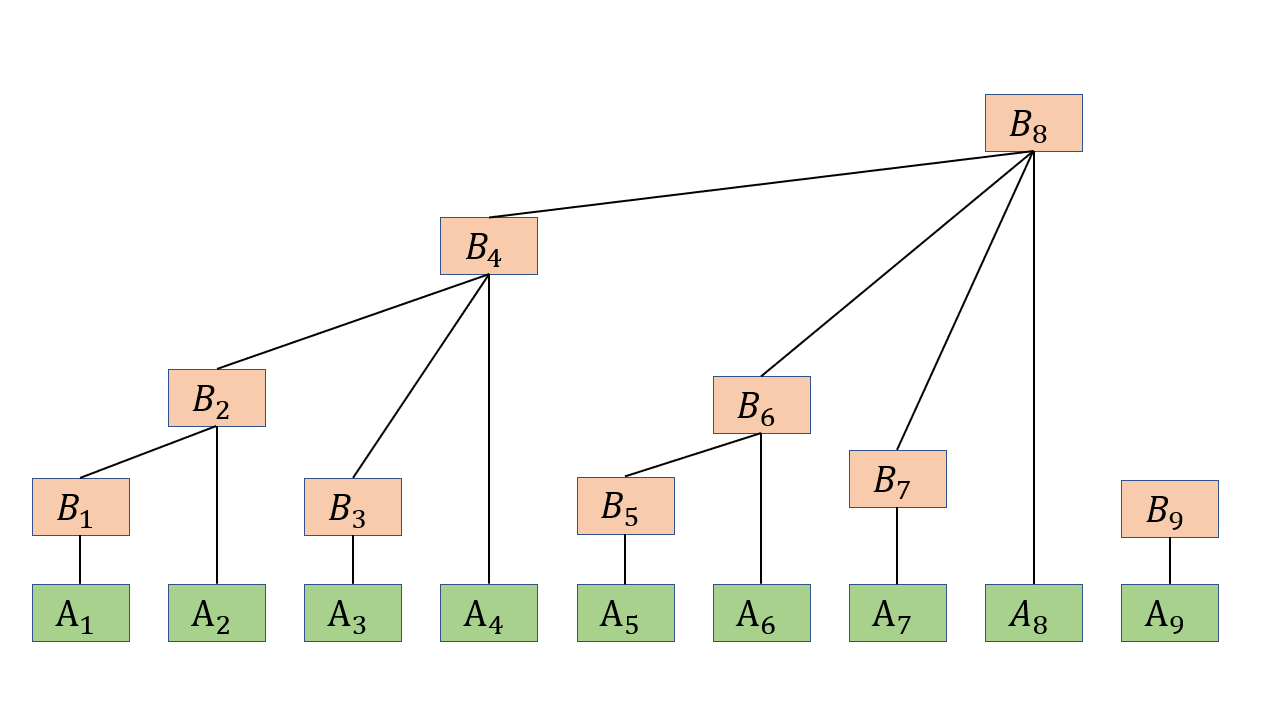
与完全二叉树不同的是，完全二叉树我们的目的是将树映射到数组上，使用数组的下标来表示树中节点间的关系。个人觉得树的结构，本质是探究节点的关系，节点是关键，那么数组最重要的就是下标了。树状数组我个人的理解就是，对于原始数组 \(A\) 中不易实现的下标之间的关系，我们可以将数组进行一次变换，得到一个新的数组 \(B\)，这个新的数组有一些特性，使用这个新数组 \(B\) 的下标可以很好的解决原数组 \(A\) 的问题。这句话听起来很拗口，而且不好理解，只是一句总结性质的话。

所以我们给出一个简单的例子，来说明上面这段话，对于原数组 \(A\)，我们构建一个新数组 \(Sum\) , 其中 \(Sum[i] = \sum_{k=0}^{i}A[k]\) , 这个\(Sum\) 就是一个新数组，它可以很好地解决原数组 \(A\) 上的区间和问题，例如 \(\sum_{k=i}^{j}A[k] = Sum[j]-Sum[i-1]\) , 这就是将数组进行变换解决问题的一种方式，好吧，说了这么多，感觉都是废话。我们回过头来说树状数组吧。

节点的含义与节点之间的关系

对于上面例子中的\(Sum\)​ 数组，节点的含义与节点的关系很清楚，这里就不说了。上图中的树状数组 \(B\)​，它表示的是区间和， 并且，这个区间的大小是 \(2^k (k\geq 0)\)​ , 因此，我们很容易想到，对于任何一个区间大小我可以表示为 \(S = 2^{k_1} + 2^{k_2}+...+2^{k_n}\)​ 。对于\(B\) 的含义，\(B_4\) 表示的是 \(A_1\) 到 \(A_4\) 的区间和。\(B_6\) 表示的是 \(A_5\) 到 \(A_6\) 的区间和。那么对于 \(B\) 数组中的一个节点，它表示的区间大小是多少呢，例如 \(B_4\) 区间大小是 4，\(B_6\) 区间大小是 2。回答这个问题之前，我们先要弄明白 \(B\) 数组的节点(本质是数组下标) 之间的关系。

节点之间的关系

\(B\) 数组节点之间的关系要从构建数组的时候说起，从 \(A\) 数组构建一个 \(B\) 数组的方式是从下往上，也就是说从叶子节点向根节点构建。构建的方式(下标之间的关系是)：对于 \(A\) 数组中的奇数节点，\(B[i] = A[i]\) , 对于偶数节点，首先, \(A[i]\) 就是 \(B[i]\) 的一个子节点, 从子节点 \(B[i]\) 到父节点的关系是， \(Parent_{B_i} = i + 2^{k}\) , 其中 \(i\) 表示的是下标，其中 \(k\) 是 \(i\) 的 \(lowbit\) ，至于为什么这么构造，大家无需纠结，我也不知道，但是，正是因为这样构造了，\(B\) 数组才有一些良好的性质, 所以我们会使用这种父子关系推导出 \(B\) 数组的一些性质.

性质1 (B所表示的区间大小与B的含义)

\(B\) 数组中, 节点与子节点之间的关系, 我们已经说明了, 我们也可以在图中观察到他们之间的这种关系. \(B\) 节点表示的是区间和, 对于这个区间和, 我们也从下往上看, 即从子节点到父节点, \(B_i\) 的父节点所表示的区间一定包括 \(B_i\) , 同时也会包括其它的子节点, \(B_k\) . 因此, 节点 \(B_j\) 所表示的区间, 是它所有子节点的区间的并集以及 \(A_i\) . 这一点, 我们在图中也可以看到, 用公式表示就是:

\[\begin{aligned} B_{1} &= A_{1} \\ B_{2} &= B_{1} + A_{2} = A_{1} + A_{2} \\ B_{3} &= A_{3} \\ B_{4} &= B_{2} + B_{3} + A_{4} = A_{1} + A_{2} + A_{3} + A_{4} \\ B_{5} &= A_{5} \\ B_{6} &= B_{5} + A_{6} = A_{5} + A_{6} \\ B_{7} &= A_{7} \\ B_{8} &= B_{4} + B_{6} + B_{7} + A_{8} = A_{1} + A_{2} + A_{3} + A_{4} + A_{5} + A_{6} + A_{7} + A_{8} \\ \end{aligned} \]

因此, 我们可以通过数学归纳法得出 \(B\) 区间的大小为 \(2^k - 1\) .

\[B_{i} = \sum_{j = i - (2^{k} - 1)}^{i} A_{j} \]

其中 \(k\) 是 \(i\) 的 \(lowbit\) , 这里使用的是归纳法, 并没有一个直观的推导过程.

性质 2 (lowbit)

lowbit 的含义是 \(i\) 的二进制中从最低位到高位连续零的长度, 对于 \(lowbit(i)\) 的计算方式, 参考负数的存储方式, 负数是以补码存储的，对于整数运算 \(x\&(-x)\) 有我们可以得到:

1. 当 \(x\) 为0时，即 $0 & 0 $，结果为 0
2. 当 \(x\) 为奇数时，最后一个比特位为1，取反加1没有进位，故\(x\)和 \(-x\) 除最后一位外前面的位正好相反，按位与结果为0, 结果为1.
3. 当 \(x\) 为偶数，若 \(x = 2^m\)，\(x\) 的二进制表示中只有一位是1（从右往左的第\(m+1\)位, 最高位），其右边有\(m\)位 0，故 \(x\) 取反加1后，从右到左第有m个0，第 \(m+1\) 位及其左边全是1。这样，\(x\& (-x)\) 得到的就是\(x\) .
4. 当\(x\)为偶数，并且 \(x != 2^m\)，可以写作 \(x= y * (2^k)\) .其中，\(y\) 的最低位为1。实际上就是把 \(x\) 用一个奇数左移 \(k\) 位来表示。这时，\(x\) 的二进制表示最右边有\(k\)个0，从右往左第 \(k+1\) 位为1。当对 \(x\) 取反时，最右边的 \(k\) 位 \(0\) 变成1，第 \(k+1\) 位变为0；再加1，最右边的\(k\) 位就又变成了0，第 \(k+1\) 位因为进位的关系变成了1。左边的位因为没有进位，正好和 \(x\) 原来对应的位上的值相反。二者按位与，得到：第\(k+1\) 位上为1，左边右边都为0。结果为 \(2^k\).

int lowbit(int x){
    return x&(-x);
}

树状数组的操作

节点更新

更新节点的时候, 首先是更新了数组 \(A\), 我们怎样将 \(A\) 数组的更新映射到 \(B\) 数组中呢, 首先, 在图中, 我们将 \(B[i]\) 作为 \(A[i]\) 的父节点, 然后 \(B[i]\) 的父节点所表示的区间包含 \(B[i]\) 所表示的区间, 所以我们要将 \(B\) 数组中叶子节点 \(B[i]\) 到根节点路径上的所有节点的值更新, 因为这些节点所表示的区间都包括 \(A[i]\). 请注意， 如下代码中的 \(k\) 是 \(A\) 数组的增量, 而不是 \(B\) 数组的增量.

void update_data(int i,int k){    //在i位置加上k
    while(i <= n){
        B[i] += k;
        i += lowbit(i); // B[i] 的父节点
    }
}

区间查询

这里区间查询表示的是, 静态情况的查询, 或者改变区间中一个点的值, 然后查询. 例如,区间求和问题, \(Sum[i:j] = Sum[j] - Sum[i-1]\) , 我们可以结合上述的节点更新, 在更新直接查询区间, 要求得 \(Sum[i:j]\) 只需要知道 \(Sum[i]\) 的计算方式就可以了.

\[\begin{aligned} Sum(i) &= A_{1} + A_{2} + ...... + A_{i} \\ &= A_{1} + A_{2} + A_{i-2^{k}} + A_{i-2^{k}+1} + ...... + A_{i} \\ &= A_{1} + A_{2} + A_{i-2^{k}} + B_{i} \\ &= Sum(i-2^{k}) + B_{i} \\ &= Sum(i-lowbit(i)) + B_{i} \\ \end{aligned} \]

所以, 计算 \(Sum[i]\) 是一个递归的过程. 当然, 我么也可以使用 while 循环来实现:

int getsum(int i){        //求Sum[i], 注意 A[] 和 B[] 下标是从 1 开始的
    int res = 0;
    while(i > 0){
        res += B[i];
        i -= lowbit(i);  // Sum[i - lowbit[i]]
    }
    return res;
}

树状数组的功能

区间增减 + 单点查询

这就是第一个问题，如果题目是让你把 \(A[x:y]\) 区间内的所有值全部加上 \(k\) 或者减去 \(k\)，然后查询操作是问某个点的值，这种时候该怎么做呢。如果是像上面的树状数组来说，就必须把 \(A[x:y]\)区间内每个值都更新，这样的复杂度肯定是不行的，这个时候，就不能再用数据的值建树了，这里我们引入差分，利用差分建树. 定义差分数组 \(C_i = A_i - A_{i-1}\) , 那么有:

\[\begin{aligned} C_{1} &= A_{1} - 0\\ C_{2} &= A_{2} - A_{1}\\ ......\\ C_{n} &= A_{n} - A_{n-1}\\ \sum_{j=1}^{n}C_{j} &= A_{n}\\ \end{aligned} \]

区间增减：在 \([x,y]\) 区间内每一个数都增加 \(v\)，只影响 2 个单点的值:

\[\begin{aligned} C_{x} &= (A_{x} + v) - A_{x-1}\\ C_{x+1} &= (A_{x+1} + v) - (A_{x} + v)\\ C_{x+2} &= (A_{x+2} + v) - (A_{x+1} + v)\\ ......\\ C_{y} &= (A_{y} + v) - (A_{y-1} + v)\\ C_{y+1} &= A_{y+1} - (A_{y} + v)\\ \end{aligned} \]

我们发现, 只有 \(C_x\) 和 \(C_{y+1}\) 的值改变了, 所以我们可以只用 update_data 函数更新这两个点的值, 然后对于查询 \(A_i\) 使用 GetSum(i) 函数即可.

区间增减 + 区间查询

因为要在区间上对数据进行更新, 我们依然构造差分数组, 这里主要说明区间查询怎么做。先来看 \([1,n]\) 区间和如何求：

\[A_{1} + A_{2} + A_{3} + ...... + A_{n}\\ \begin{aligned} &= (C_{1}) + (C_{1} + C_{2}) + (C_{1} + C_{2} + C_{3}) + ...... + \sum_{i=1}^{n}C_{i}\\ &= n * C_{1} + (n-1) * C_{2} + ...... + C_{n}\\ &= n * (C_{1} + C_{2} + C_{3} + ...... + C_{n}) - (0 * C_{1} + 1 * C_{2} + 2 * C_{3} + ...... + (n - 1) * C_{n})\\ &= n * \sum_{i=1}^{n}C_{i} - (D_{1} + D_{2} + D_{3} + ...... + D_{n})\\ &= n * \sum_{i=1}^{n}C_{i} - \sum_{j=1}^{n}D_{j}\\ \end{aligned} \]

其中 \(D_n = (n-1)*C_n\) .

所以求区间和，只需要再构造一个 \(D_n\) 即可,

\[\begin{aligned} \sum_{i=1}^{n}A_{i} &= A_{1} + A_{2} + A_{3} + ...... + A_{n} \\ &= n * \sum_{i=1}^{n}C_{i} - \sum_{j=1}^{n}D_{j}\\ \end{aligned} \]

以此类推到一般区间\([x:y]\) :

\[\begin{aligned} \sum_{i=x}^{y}A_{i} &= A_{x} + A_{x+1} + A_{x+2} + ...... + A_{y} \\ &= \sum_{i=1}^{y}A_{i} - \sum_{j=1}^{x-1}A_{j}\\ &= (y * \sum_{i=1}^{y}C_{i} - \sum_{j=1}^{y}D_{j}) - ((x-1) * \sum_{i=1}^{x-1}C_{i-1} - \sum_{j=1}^{x-1}D_{i-1})\\ \end{aligned} \]

具体实现的时候, 我们可以维持两个数组分别表示 \(C\) 和 \(D\).

int lowbit(int x) {
    return x &(-x);
}

void updata_data(int x, int k) {
    int i = x;
    while(i<=n) {
        C[i] += k;
        D[i] += k*(i-1);
        i = i+lowbit(i);
    }
}

int GetSum(int i) {
    int result1 = 0, result2 = 0, n = i;
    while (i>0) {
        result1 += C[i]; 
        result2 += D[i];
        i -= lowbit(i);
    }
    return n*result1 - result2;
}