CS224n学习笔记(一)

How do we have usable meaning in a computer?

Represents the words as discrete symbols, (离散型变量)

Use the one-hot vector to represent the word in sentence, (Traditional way, we can use Distributional semantics)

Distributional semantics: A word's meaning is giving by words that frequently appear close-by.

when a word w appear in a text, its context words is the set of words that appears nearby. We can use many contexts of w to build up a representation of w.

Word Vector:We build a dense(稠密的) vector for each word, chosen so that it's similar to vector of words that appear in similar contexts, it's a probability vector .

所有的句子都表示 banking的意思。

\[bank =\left( \begin{array}{r}{0.286} \\ {0.792} \\ {-0.177} \\ {-0.107} \\ {0.109} \\ {-0.549} \\ {0.371}\end{array}\right) \]

单词向量有时候又叫做word embedding 或者 word representation。上面是分布式 distributed representation。不仅仅是一个简单的位置向量，每一个单词都有一个 distributed representation，就构成了向量空间。

Word2vec是一个框架用于学习单词向量。

主要思想：

• 有一大簇的文本
• 每一个单词在一个确定的词典中可以用向量表示
• Go through文本中的每一个位置，这个文本有一个中心单词 C 以及 context(“outside 单词”) O。我们要观察这个单词周围的单词。
• 使用单词 C与单词 O的单词向量的相似性来计算给定的 O，是C的概率
• 调整这个单词向量，直到最大化这个概率

使用中间的单词可以预测出周围的单词

例如对于下面这个例子来说：

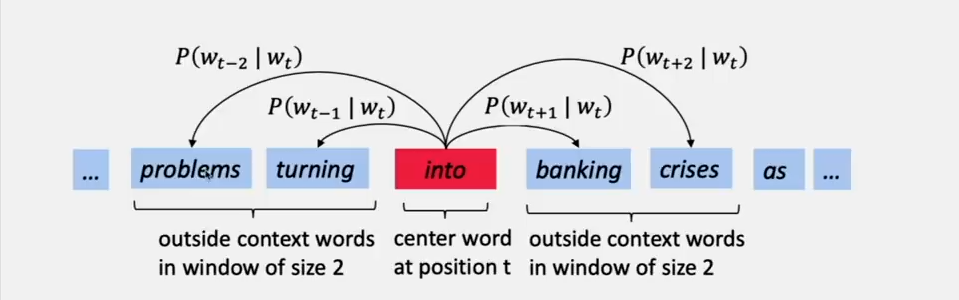
我们需要计算的是 \(P\left(w_{t+j} | w_{t}\right)\)。

我们希望的是通过周围的单词预测出中间的单词 ‘into’ 。所以我们可以改变这些预测，如果我们从贝叶斯的角度看的话，那么就是我们先计算出当遇到 'into' 的时候，周围每个单词的概率作为先验，然后当遇到周围的单词的时候，用后验就可以算出单词是 ‘into’的概率。

对于 Word2vec的目标函数函数

对于文本中的每一个位置，\(t=1, \dots, T\)来说预测用一个确定大小为 m的窗口预测 context words， 对于中心单词 \(w_{j}\)。目标函数就是

\[LikeLihhod =L(\theta)=\prod_{t=1}^{T} \prod_{-m \leq j \leq m \atop j \neq 0} P\left(w_{t+j} | w_{t} ; \theta\right) \]

m 表示窗口的大小，\(L(\theta)\) 是关于最优化 \(\theta\)的函数，那么 \(J(\theta)\)就是 negative log 似然函数。\(\theta\) 恰恰就是单词向量

\[J(\theta)=-\frac{1}{T} \log L(\theta)=-\frac{1}{T} \sum_{t=1}^{T} \sum_{-m \leq j \leq m \atop j \neq 0} \log P\left(w_{t+j} | w_{t} ; \theta\right) \]

上面的 \(J(\theta)\) 是损失函数，也就是目标函数。最小化目标函数等价于最大化预测的准确率。

这个 \(\theta\) is actually going to be the vector representation. Use that word to predict what the other words occur

那么问题来了，怎么计算 P函数。

对于每个word，我们有两种表现方法，分别是：

• \(v_{w}\) when \(w\) is a center word
• \(u_{w}\) when \(w\) is a context word

那么对于中心单词 c 于 context word o来说：

\[P(o | c)=\frac{\exp \left(u_{o}^{T} v_{c}\right)}{\sum_{w \in V} \exp \left(u_{w}^{T} v_{c}\right)} \]

对于前面的例子来说就是：\(P\left(u_{\text {problems}} | v_{i n t o}\right)\) short for \(\mathrm{P}\left(problems|into; u_{\text {problems}}, v_{i n t o}, \theta\right)\)

上面公式的解释，我们使用的是 \(u_{o}^{T} v_{c}\)来表示权重的大小。也就是两个单词间的关联程度，\(u_{o}^{T} v_{c}\)越大越相关，（从向量的角度解释）。分母是所有的情况。然后是一个 \(Softmax\)函数：

\[\operatorname{softmax}\left(x_{i}\right)=\frac{\exp \left(x_{i}\right)}{\sum_{j=1}^{n} \exp \left(x_{j}\right)}=p_{i} \]

这个比较容易理解。这个公式也用于后面的CBOW 以及 skip-gram计算损失函数时候。

梯度下降解最小化损失函数

我们的参数只有一个 \(\theta\)，但是请记住 \(\theta\) 包含中心向量与 context word向量，所以是两截长。这里我们只是用 \(\theta\) 来模糊的表示位置参数，那么 \(\theta\) 到底是一个什么样的参数呢？在 CBOW 与 skip-gram中可以理解为两个矩阵。这个后面再说。所以用梯度下降求解损失函数也放在后面。

\[\theta=\left[ \begin{array}{l}{v_{\text {aardvark}}} \\ {v_{a}} \\ {\vdots} \\ {v_{z e b r a}} \\ {u_{\text {aardvark}}} \\ {u_{a}} \\ {\vdots} \\ {u_{z e b r a}}\end{array}\right] \in \mathbb{R}^{2 d V} \]

基于 SVD的方法获得单词向量

在具体使用word2vec之前，我们先讲一下使用 SVD(奇异值分解)的方法，这个比较简单，但是这个方法十分有用，潜在语义索引(LSI) 就可以使用这种方法。we first loop over(遍历) a massive dataset and accumulate word co-occurrence counts in some form of a matrix X。 然后对 X矩阵使用 SVD（奇异值分解），获得 \(US V^{T}\)。我们使用 U的行向量作为词典中所有单词的单词向量。

Word-Document Matrixs

构造 X的矩阵的方法如下，遍历所有的文件(billions of)，word i 每出现在 文档 j 中一次 ， 那么 \(X_{i j}\)就+ 1. 可以看出 \(\left(\mathbb{R}^{|V| \times M}\right)\)这个矩阵超级大。

Window based Co-occurrence Matrix

这种方法记录的不是单词与文本之间的联系，而是单词于单词之间，共同出现的情况下的联系：

比如说图中的例子：

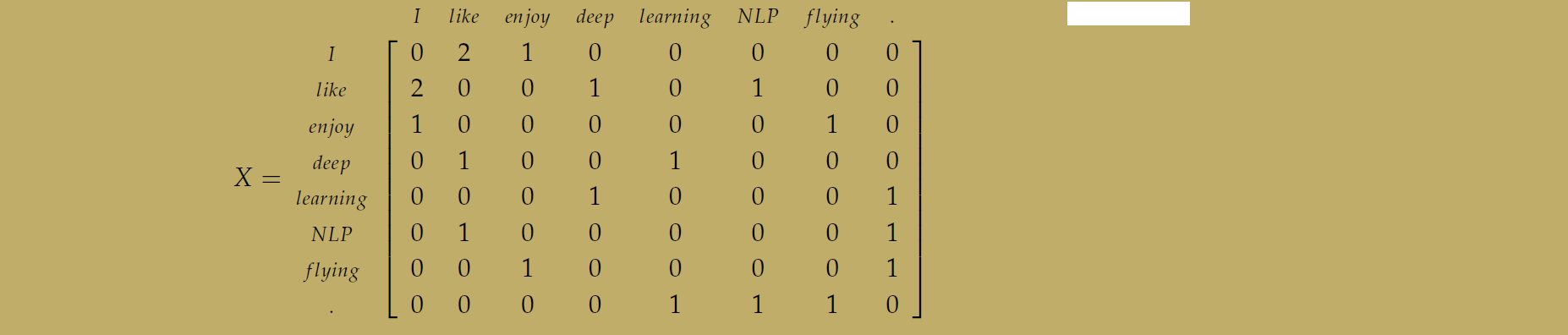
Applying SVD to the cooccurrence matrix

对上面的关系矩阵使用 SVD变换，我们的做法就是提取了前 k个特征向量，用来表示单词向量。

\[\frac{\sum_{i=1}^{k} \sigma_{i}}{\sum_{i=1}^{|V|} \sigma_{i}} \]

下面的图可以看到具体的方法，奇异值分解后得到三个矩阵，对中间的 S矩阵取前 k个对角线的数值。

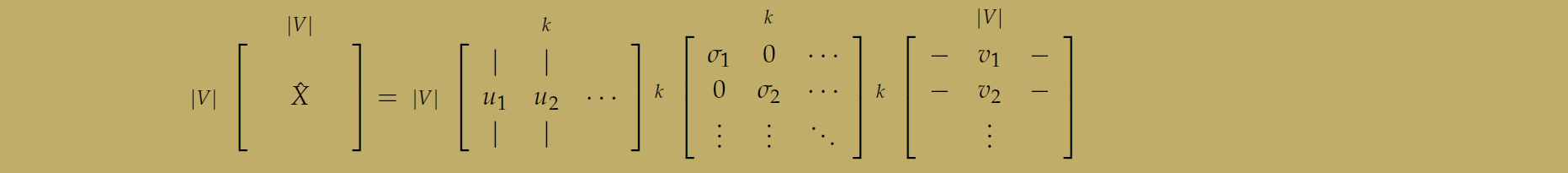
所以前面的 U矩阵的列向量只有 k个，这样就降低了单词向量的维度。这个方法还面临这许多问题。

基于迭代的方法 - Word2vec

两个算法：CBOW 和 skip-gram

两种训练方法：negative sampling and hierarchical softmax

Language Models

首先需要理解，我们是将一个概率赋给一个序列的单词。从数学上表示，\(P\left(w_{1}, w_{2}, \cdots, w_{n}\right)\)。如果我们假设每个单词的出现是完全独立的，那么：

\[P\left(w_{1}, w_{2}, \cdots, w_{n}\right)=\prod_{i=1}^{n} P\left(w_{i}\right) \]

这个假设显然不合理，因为大多数情况下，句子中，单词间有一定的关系，比如说，‘read’ 后面 往往是 ‘book’ 或者是 ‘maganize’ 等。所以我们将这个句子的概率表示成，句子中出现的成对的单词，表示成这个单词与他下一个单词为一对，可以写成这样：

\[P\left(w_{1}, w_{2}, \cdots, w_{n}\right)=\prod_{i=2}^{n} P\left(w_{i} | w_{i-1}\right) \]

以上就是我们表示一个序列的概率的例子。

Continuous Bag of Words Model (CBOW)

通过上下文预测中间单词。

对于词袋模型，我们输入，(上下文的one-hot表示的单词向量)用 \(x^{(c)}\)来表示。输出用 \(y^{(c)}\)来表示，我们训练的时候，输出只有一个 \(y\) 表示中心词。下面定义未知数：

首先定义两个矩阵：

\[\mathcal{V} \in \mathbb{R}^{n \times|V|} \text { and } \mathcal{U} \in \mathbb{R}^{|V| \times n} \]

这里面 n 定义了单词向量空间的大小， \(\mathcal{V}\)是输入矩阵，\(\mathcal{V}\) 的第 i 列是 对于输入单词 \(w_{i}\) 所表示的 n 维向量。我们表示成 \(n \times 1\) 向量 \(v_{i}\)。同理对于输出，\(\mathcal{U}\) 是输出矩阵，输出矩阵 \(\mathcal{U}\) 的第 j 行是一个 n 维的单词向量作为单词 \(w_{i}\) 的输出向量。我们表示成 \(u_{j}\)。 为什么可以这么说呢？从线性代数的角度来说，我们最开始的输入是 one-hot编码的 \(x^{(c)}\)，我们可以理解为矩阵 \(\mathcal{V}\) 对向量 \(x^{(c)}\) 的线性变换。 \(v_{i}\) 完全由参数 \(i\) 与矩阵 \(\mathcal{V}\) 决定，所以我们可以直接当成是输入，这里巧妙的就是，我们最后优化的，也是这个 \(v_{i}\) 。

下面是具体的步骤，

1. 对于输入大小为 m 的上下文， 我们产生一个one-hot 编码为

   \[\left(x^{(c-m)}, \ldots, x^{(c-1)}, x^{(c+1)}, \ldots, x^{(c+m)} \in \mathbb{R}^{|V|}\right) \]

2. 这个上下文的单词向量就是\((v_{c-m}=\mathcal{V} x^{(c-m)}, v_{c-m+1}=\mathcal{V} x^{(c-m+1)}, \ldots, v_{c+m}=\mathcal{V} x^{(c+m)} \in \mathbb{R}^{n} )\)

3. 将这些向量求平均值得到：

   \[\hat{v}=\frac{v_{c-m}+v_{c-m+1}+\ldots+v_{c+m}}{2 m} \in \mathbb{R}^{n} \]

4. 产生一个用来表示分数的向量 \(z=\mathcal{U} \hat{v} \in \mathbb{R}^{|V|}\)，而实际上打分的是矩阵 \(\mathcal{U}\) 。由于相似矢量的点积更高，那么我们最大化点积的话，相似的单词就会靠的越近。

5. 将分数通过 softmax函数：\(\hat{y}=\operatorname{softmax}(z) \in \mathbb{R}^{|V|}\)

6. 我们希望得分最高的是中心词，训练的中心词我们用 \(y \in \mathbb{R}|V|\)表示，而我们预测的结果用 \(\hat{y} \in \mathbb{R}|V|\)来表示。

现在我们要得到矩阵 \(\mathcal{V}\) 和 \(\mathcal{U}\) ，那么我们就要一个目标函数，然后最小化损失函数就可以了。我们使用信息学中的cross-entropy(交叉熵)损失函数，\(H(\hat{y}, y)\)。从离散的角度，我们可以写成下面的公式，\(y\) 向量的每一个位置都要最为离散的偏差算进来。

\[H(\hat{y}, y)=-\sum_{j=1}^{|V|} y_{j} \log \left(\hat{y}_{j}\right) \]

但是 \(y\) 是一个one-hot编码，所以 \(H(\hat{y}, y)=-y_{i} \log \left(\hat{y}_{i}\right)\)。 最理想的情况下 \(\hat{y}_{i}\) = 1，与 \(y_{i}\) 是相同的。但是预测的会有偏差。如果 $\hat{y}_{i} < 1 $那么 \(H(\hat{y}, y)\) > 0。因此最优化，我们写成下式：

\[最小化 J = \]

\[\begin{array}{l}{=-\log P\left(w_{c} | w_{c-m}, \ldots, w_{c-1}, w_{c+1}, \ldots, w_{c+m}\right)} \\ {=-\log P\left(u_{c} | \hat{v}\right)} \\ {=-\log \frac{\exp \left(u_{c}^{T} \hat{v}\right)}{\sum_{j=1}^{|V|} \exp \left(u_{j}^{T} \hat{v}\right)}} \\ {=-u_{c}^{T} \hat{v}+\log \sum_{j=1}^{|V|} \exp \left(u_{j}^{T} \hat{v}\right)}\end{array} \]

然后使用随机梯度下降更新 \(u_{c}\) and \(v_{j}\)。上述式子在理解的过程中，关键的地方是要知道还未经过 \(softmax\) 函数的时候，我们用 \(u_{c}\)来表示 \(w_{c}\)。而输入使用的是 \(\mathcal{V}\) 的列向量表示的，处理之后，用 \(\hat{v}\)来表示。

Skip-Gram Model

该算法与 CBOW的思路相反。是通过中心词预测上下文的单词向量：我们输入用 \(x\) 表示 ，输出用 \(y^{(j)}\) 来表示，我们定义相同的矩阵 \(\mathcal{V}\) 和 \(\mathcal{U}\) 。该算法也分成六部完成：

1. 中心单词的 one-hot编码，用 \(x \in \mathbb{R}^{|V|}\)来表示。
2. 我们产生单词向量 \(v_{c}=V x \in\mathbb{R}^{n}\)。这一步使用了矩阵 \(\mathcal{V}\) 。
3. 然后使用 \(z=\mathcal{U} v_{c}\) 得到，\(z\) 是一个矩阵，用来表示每个预测的 \(y\)。
4. 然后使用 softmax函数，\(\hat{y}=\operatorname{softmax}(z)\)。 然后假设 \(\hat{y}_{c-m}, \dots, \hat{y}_{c-1}, \hat{y}_{c+1}, \dots, \hat{y}_{c+m}\) 是观察到每一个文本向量的概率。
5. 我们希望的是我们产生的概率 \(\hat{y}_{c-m}, \dots, \hat{y}_{c-1}, \hat{y}_{c+1}, \dots, \hat{y}_{c+m}\) 与实际的概率 \(y^{(c-m)}, \ldots, y^{(c-1)}, y^{(c+1)}, \ldots, y^{(c+m)}\)相等。实际的概率就是每一个单词的 one-hot编码。

接下来就是定义目标函数以及最小化损失函数：\(J\) =

\[\begin{aligned} J &=-\sum_{j=0, j \neq m}^{2 m} \log P\left(u_{c-m+j} | v_{c}\right) \\ &=\sum_{j=0, j \neq m}^{2 m} H\left(\hat{y}, y_{c-m+j}\right) \end{aligned} \]

\[\begin{array}{l}{=-\log P\left(w_{c-m}, \ldots, w_{c-1}, w_{c+1}, \ldots, w_{c+m} | w_{c}\right)} \\ {=-\log \prod_{j=0, j \neq m}^{2 m} P\left(w_{c-m+j} | w_{c}\right)} \\ {=-\log \prod_{j=0, j \neq m}^{2 m} P\left(u_{c-m+j} | v_{c}\right)} \\ {=-\log \prod_{j=0, j \neq m}^{2 m} \frac{\exp \left(u_{c-m+j}^{T} v_{c}\right)}{\sum_{k=1}^{|V|} \exp \left(u_{k}^{T} v_{c}\right)}} \\ {=-\log \prod_{j=0, j \neq m}^{2 m} u_{c-m+j}^{T} v_{c}+2 m \log \sum_{k=1}^{|V|} \exp \left(u_{k}^{T} v_{c}\right)}\end{array} \]

上面的损失函数就比较好理解了。

Negative Sampling

前面计算面临的问题，在 \(softmax\) 阶段，计算量与单词向量的长度成 \(O(|V|)\)关系，而 \(softmax\) 计算公式也很复杂

\[\sigma(\mathbf{z})_{j}=\frac{e^{z_{j}}}{\sum_{k=1}^{K} e^{z_{k}}} \quad \text { for } j=1, \ldots, K \]

所以计算太复杂了，为了简化计算，我们能否不遍历语料库呢？

什么是Negative Sampling(负采样)

对于一个样本，在之前的样本中，我们都是将与正确的结果作为训练结果拿去训练的。对于负采样，在语言模型中，假设中心词为 \(w\), 他周围的上下文共有 \(2m\) 个单词，记为 \(context(w)\) ,那个 \(w\) 与 \(context(w)\) 的对应就是一个正例，而负例（可以理解为错误的例子）就是我们取 \(n\) 个与 \(w\) 不同的单词 \(w_{i}, i=1,2, \ldots n\), 这些 \(w_{i}\) 与 \(context(w)\) 就构成了负样本，然后利用分类的思想，这就相当于一个二元分类问题，通过最优化这个分类问题求解模型的参数。

对于一个样本是正样本，我们用逻辑回归的模型计算是正样本的概率，这里我们用 \(v_{c}^{T} v_{w}\) 表示的是 单词向量 \(v_{c}\) 与 文本向量 \(v_{w}\) 的点积，点积越大，越相关，那么 \(P = 1\) 的概率就越大：

\[P(D=1 | w, c, \theta)=\sigma\left(v_{c}^{T} v_{w}\right)=\frac{1}{1+e^{\left(-v_{c}^{T} v_{w}\right)}} \]

Negative Sampling下的损失函数

假设我们的参数还用 \(\theta\) 来表示的话， 分别用 \(D\) 与 \(D'\) 表示正负样本集合

\[\theta=\underset{\theta}{\operatorname{argmax}} \prod_{(w, c) \in D} P(D=1 | w, c, \theta) \prod_{(w, c) \in D'} P(D=0 | w, c, \theta) \]

\[=\underset{\theta}{\operatorname{argmax}} \prod_{(w, c) \in D} P(D=1 | w, c, \theta) \prod_{(w, c) \in D'}(1-P(D=1 | w, c, \theta)) \]

\[\begin{array}{l}{=\underset{\theta}{\operatorname{argmax}} \sum_{(w, c) \in D} \log P(D=1 | w, c, \theta)+\sum_{(w, c) \in D'} \log (1-P(D=1 | w, c, \theta))} \\ {=\underset{\theta}{\operatorname{argmax}} \sum_{(w, c) \in D} \log \frac{1}{1+\exp \left(-u_{w}^{T} v_{c}\right)}+\sum_{(w, c) \in \tilde{D}} \log \left(1-\frac{1}{1+\exp \left(-u_{w}^{T} v_{c}\right)}\right)}\end{array} \\ =\underset{\theta}{\operatorname{argmax}} \sum_{(w, c) \in D} \log \frac{1}{1+\exp \left(-u_{w}^{T} v_{c}\right)}+\sum_{(w, c) \in D'} \log \left(\frac{1}{1+\exp \left(u_{w}^{T} v_{c}\right)}\right) \]

在上面的式子中，我们又将参数 \(\theta\) 替换成了 矩阵 \(\mathcal{V}\) 和 \(\mathcal{U}\) 列向量与行向量，分别表示输入与输出。

最大化似然函数，等价于最小化下面的目标函数：

\[J=-\sum_{(w, c) \in D} \log \frac{1}{1+\exp \left(-u_{w}^{T} v_{c}\right)}-\sum_{(w, c) \in D'} \log \left(\frac{1}{1+\exp \left(u_{w}^{T} v_{c}\right)}\right) \]

那么对于 skip-gram算法来说

对于每一个中心词 C 来说：(这里没有遍历每一个中心词)

\[J = -\log \sigma\left(u_{c-m+j}^{T} \cdot v_{c}\right)-\sum_{k=1}^{K} \log \sigma\left(-\tilde{u}_{k}^{T} \cdot v_{c}\right) \]

对于CBOW算法，\(\hat{v}=\frac{v_{c-m}+v_{c-m+1}+\ldots+v_{c+m}}{2 m}\) 还是用这个公式，所以损失函数就可以写成：

\[J = -\log \sigma\left(u_{c}^{T} \cdot \hat{v}\right)-\sum_{k=1}^{K} \log \sigma\left(-\tilde{u}_{k}^{T} \cdot \hat{v}\right) \]

Hierarchical Softmax​

分层 \(Softmax\) 在用于非连续的单词向量的时候，表现比较好。而负采样用于连续的单词向量的时候表现比较好。分层 \(Softmax\) 使用的是哈夫曼树。

我们使用叶子结点代表每一个单词，单词的概率定位为从根节点随机走到该节点的概率。由于是二叉树，我们结算复杂度为 \(O(\log (|V|))\)。这样就降低了模型的复杂度，而我们要学习的参数，就是除了叶节点之外的权重。我们用 \(L(w)\) 表示从根结点到叶结点的长度，比如图中的 \(L(w2)\) = 3. 而我们用 \(n(w, i)\) 表示路径上的第 \(i\) 个结点，对应于向量中的参数就是 \(v_{n(w, i)}\)。对于结点 \(n\) 我们用 \(\operatorname{ch}(n)\) 表示 \(n\) 的孩子结点，那么叶结点是 \(w\)的概率就是：

\[P\left(w | w_{i}\right)=\prod_{j=1}^{L(w)-1} \sigma\left([n(w, j+1)=\operatorname{ch}(n(w, j))] \cdot v_{n(w, j)}^{T} v_{w_{i}}\right) \]

其中

\[[x]=\left\{\begin{array}{l}{1 \text { if } x \text { is true }} \\ {-1 \text { otherwise }}\end{array}\right. \]

上面的式子，对于某个结点 \(i\) ,如果 \(n(w, i+1)\) 就是 \(n(w, i)\) 的孩子的节点的的话，那么 \([x] = 1\)，否则 \([x] = -1\) ,这里的 +1 或者 -1 仅仅是用来表示叶结点的方向。对于上图中的例子来说就是：

\[\begin{aligned} P\left(w_{2} | w_{i}\right) &=p\left(n\left(w_{2}, 1\right), \text { left }\right) \cdot p\left(n\left(w_{2}, 2\right), \text { left }\right) \cdot p\left(n\left(w_{2}, 3\right), \text { right) }\right.\\ &=\sigma\left(v_{n\left(w_{2}, 1\right)}^{T} v_{w_{i}}\right) \cdot \sigma\left(v_{n\left(w_{2}, 2\right)}^{T} v_{w_{i}}\right) \cdot \sigma\left(-v_{n\left(w_{2}, 3\right)}^{T} v_{w_{i}}\right) \end{aligned} \]

而且我们可以保证：

\[\sum_{w=1}^{|V|} P\left(w | w_{i}\right)=1 \]

可以看出，对于每一次更新语料库，不需要重新计算全部，而是计算，新的 word 对应的 Path 中的参数就可以了。