HDU1402（FFT入门）
题目链接：http://acm.hdu.edu.cn/status.php?user=Reykjavik11207&pid=1402&status=5
本题数据范围为5e4，常规方法O(n2)肯定是不行的。
FFT是离散傅里叶变换DFT的快速形式
对多项式f(x) = a0 + a1x + a2x2 + ··· +an-1xn-1，有两种表示法：
系数表达式 ： (a0 , a1 , ··· , an-1)
由于n-1次多项式需要n个点来确定
所以可以用点值表达式 ： ( (x0,f(x0)) , (x1,f(x1)) , ··· , (xn-1,f(xn-1)) ) 来表示
要获得点值表达式，首先选取n个x值获得对应f(x)的值
将f(x)分为奇偶两个部分f(x) = a0 + a2x2 + ··· + an-2xn-2 + a1x + a3x3 + ··· + an-1xn-1，
令f1(x) = a0 + a2x + ··· + an-2 x(n-2)/2，
f2(x) = a1 + a3x + ··· + an-1 x(n-1)/2，
则有f(x) = f1(x2) + xf2(x2)
f1(x)与f2(x)再分别分解，直至到常数ai为止
到了这里，复杂度并没有降低，反而由于x的整次幂未知还升高了，可以发现x = 1可以使式子更简单，因为1的多少次幂都是1，然后就是-1，但只有2个数远远不够，所以引入了复数。
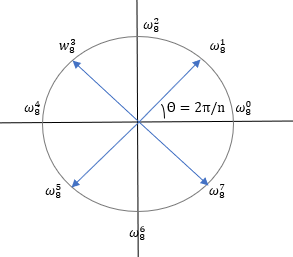
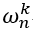是复平面单位圆上逆时针按k从小到大均匀分布的复根，间隔角度为2π/n，所以有：
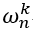= cos(2kπ/n) + i * sin(2kπ/n) ，计算复根的k次幂显然较实数更为方便，（但STL中三角函数也不是O(1)，是多少我也不太懂，总之我把wnk函数放三重循环里就超时了）。
容易看出它的周期为n，即满足
同时还有以下性质：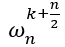
= cos(2kπ/n + π) + i * sin(2kπ/n + π) =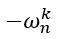 
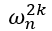= cos(2*2k*π/n) + i * sin(2*2k*π/n) = cos(2kπ/(n/2)) + i * sin(2kπ/(n/2)) =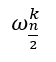 
故f(wnk+n/2) = f1(wn/2k) - wnk f2(wn/2k)
以n = 4为例：
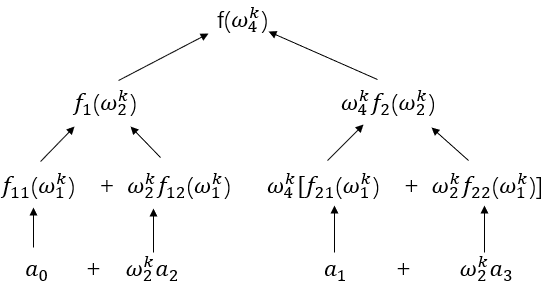
显然n必须为2的整数次幂
原来第i个元素的位置经过变换后的位置为i的二进制按长度翻转，
如上图中(0)10 = (00)2 翻转 -> (00)2 = (0)10，
(1)10 = (01)2 翻转 -> (10)2 = (2)10 ，
(2)10 = (10)2 翻转-> (01)2 = (1)10 ，
(3)10 = (11)2 翻转-> (11)2 = (3)10 ，
然后自底向上代入函数中，得到n个f(x)值
另一个数同理得到n个g(x)值
令F(x) = f(x)*g(x)，则F(xi) = f(xi)*g(xi)
接下来就要用傅里叶逆变换IDFT求出F(x)的系数表达式
变换矩阵
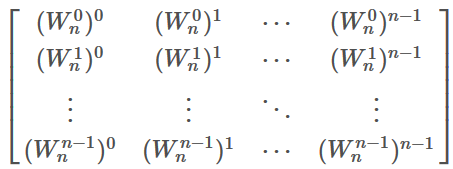
的逆矩阵为
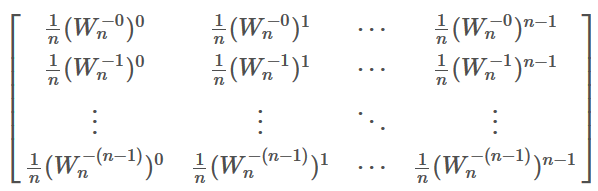
进而得到F(x)的系数表达式，即为结果
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1 << 17;
const double pi = acos(-1.0);
const double eps = 1e-4;//这个...精度问题，本来用的1e-8就WA了
int n,len;
int rev(int x)//二进制翻转
{
int res = 0;
for(int i = 0; i < len; i++)
res += ((x >> i) & 1) << (len - 1 - i);
return res;
}
struct Complex
{
double real,image;
Complex(double r = 0,double i = 0)
{
real = r;
image = i;
}
Complex operator + (const Complex &t)
{
return Complex(real + t.real, image + t.image);
}
Complex operator - (const Complex &t)
{
return Complex(real - t.real, image - t.image);
}
Complex operator * (const Complex &t)
{
return Complex(real * t.real - image * t.image, real * t.image + t.real * image);
}
};
Complex wnk(double n,double k)
{
return Complex(cos(2*pi*k/n), sin(2*pi*k/n));
}
void fft(Complex y[], int dft)
{
Complex t1,t2;
for(int i = 1; i < n; i <<= 1)
{
Complex W(1,0), w = wnk(2*i,dft);
for(int k = 0; k < i; k++)
{
for(int j = k; j < n; j += i<<1)
{
t1 = y[j] + W * y[j+i];
t2 = y[j] - W * y[j+i];
y[j] = t1;
y[j+i] = t2;
}
W = W * w;
}
}
if(dft == -1)
{
for(int i = 0; i < n; i++)
y[i].real /= n;
}
}
Complex a1[N],a2[N],a[N];
int ans[N];
char stra[N>>1],strb[N>>1];
int main()
{
while(~scanf("%s %s",stra,strb))
{
int lena = strlen(stra);
int lenb = strlen(strb);
len = log10(lena+lenb)/log10(2) + 1 + eps;
n = 1 << len;
for(int i = 0; i < lena; i++)
a1[rev(i)] = Complex((double)(stra[lena-i-1] - '0'), 0);
for(int i = lena; i < n; i++)
a1[rev(i)] = Complex(0,0);
for(int i = 0; i < lenb; i++)
a2[rev(i)] = Complex((double)(strb[lenb-i-1] - '0'), 0);
for(int i = lenb; i < n; i++)
a2[rev(i)] = Complex(0,0);
fft(a1,1);
fft(a2,1);
for(int i = 0; i < n; i++)
a[rev(i)] = a1[i] * a2[i];
fft(a,-1);
int t = 0;
for(int i = 0; i < n; i++)
{
ans[n - 1 - i] = ((int)(a[i].real + eps) + t) % 10;
t = ((int)(a[i].real + eps) + t) / 10;
}
bool flag = 0;
for(int i = 0; i < n - 1; i++)
{
if(ans[i])
flag = 1;
if(!flag)
continue;
printf("%d",ans[i]);
}
printf("%d\n",ans[n-1]);
}
return 0;
}
⎢⎢⎢(W
