2D、3D 线性坐标系变换

坐标系

2D坐标系

左上坐标系

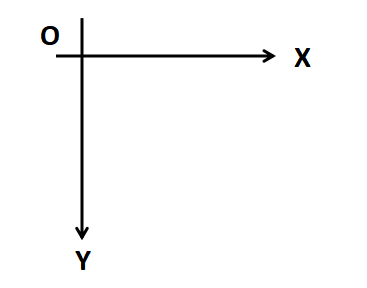
常用于图像处理。图像在显示器上显示，可以把图像看作矩阵，矩阵的每一个元素值对应图像同位置的像素值。
图像处理，比如旋转、缩放、平移等，都可以通过矩阵变换来实现。

正交直角坐标系

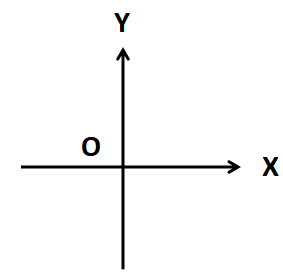
一般人眼习惯的坐标系。

3D坐标系

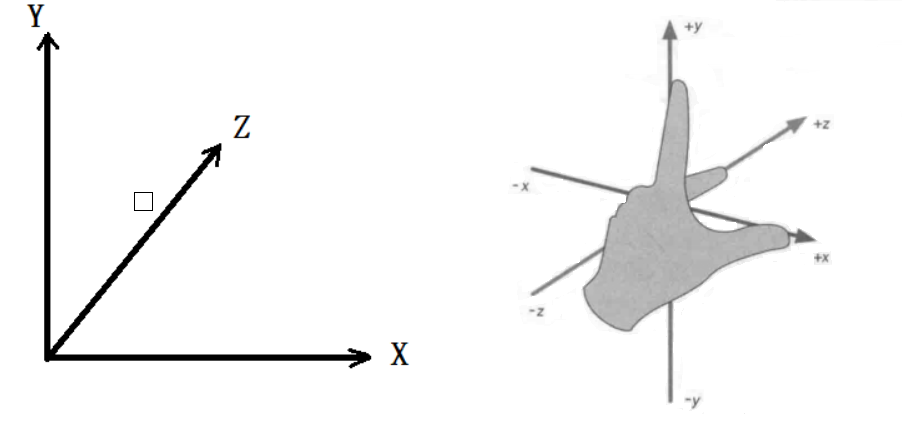
空间直角坐标系

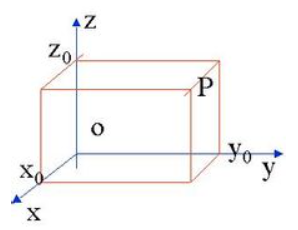
位于X，Y，Z轴的正半轴的卦限称为第一卦限。

右手坐标系

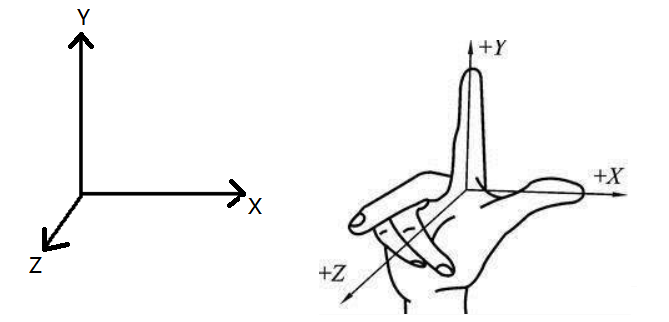
左手坐标系

线性转换

2D转换

任意坐标系的坐标转换，都可通过旋转Rotation、缩放Scaling、平移Translation等转换为线性变换。

旋转+缩放+平移

$$\begin{aligned} \begin{pmatrix} X'\\ Y' \end{pmatrix} &= \begin{bmatrix} \cos\theta_{x} & -\sin\theta_{y} \\ \sin\theta_{x} & \cos\theta_{y} \end{bmatrix} \begin{bmatrix} S_{x} & 0 \\ 0 & S_{y} \end{bmatrix} \begin{pmatrix} X\\ Y \end{pmatrix} + \begin{pmatrix} T_{x} \\ T_{y} \end{pmatrix} \\ &= \begin{bmatrix} S_{x}\cos\theta_{x} & -S_{y}\sin\theta_{y} \\ S_{x}\sin\theta_{x} & S_{y}\cos\theta_{y} \end{bmatrix} \begin{pmatrix} X\\ Y \end{pmatrix} + \begin{pmatrix} T_{x} \\ T_{y} \end{pmatrix} \end{aligned}$$

其中
Sx/Sy, x/y轴缩放比例；
$\theta_{x}/\theta_{y}$，x/y轴旋转度数（顺时针）；
Tx/Ty，x/y轴平移量（参考原点在新坐标系中的值）；

比如，图像坐标系 转为 居中的直角坐标系表示。

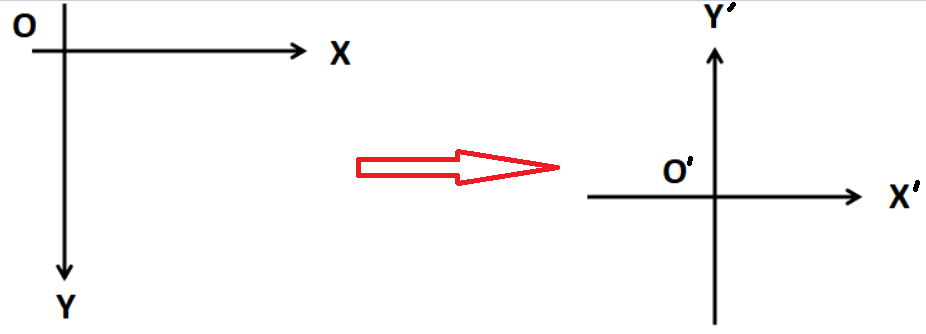
根据上述公式，确定相关参数，带入公式计算即可。

源坐标系	目标坐标系	备注
$\theta_{x}$	0	X轴方向不变，即为X'轴
$\theta_{y}$	180°	Y轴顺时针旋转180°变成Y'
Sx	1	X轴没有缩放
Sy	1	Y轴没有缩放
Tx	$-\frac{width}{2}$	参考原点O在目标坐标系的X'轴上的值，其中width为图像的像素宽
Ty	$\frac{height}{2}$	参考原点O在目标坐标系的Y'轴上的值，其中height为图像的像素高

源坐标系某一像素位置(x,y),转换后在目标坐标系中的位置x',y'的值分别为：
$x'=x-\frac{width}{2} ,\ y'=-y+\frac{height}{2}$

倾斜 Shearing

转换逻辑：旋转 -> 倾斜 -> 均匀缩放 -> 长宽比

$$\begin{aligned} \begin{pmatrix} X'\\ Y' \end{pmatrix} &= \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} \begin{bmatrix} 1 & -\sin Q \\ 0 & \cos Q \end{bmatrix} \begin{bmatrix} S & 0 \\ 0 & S \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 0 & A \end{bmatrix} \begin{pmatrix} X\\ Y \end{pmatrix} + \begin{pmatrix} T_{x} \\ T_{y} \end{pmatrix} \\ &= \begin{bmatrix} S\cos\theta & -S\sin(Q+\theta) \\ S\sin\theta & SA\cos(Q+\theta) \end{bmatrix} \begin{pmatrix} X\\ Y \end{pmatrix} + \begin{pmatrix} T_{x} \\ T_{y} \end{pmatrix} \end{aligned}$$

其中
S, x/y轴统一缩放比例；
$\theta$，x/y轴均匀旋转度数（顺时针）；
A，纵横比（以x轴为单位，比如宽为1，y轴的相对值）；
Q，倾斜角度数；
Tx/Ty，x/y轴平移量（参考原点在新坐标系中的值）；

Matrix

System.Drawing.Drawing2D.Matrix，代表一个GDI矩阵，一般用在Windows窗体（Winform）中，展示几何变换。
System.Windows.Media也定义有Matrix，不过System.Windows命名空间中类一般用于WPF
在GDI+中，可以将仿射变换（旋转、放缩、平移）存储在Matrix中（3X3），如图所示复合变换的矩阵：

Matrix matrix = new Matrix(0, 1, -1, 0, 3, 4);

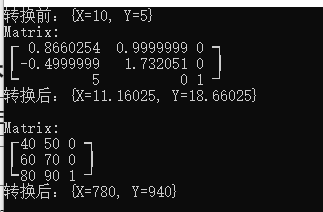
using System;
using System.Drawing;
using System.Drawing.Drawing2D;
using System.Linq;

var pt = new PointF(10, 5);
Console.WriteLine("转换前：" + pt);
var matrix = new Matrix();
matrix.Rotate(30);
matrix.Scale(1, 2, MatrixOrder.Append);
matrix.Translate(5, 0, MatrixOrder.Append);
Console.WriteLine("Matrix: ");
PrintMatrix(matrix);
var arr = new PointF[] { pt };
matrix.TransformPoints(arr);
Console.WriteLine("转换后：" + arr[0]);

Console.WriteLine(Environment.NewLine + "Matrix: ");
matrix = new Matrix(40, 50, 60, 70, 80, 90);
PrintMatrix(matrix);
pt = new PointF(10, 5);
PointF[] arr2 = { pt };
matrix.TransformPoints(arr2);
Console.WriteLine("转换后：" + arr2[0]);

static void PrintMatrix(Matrix matrix)
{
	var arr = matrix.Elements;
	var pad = arr.Max(s => s.ToString().Length);
	StringBuilder sb = new StringBuilder();
	// 占位符
	var pattern = $"{{0,{pad}}}";
	sb.AppendLine($"┎ {string.Format(pattern, arr[0])} {string.Format(pattern, arr[1])} 0 ┑");
	sb.AppendLine($"┃ {string.Format(pattern, arr[2])} {string.Format(pattern, arr[3])} 0 ┃");
	sb.AppendLine($"┕ {string.Format(pattern, arr[4])} {string.Format(pattern, arr[5])} 1 ┘");
	Console.Write(sb.ToString());
}

3D转换

3D线性转换相对复杂。
依据右手螺旋定则 x -> y -> z -> x......

单轴旋转

旋转Z轴
Z轴旋转$\theta$，即Z轴不变，X轴向Y轴旋转$\theta$。

$$\begin{aligned} \begin{pmatrix} X'\\ Y'\\ Z' \end{pmatrix} &= \begin{bmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{pmatrix} X\\ Y\\ Z \end{pmatrix} \end{aligned}$$

旋转X轴
X轴旋转$\theta$，即X轴不变，Y轴向Z轴旋转$\theta$。

$$\begin{aligned} \begin{pmatrix} X'\\ Y'\\ Z' \end{pmatrix} &= \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta \\ 0 & \sin\theta & \cos\theta \end{bmatrix} \begin{pmatrix} X\\ Y\\ Z \end{pmatrix} \end{aligned}$$

旋转Y轴
Y轴旋转$\theta$，即Y轴不变，Z轴向X轴旋转$\theta$。

$$\begin{aligned} \begin{pmatrix} X'\\ Y'\\ Z' \end{pmatrix} &= \begin{bmatrix} \cos\theta & 0 & \sin\theta \\ 0 & 1 & 0 \\ -\sin\theta & 0 & \cos\theta \end{bmatrix} \begin{pmatrix} X\\ Y\\ Z \end{pmatrix} \end{aligned}$$

缩放

$$\begin{aligned} \begin{pmatrix} X'\\ Y'\\ Z' \end{pmatrix} &= \begin{bmatrix} S_{x} & 0 & 0 \\ 0 & S_{y} & 0 \\ 0 & 0 & S_{z} \end{bmatrix} \begin{pmatrix} X\\ Y\\ Z \end{pmatrix} \end{aligned}$$

倾斜
以X轴为基准，在Y轴、Z轴上拉伸。

$$\begin{aligned} \begin{pmatrix} X'\\ Y'\\ Z' \end{pmatrix} &= \begin{bmatrix} 1 & d_{y} & d_{z} \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{pmatrix} X\\ Y\\ Z \end{pmatrix} \end{aligned}$$

其中，dy是Y轴上的拉伸比，dz是Z轴上的拉伸比。

任意轴旋转

绕任意经过原点的轴进行旋转

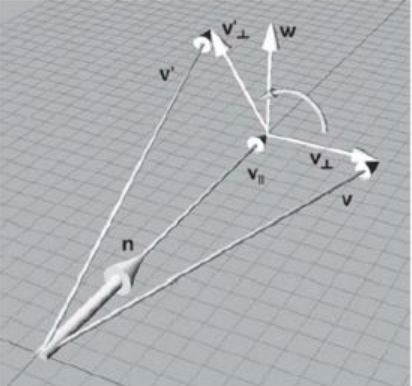
如图所示，绕N轴旋转$\theta$，向量n的旋转结果为：

$$\begin{aligned} R(n,\theta ) &= \begin{pmatrix} X' \\ Y' \\ Z' \end{pmatrix} \\ &= \begin{bmatrix} n_{x}^{2}(1-\cos\theta)+\cos\theta & n_{x}n_{y}(1-\cos\theta)-n_{z}\sin\theta & n_{x}n_{z}(1-\cos\theta)+n_{y}\sin\theta \\ n_{x}n_{y}(1-\cos\theta)+n_{z}\sin\theta & n_{y}^2(1-\cos\theta)+\cos\theta & n_{y}n_{z}(1-\cos\theta)-n_{z}\sin\theta \\ n_{x}n_{z}(1-\cos\theta)-n_{y}\sin\theta & n_{y}n_{z}(1-\cos\theta)+n_{x}\sin\theta & n_{z}^2 (1-\cos\theta)+\cos\theta \end{bmatrix} \begin{pmatrix} X \\ Y \\ Z \end{pmatrix} \end{aligned}$$