软件设计师：数据结构
复杂度
大O表示法
时间复杂度
空间复杂度
定义的数据占用多少空间就是空间复杂度
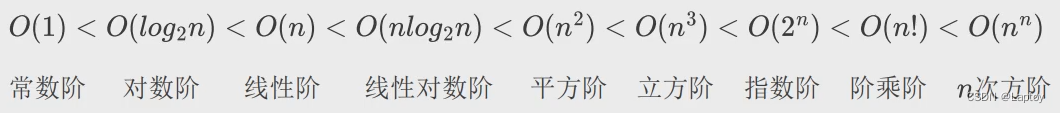
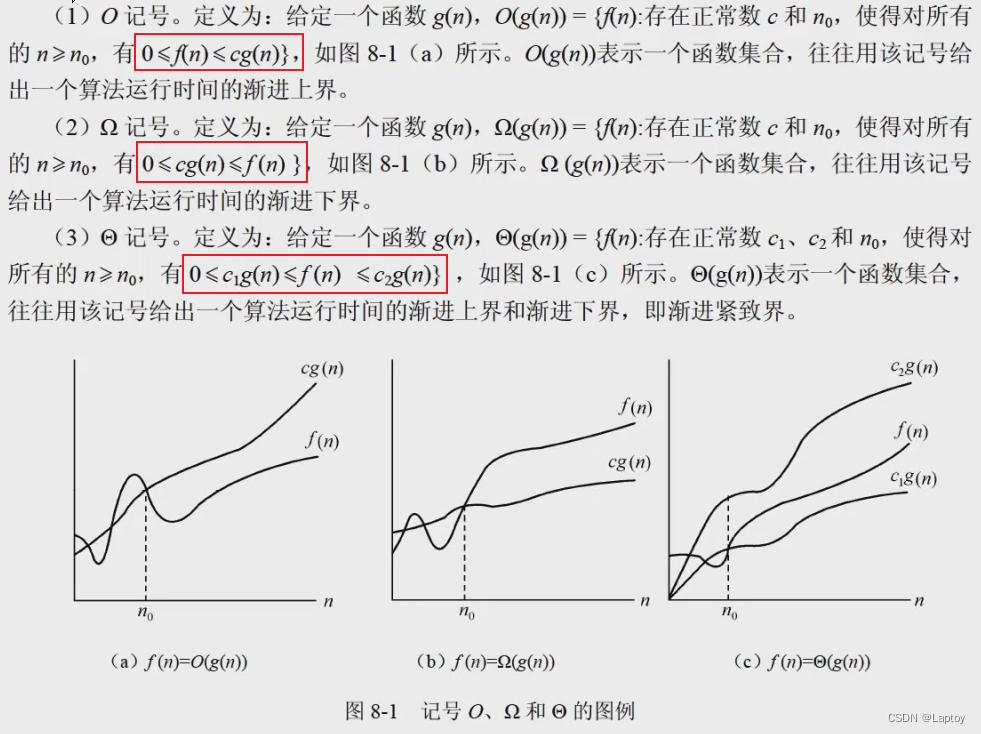
渐进符号 了解 直接蒙吧
递归
复杂度
递归式 看不懂
线性结构
定义
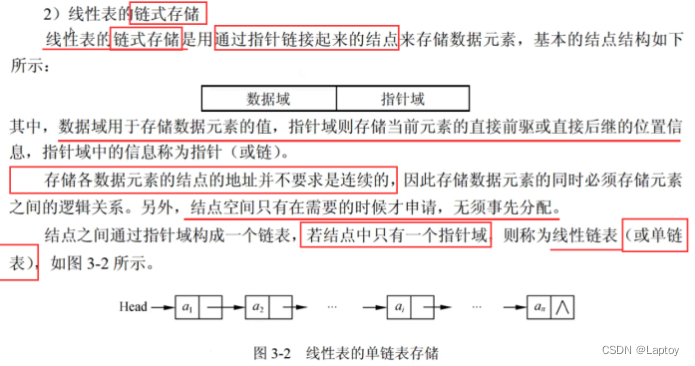
线性表的存储结构
通过索引快速查询到线性表中的元素，效率高，但是插入和删除会批量移动，效率低；查询快，增删慢
- 顺序存储插入元素需要移动的元素个数：n/2
- 顺序存储删除元素需要移动的元素个数：(n-1)/2
顺序存储
插入元素
- 最好的情况就是直接在顺序表后面插入一个元素，时间复杂度为O(1)
- 最坏的情况是在插入一个元素到原来第一个元素的位置，时间复杂度为O(n)
- 平均复杂度为O(n)
删除元素
- 最好的情况就是直接在删除最后一个元素，时间复杂度为O(1)
- 最坏的情况是删除第一个元素，时间复杂度为O(n)
- 平均复杂度为O(n)
查找元素
时间复杂度为O(1)
链式存储
插入元素
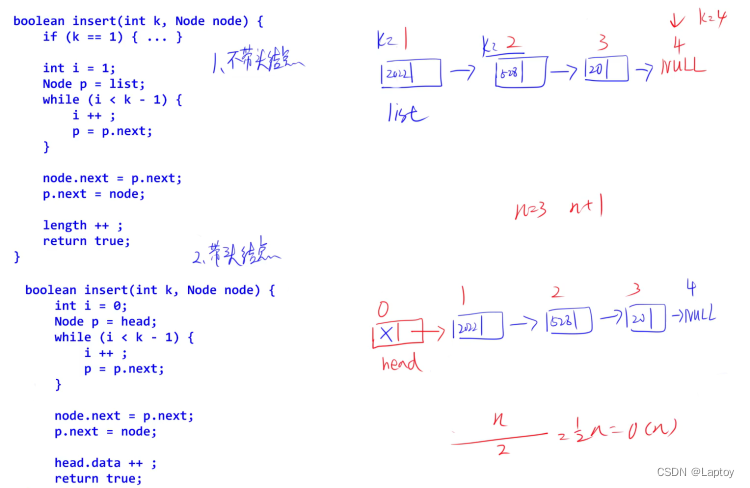
删除元素
查找元素
栈
先进后出
用栈实现递归调用
不需要遍历链表就能入栈/出栈操作
队列
先进先出
不需要遍历链表就能入队/出队操作
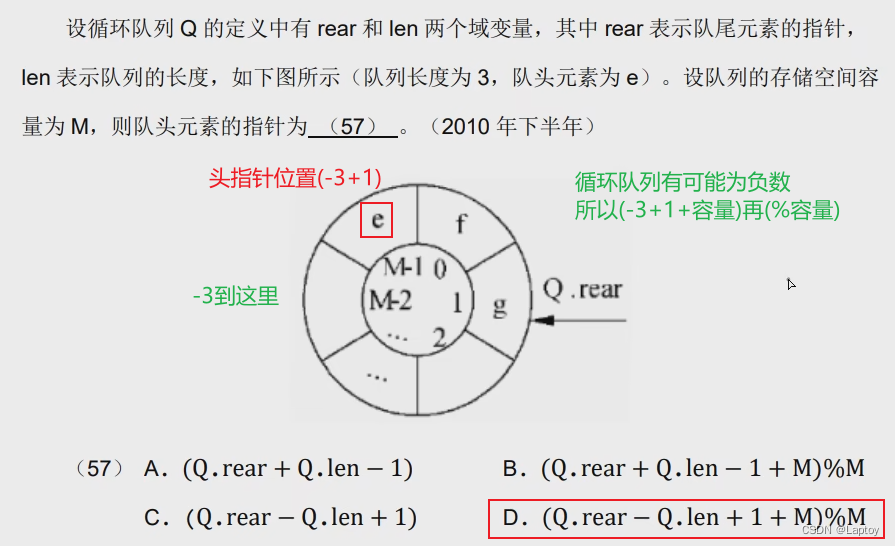
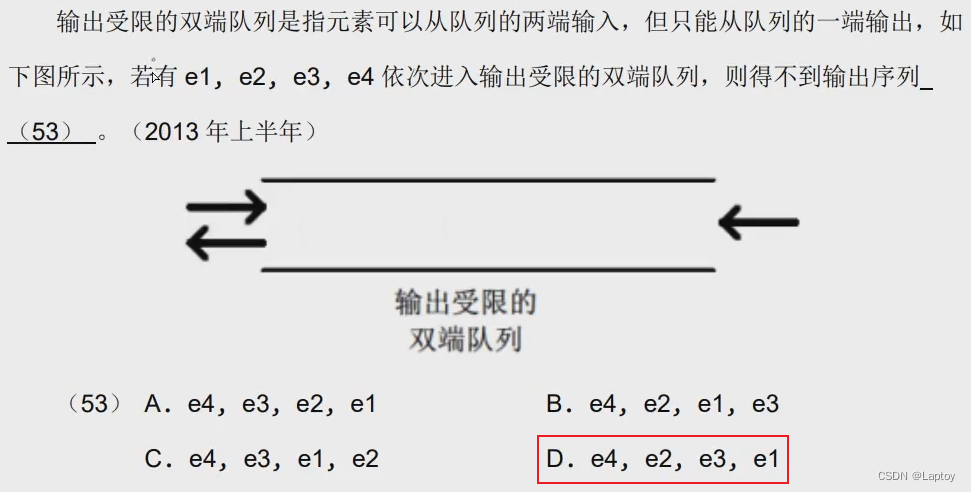
栈+队列的题
入队和出队序列一定相同，入栈和出栈序列不一定相同
串 了解 出了就不要了
字符构成的序列
- 空串：长度为0的串
- 空格串：由空格组成的串
举个例子试
串的模式匹配和朴素匹配 了解 出了就不要了
数组
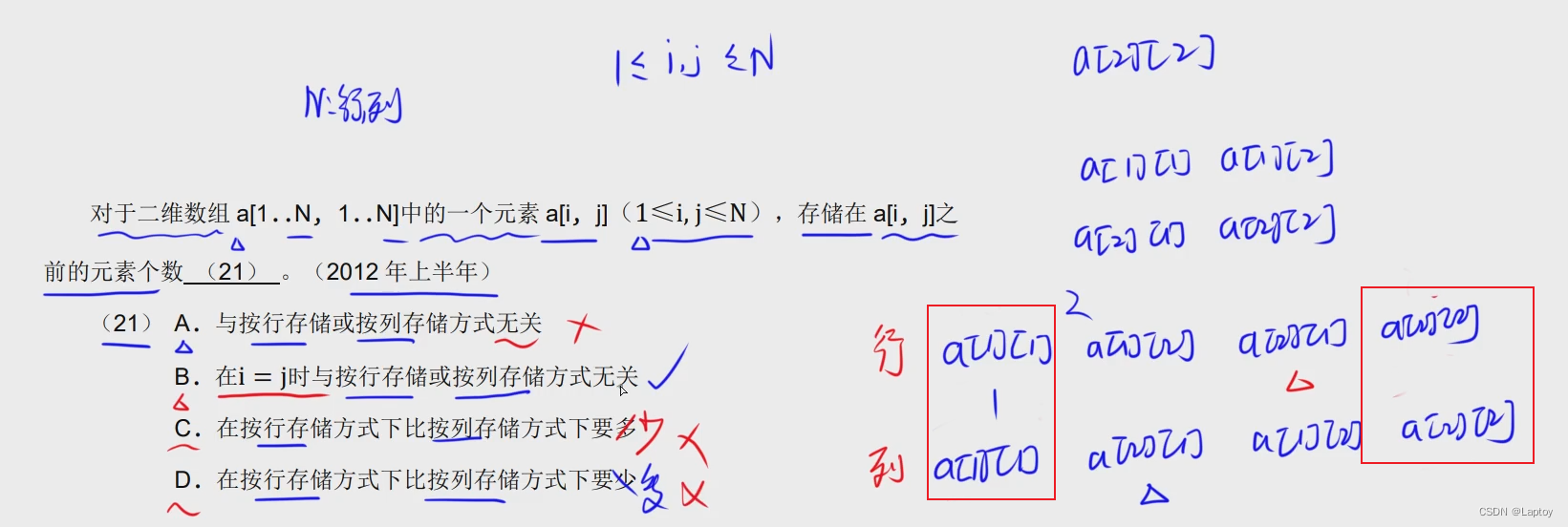
矩阵 代入法
对称矩阵
只存储下三角区
A[i,j]=A[j,i]
三对角矩阵
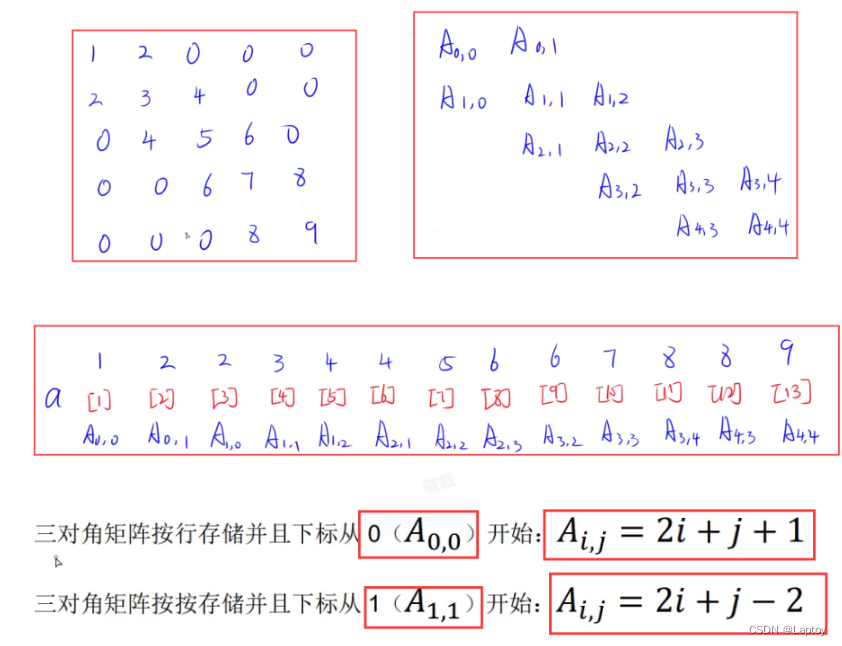
左下、右上为0 可不存储
稀疏矩阵
做题技巧：按行存储 每行开始 1 2 3 ... n
A[1,1]=3 代入验算
A[1,2]=2 代入验算
纯背
树
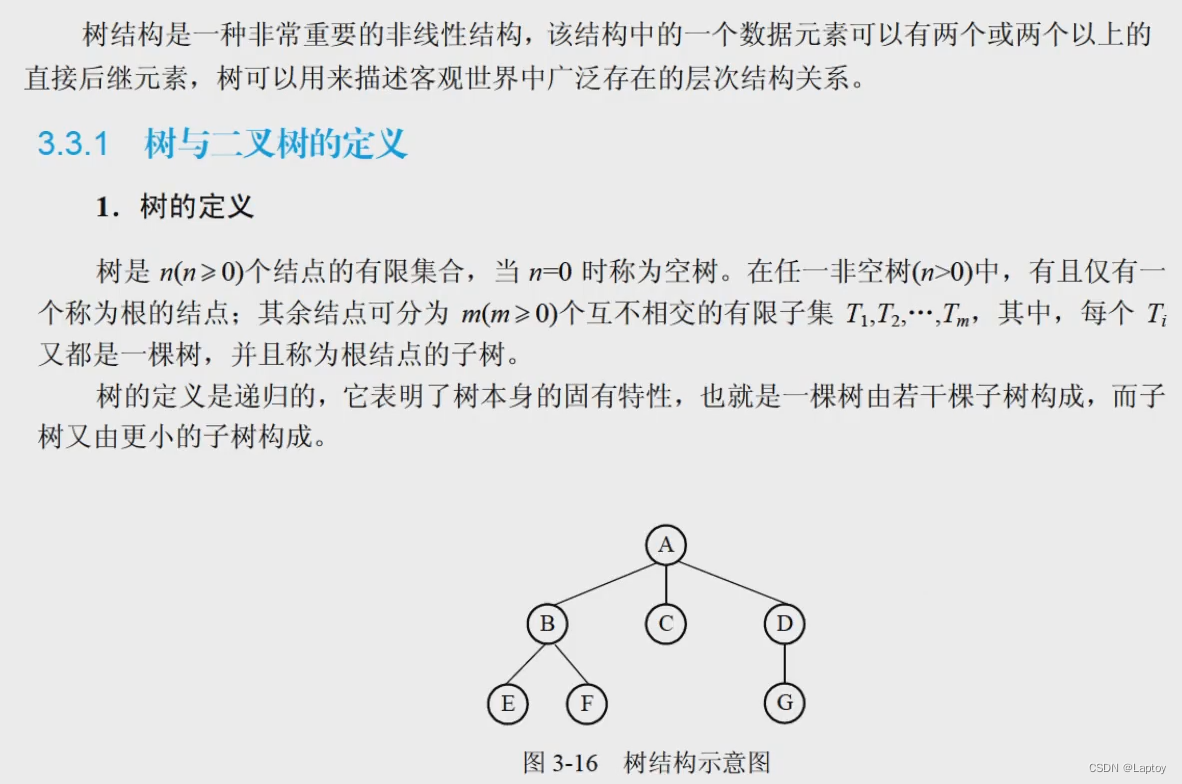
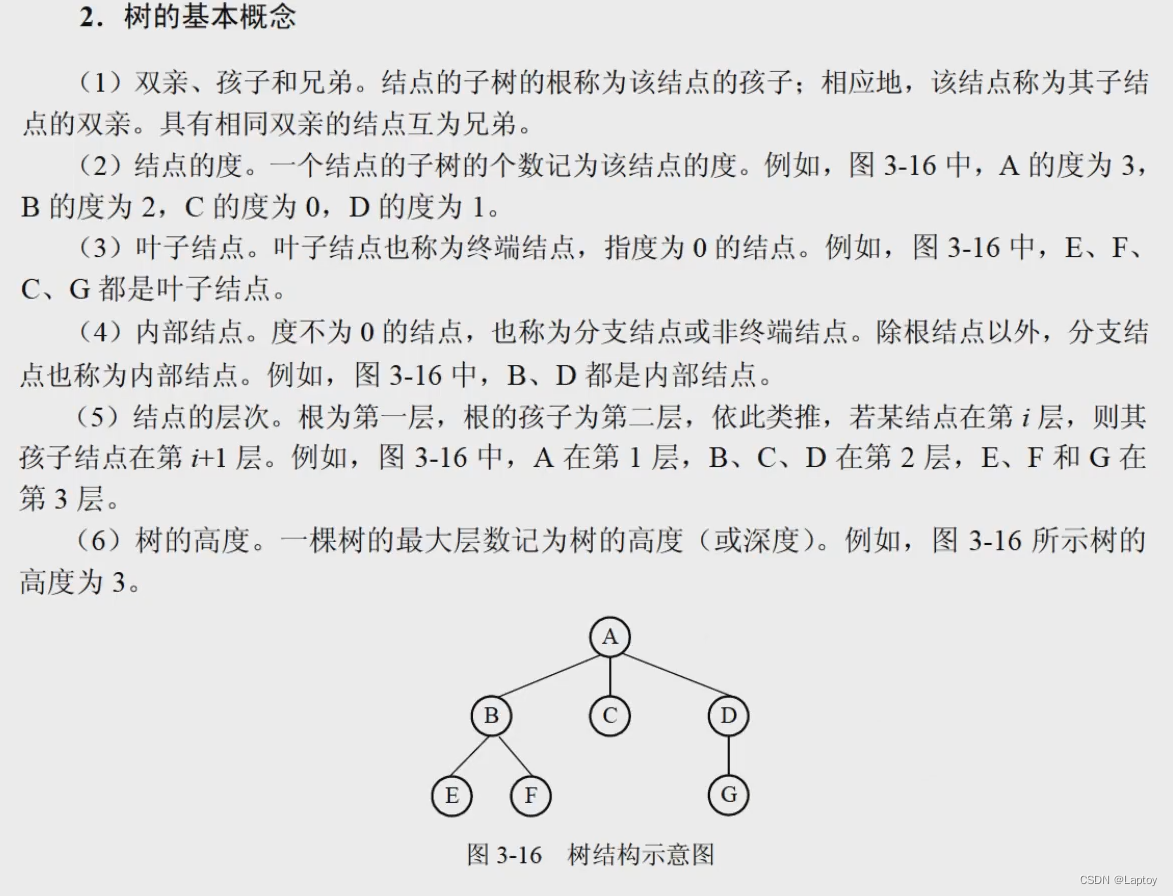
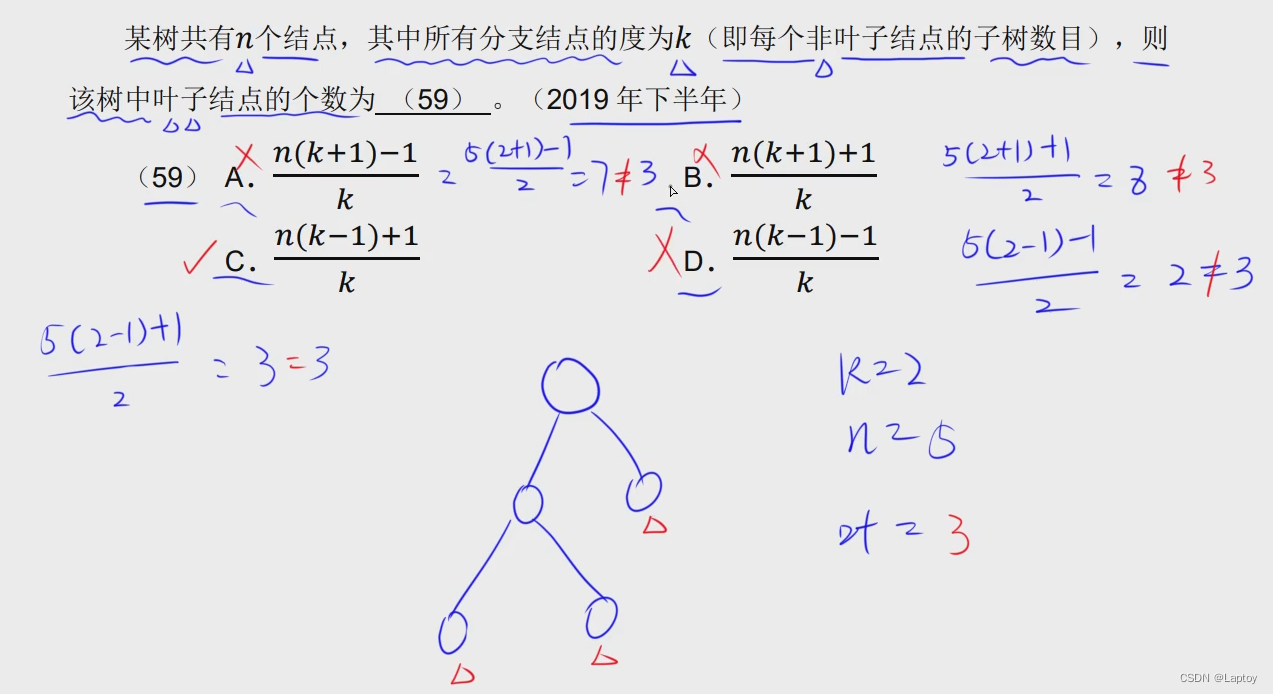
- 度：结点的子结点个数
- 树的度：所有结点的度的最大值
- 高度(深度)：树的高度
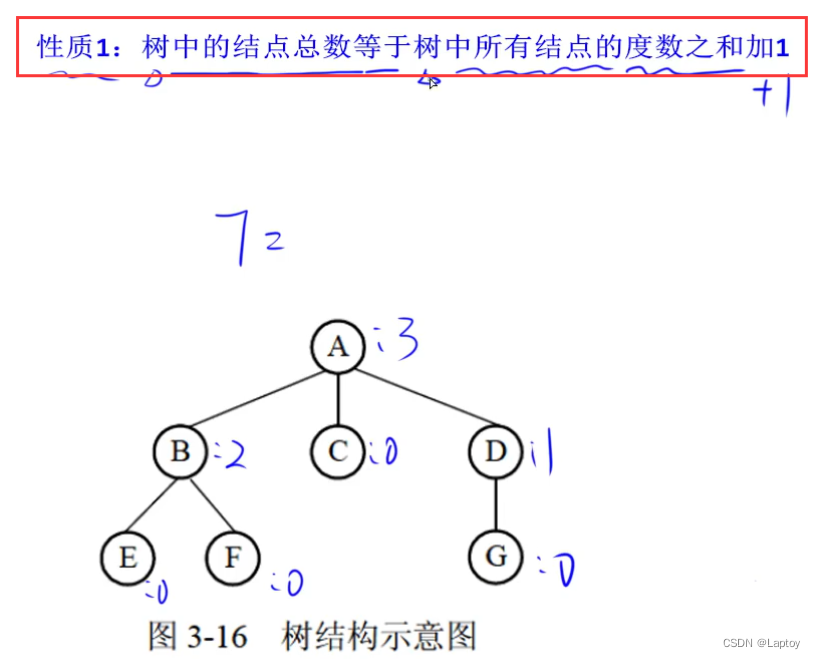
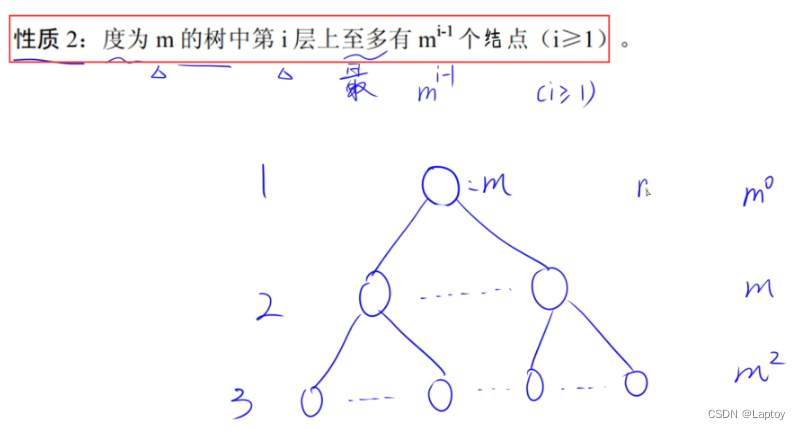
保证每个结点都有m个子结点
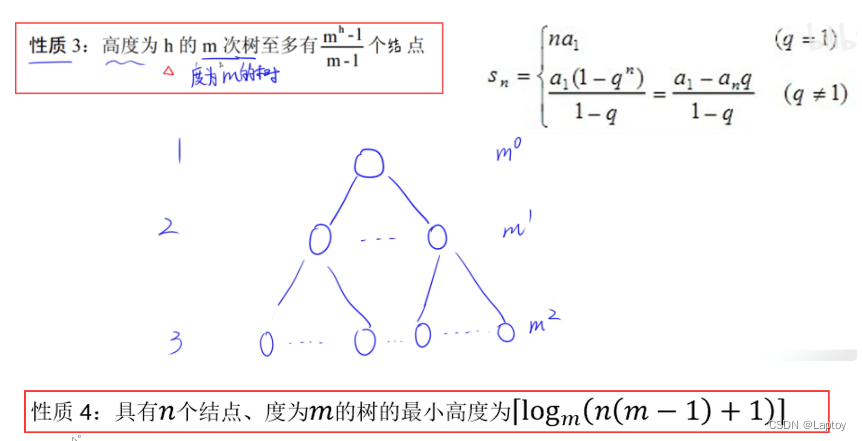
记不住公式就代入法
二叉树
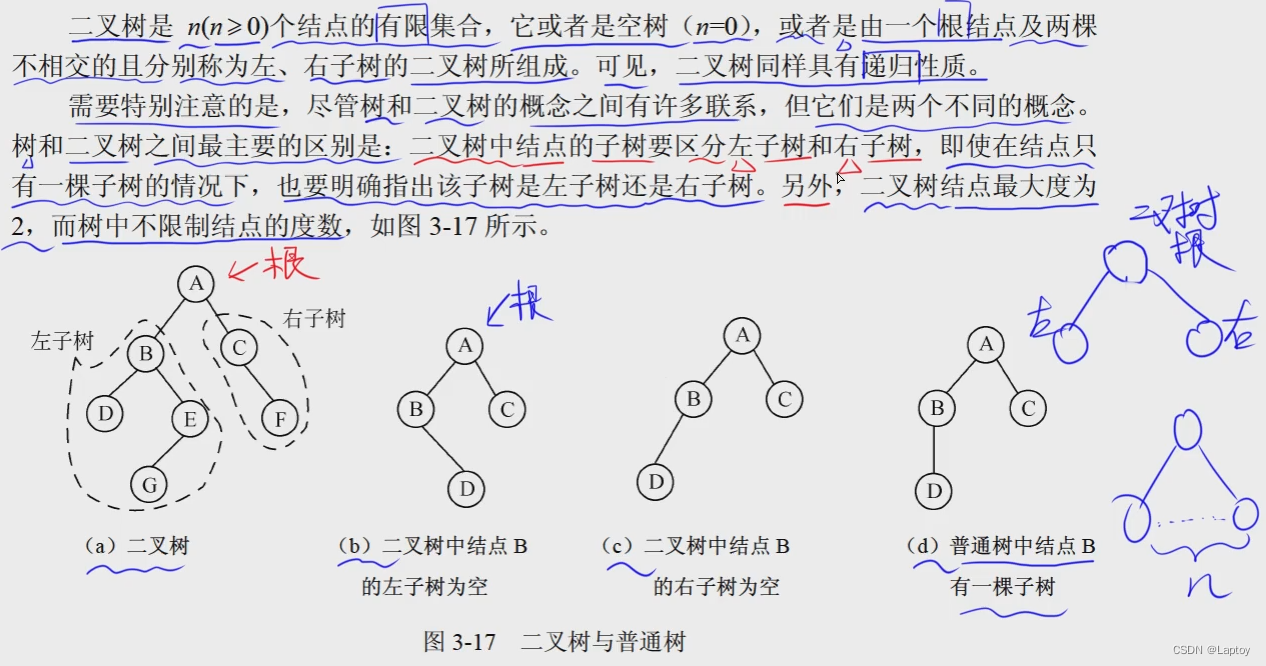
度最大为2
-
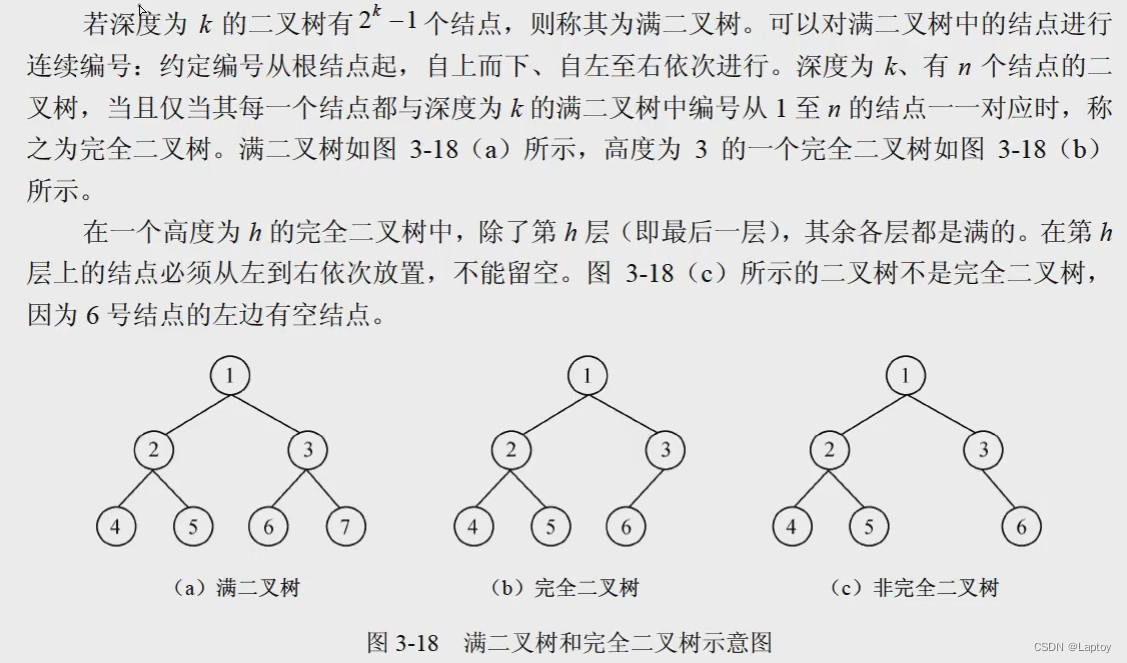
满二叉树：叶子结点外的结点的度均为2
-
完全二叉树：从根结点起，从上到下、从左到右依次填满结点的二叉树
记不住公式就代入法
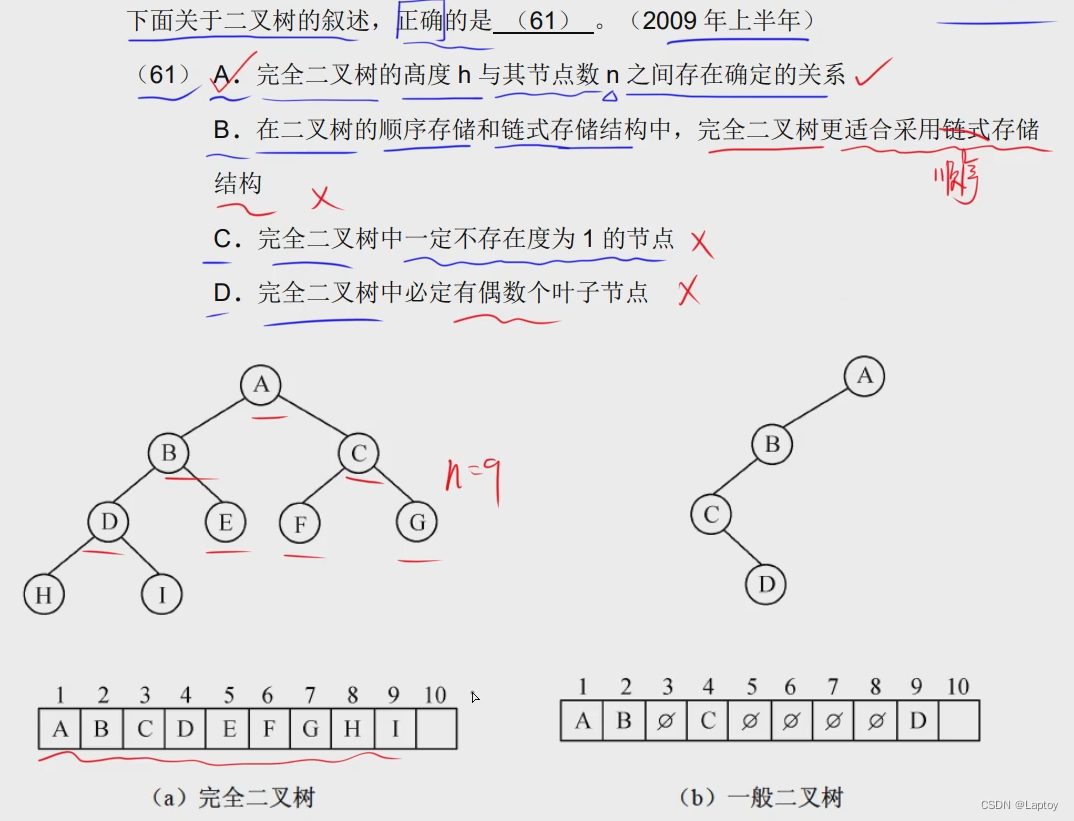
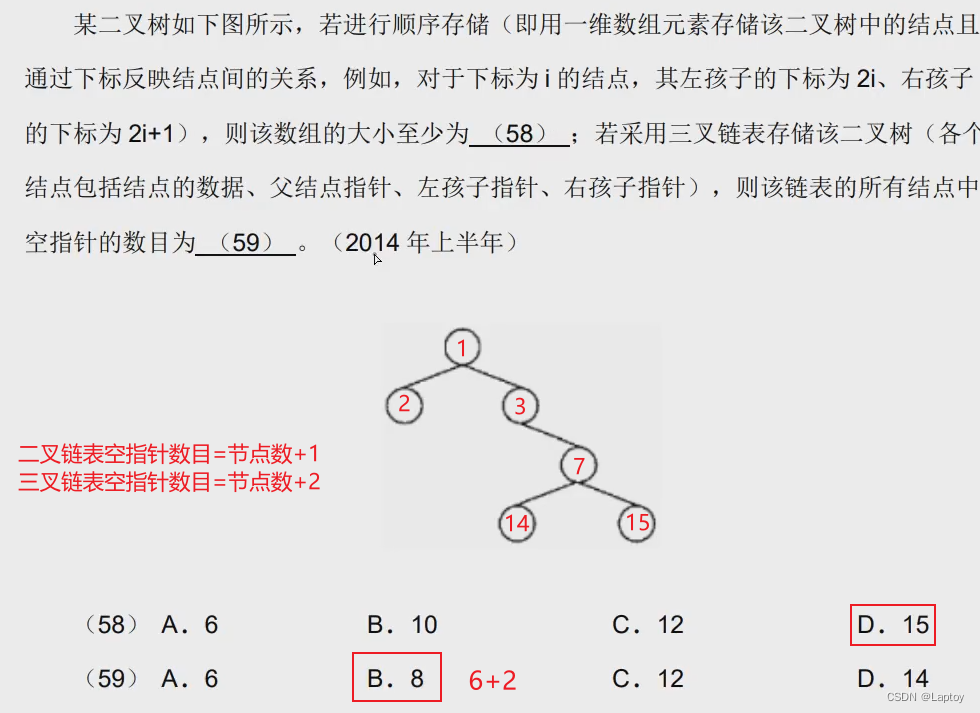
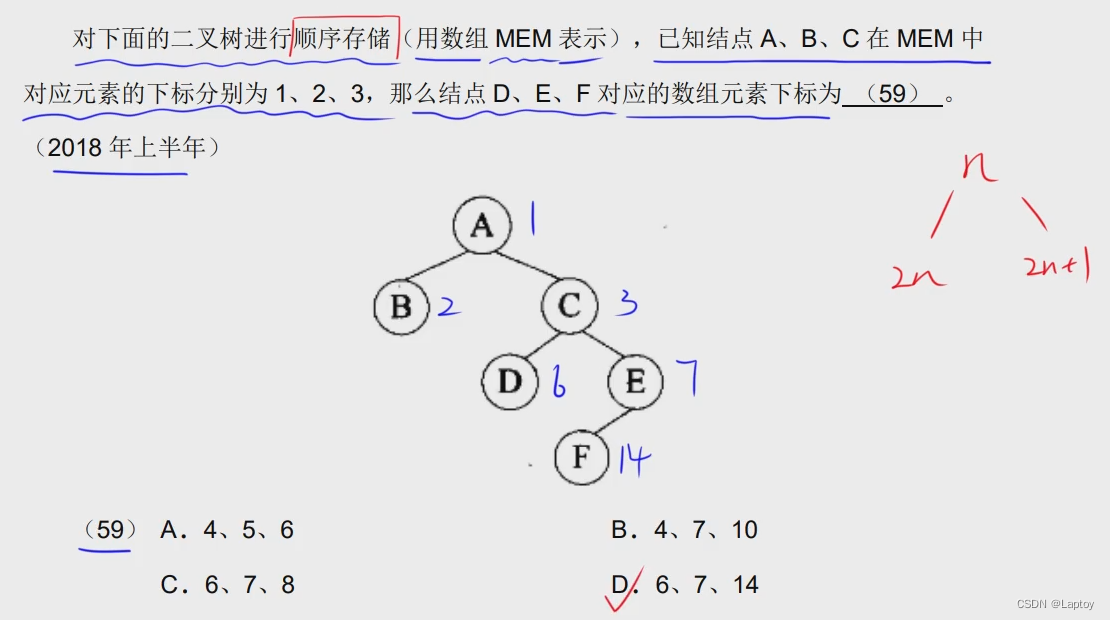
二叉树顺序存储结构
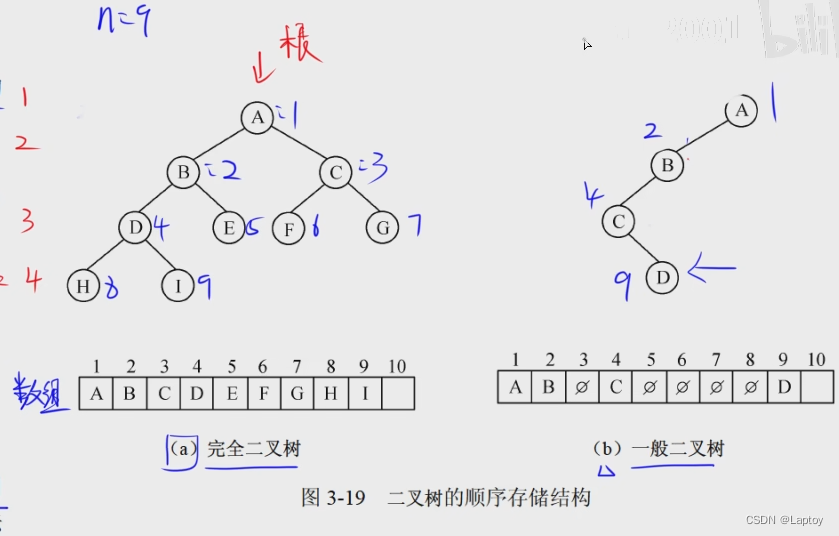
非完全二叉树没结点的地方也占用空间，造成空间浪费
二叉树链式存储结构
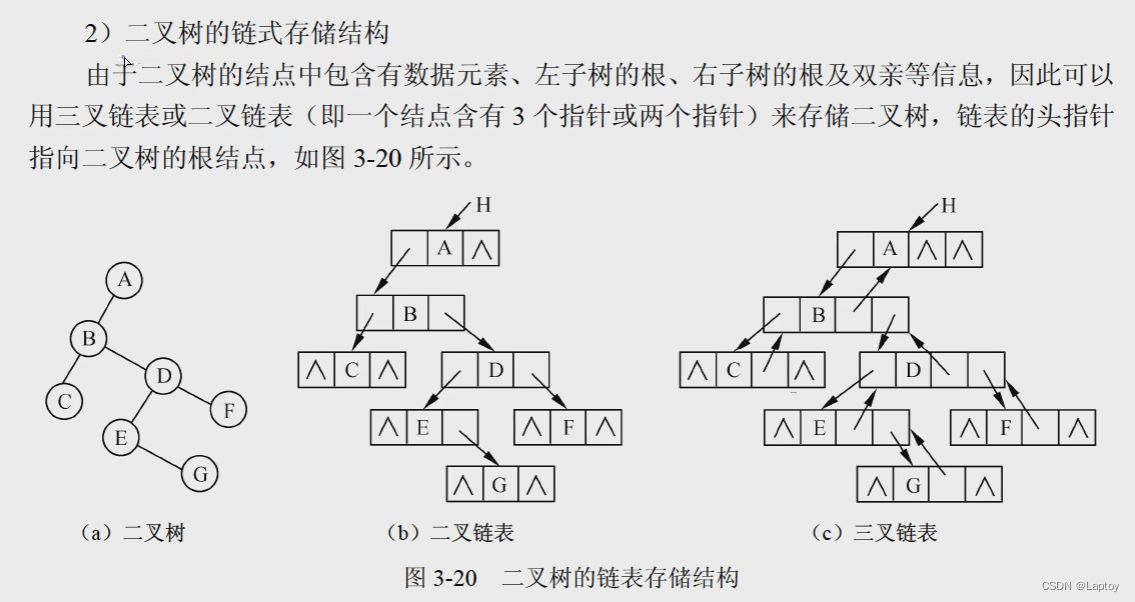
- 二叉链表：空指针n+1个 指向左、右结点
- 三叉链表：空指针n+2个 指向左、右、父结点
二叉树遍历
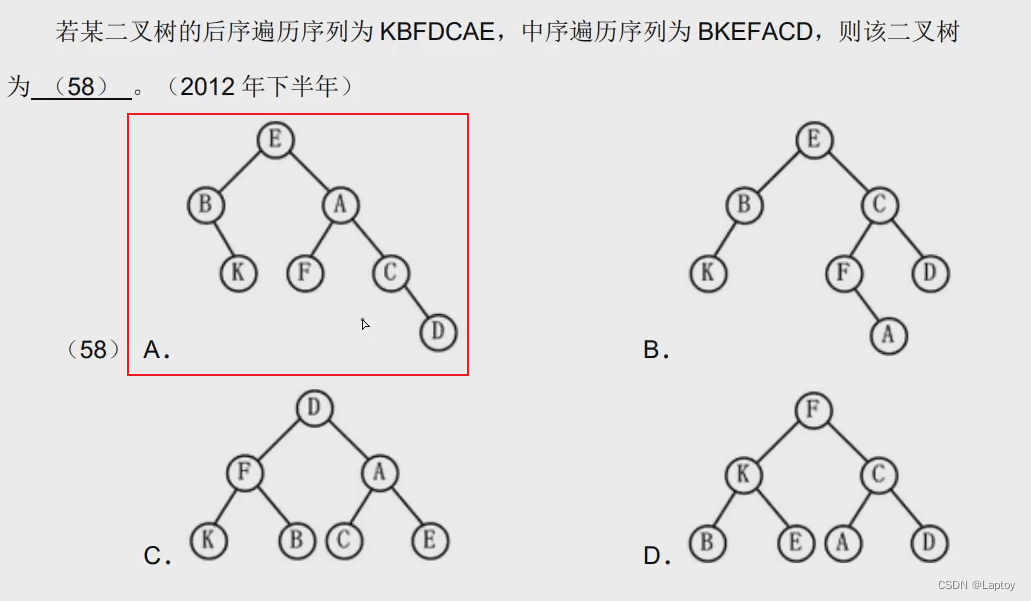
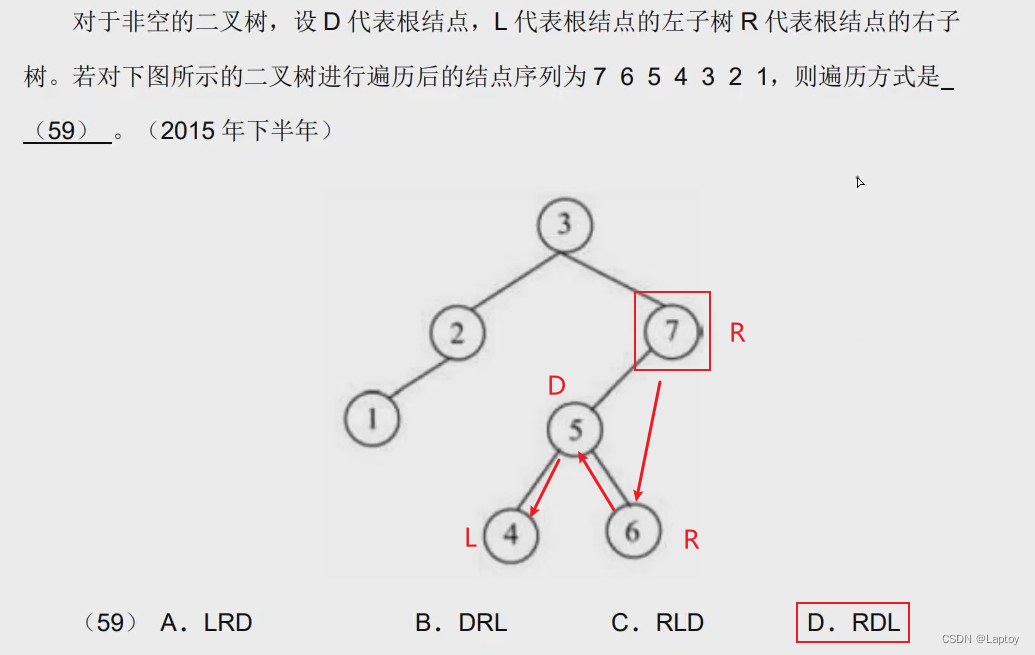
- 先序遍历：根 左 右
- 中序遍历：左 根 右
- 后序遍历：左 右 根
- 层次遍历：从上到下一层一层遍历
中序遍历+任一序遍历可以构造二叉树 必须有中序遍历
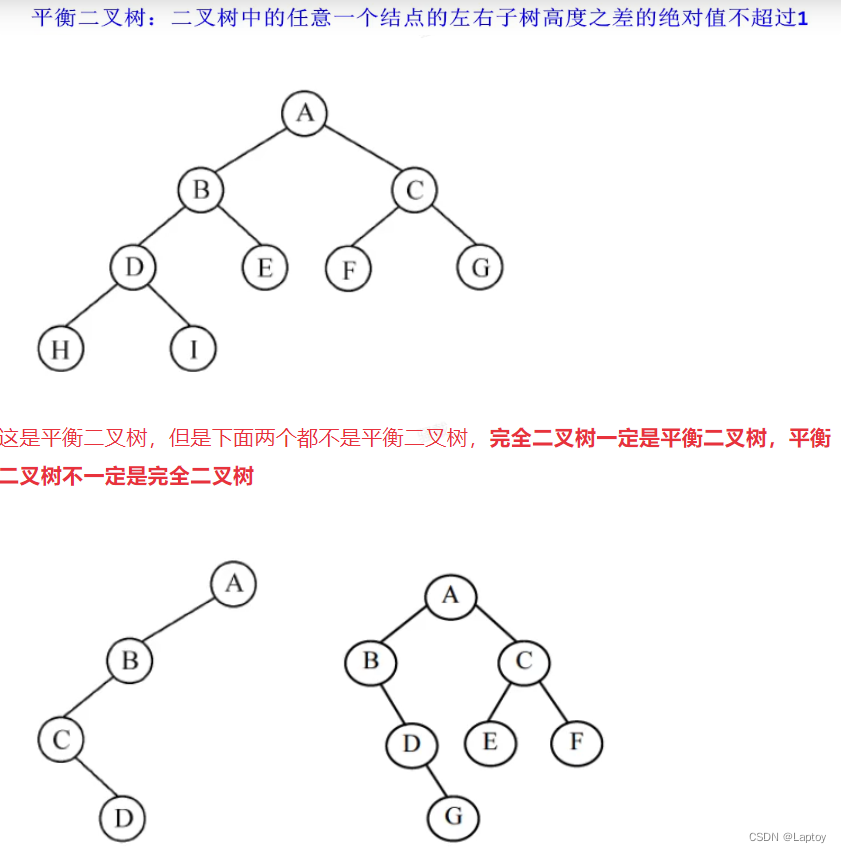
平衡二叉树 一定是完全二叉树
二叉排序树
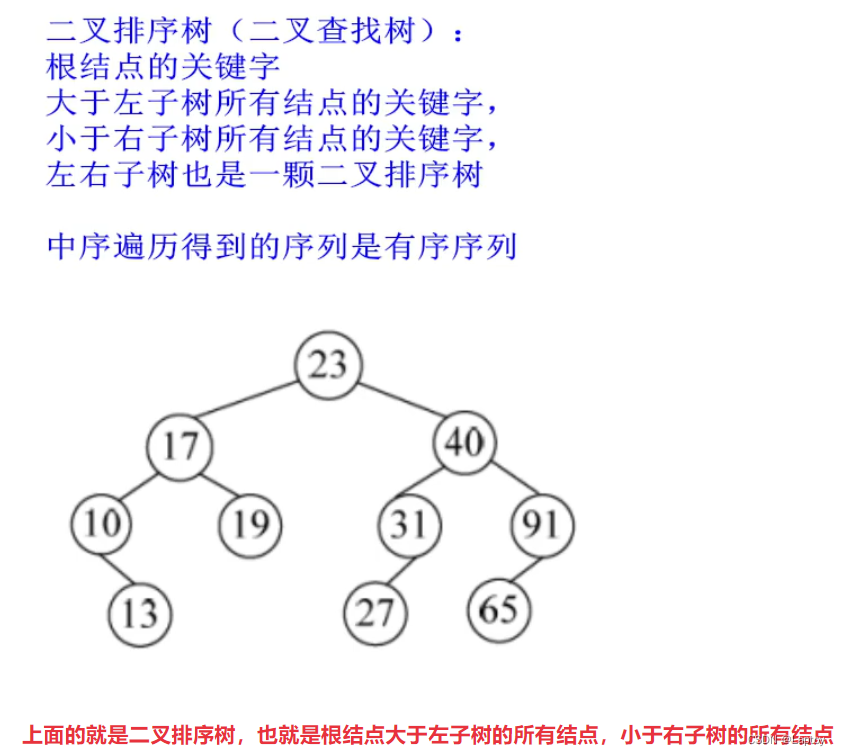
左<根<右
关键字和根结点比较，小于放左边，大于放右边
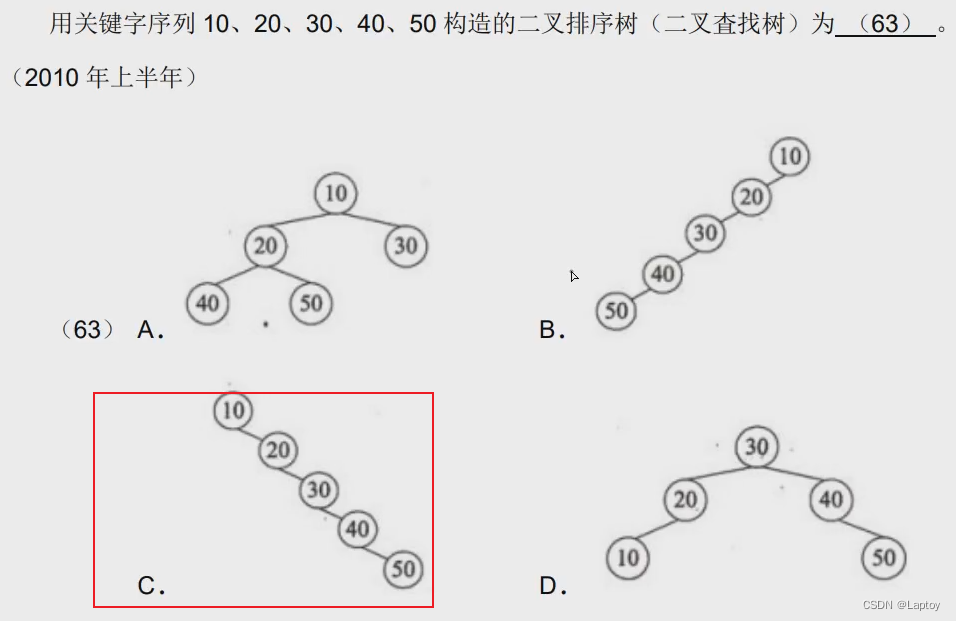
10必须为根结点
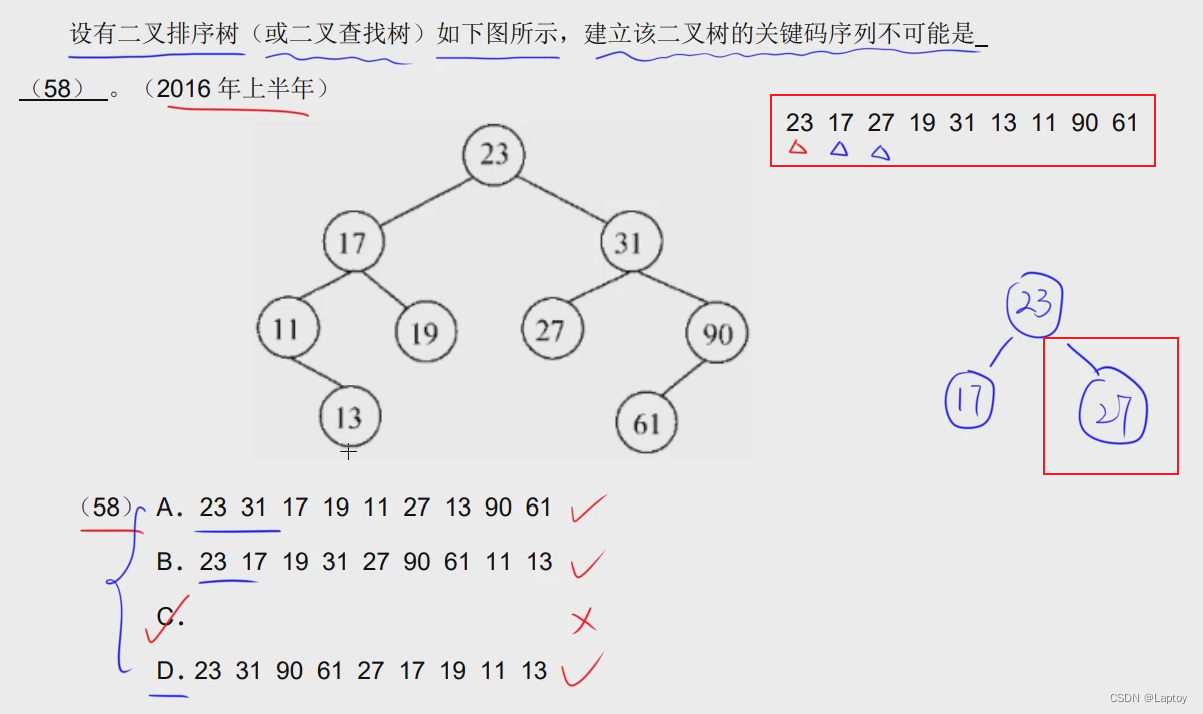
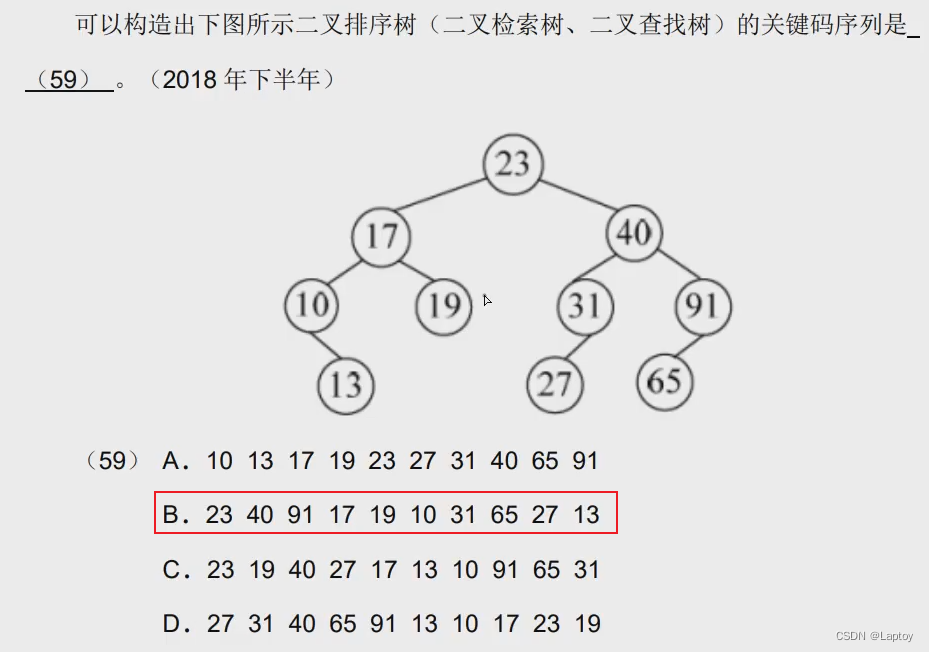
最优二叉树(哈夫曼树)
所有(叶子结点到根结点路径长度*结点的值)之和
和最小的二叉树为最优二叉树(哈夫曼树)
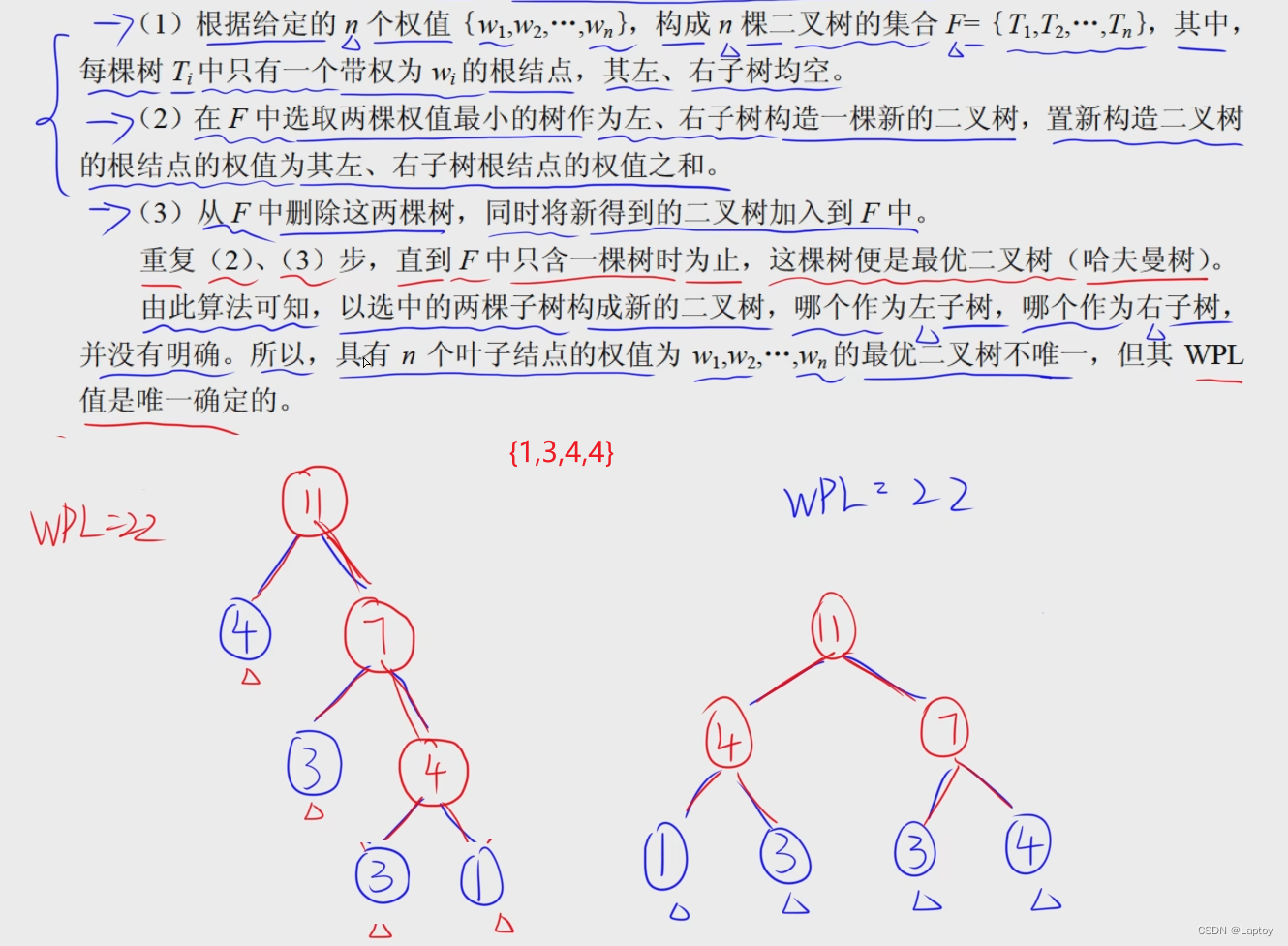
构造的哈夫曼树不唯一，WPL值唯一
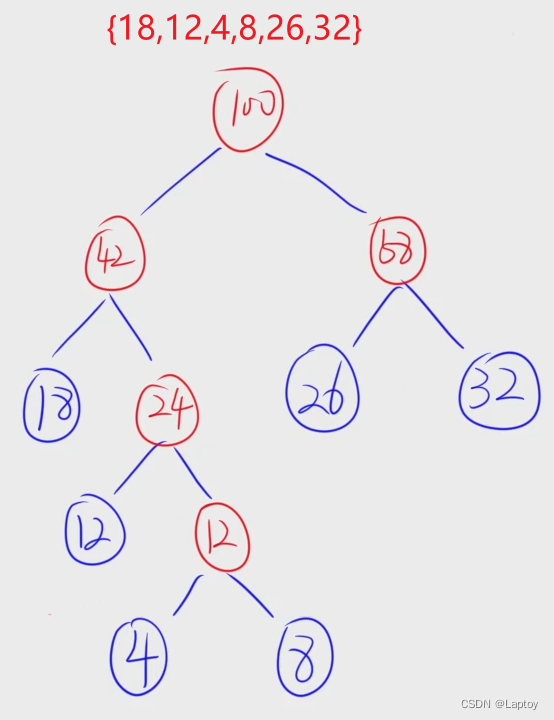
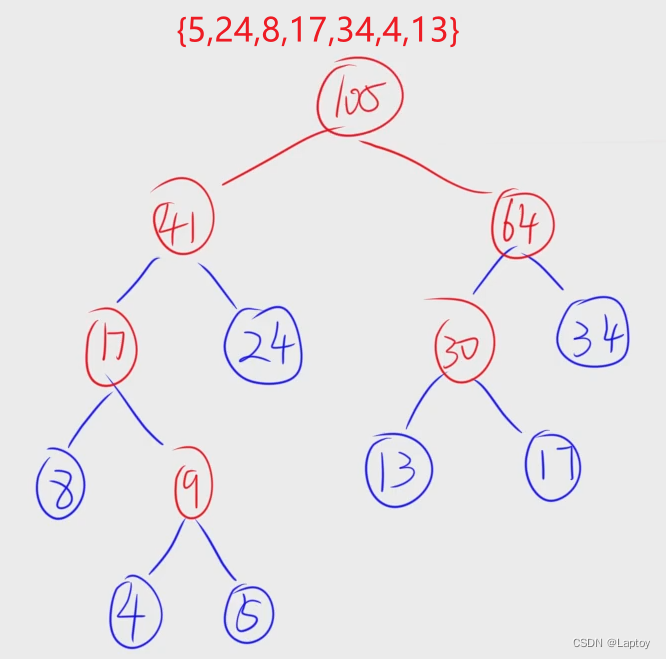
构造哈夫曼树
- 权值越大离根节点越近
- 给定的权值节点为叶子节点
- 每个非叶子节点度都为2
- 总的节点为给定的节点的(2倍-1)
- 从前往后找两个权值最小
- 小左大右加入末尾（若构造完的权值和原本的权值一样，那么构造完的放右边 ）
- 权值相同从前往后
- 用时再调用
哈夫曼编码
暂时跳过
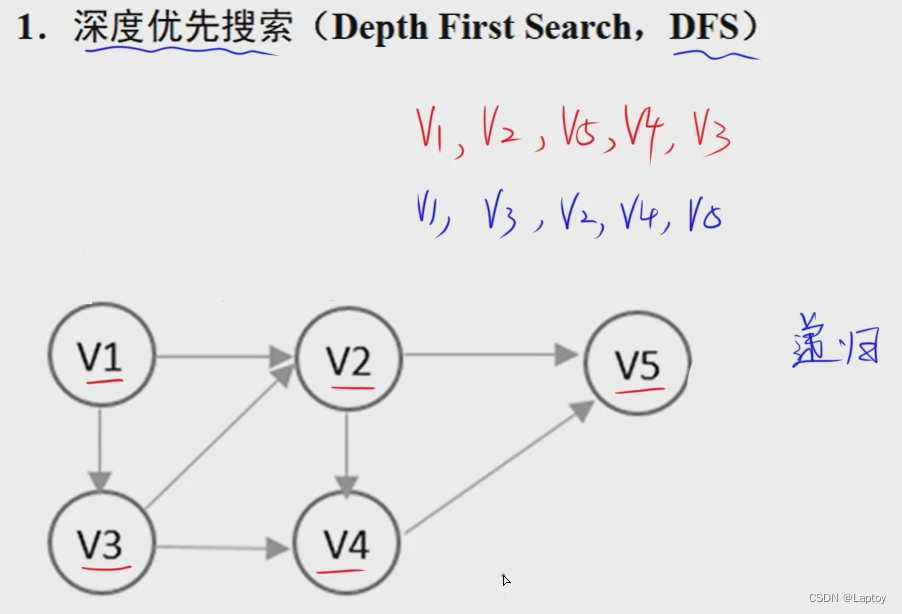
图
暂时跳过
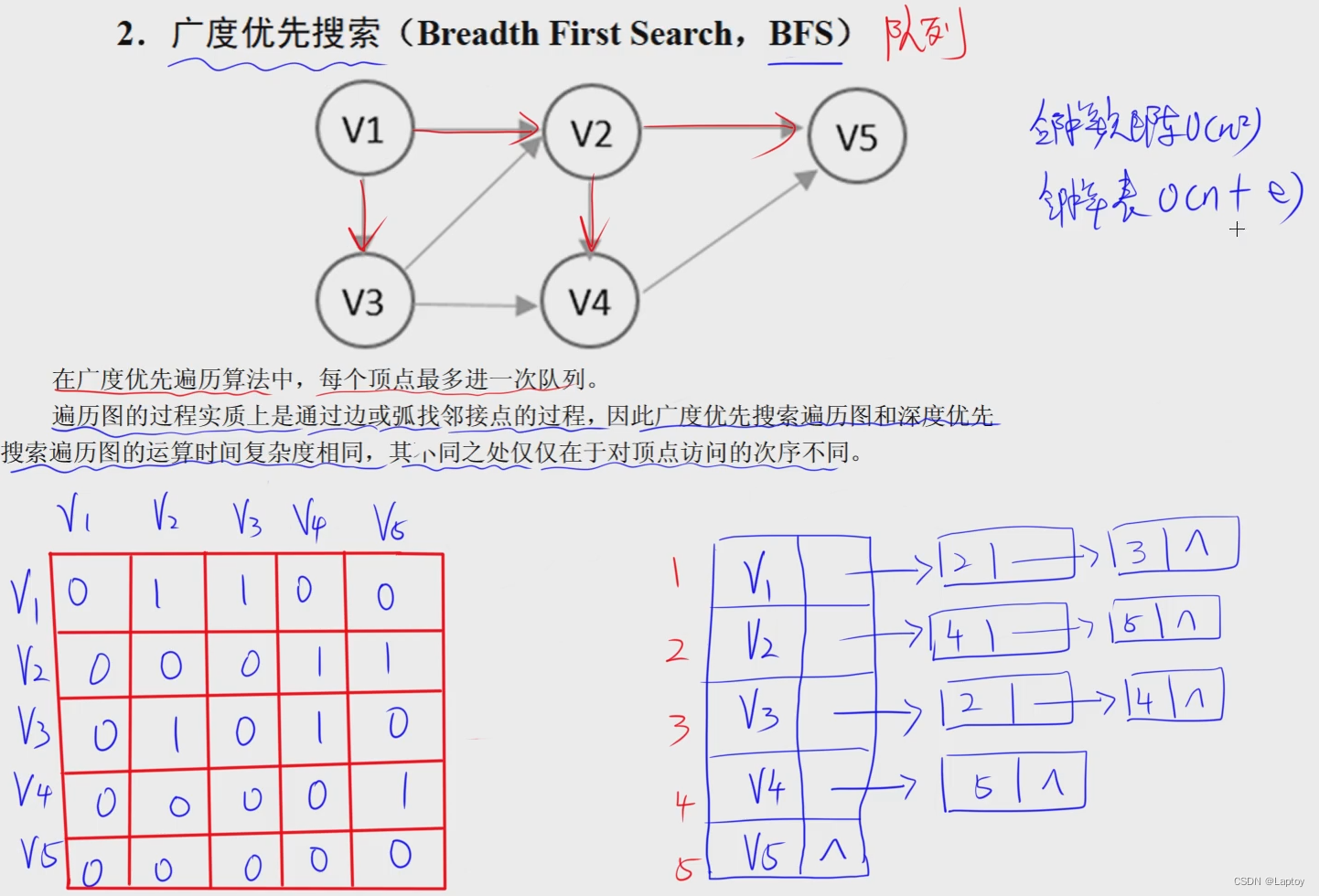
查找
主要考二分查找
顺序查找 顺序/链表存储
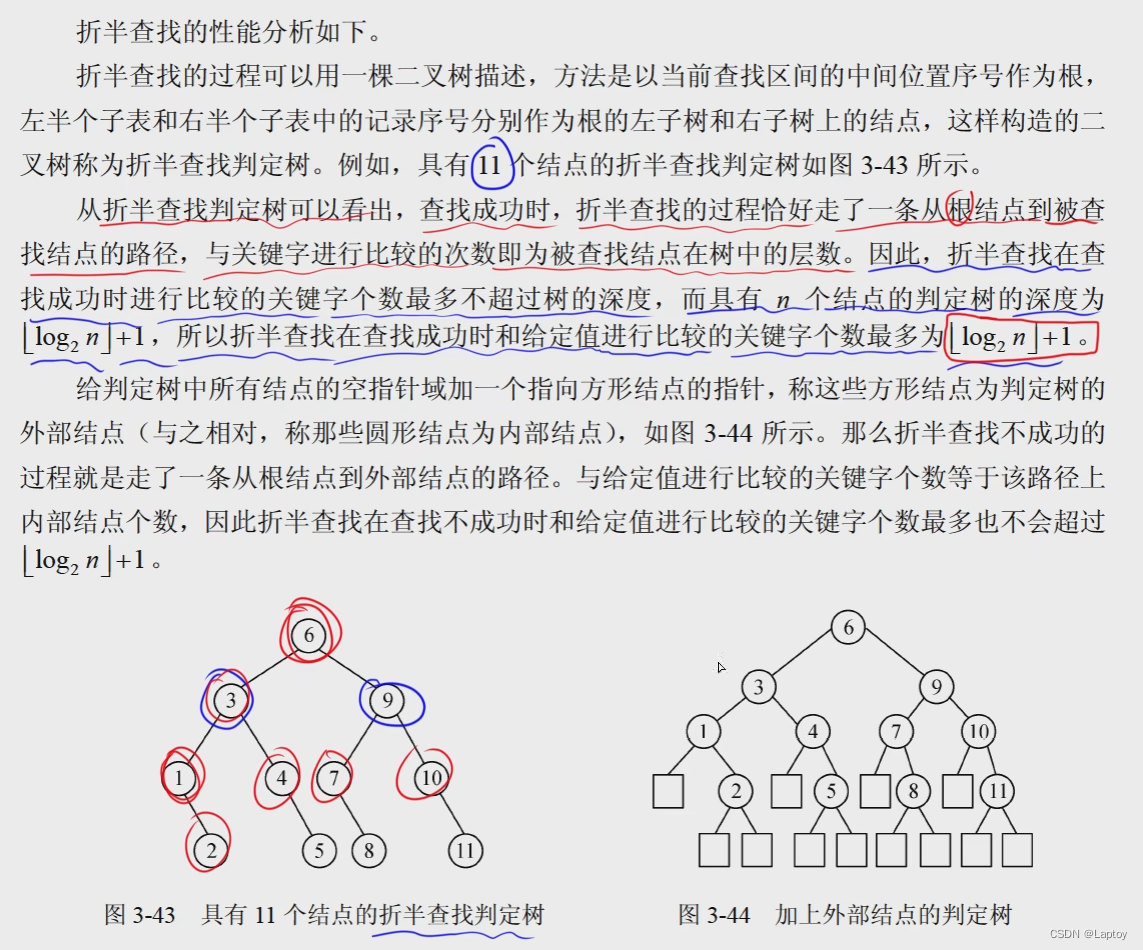
二分查找 顺序存储 有序
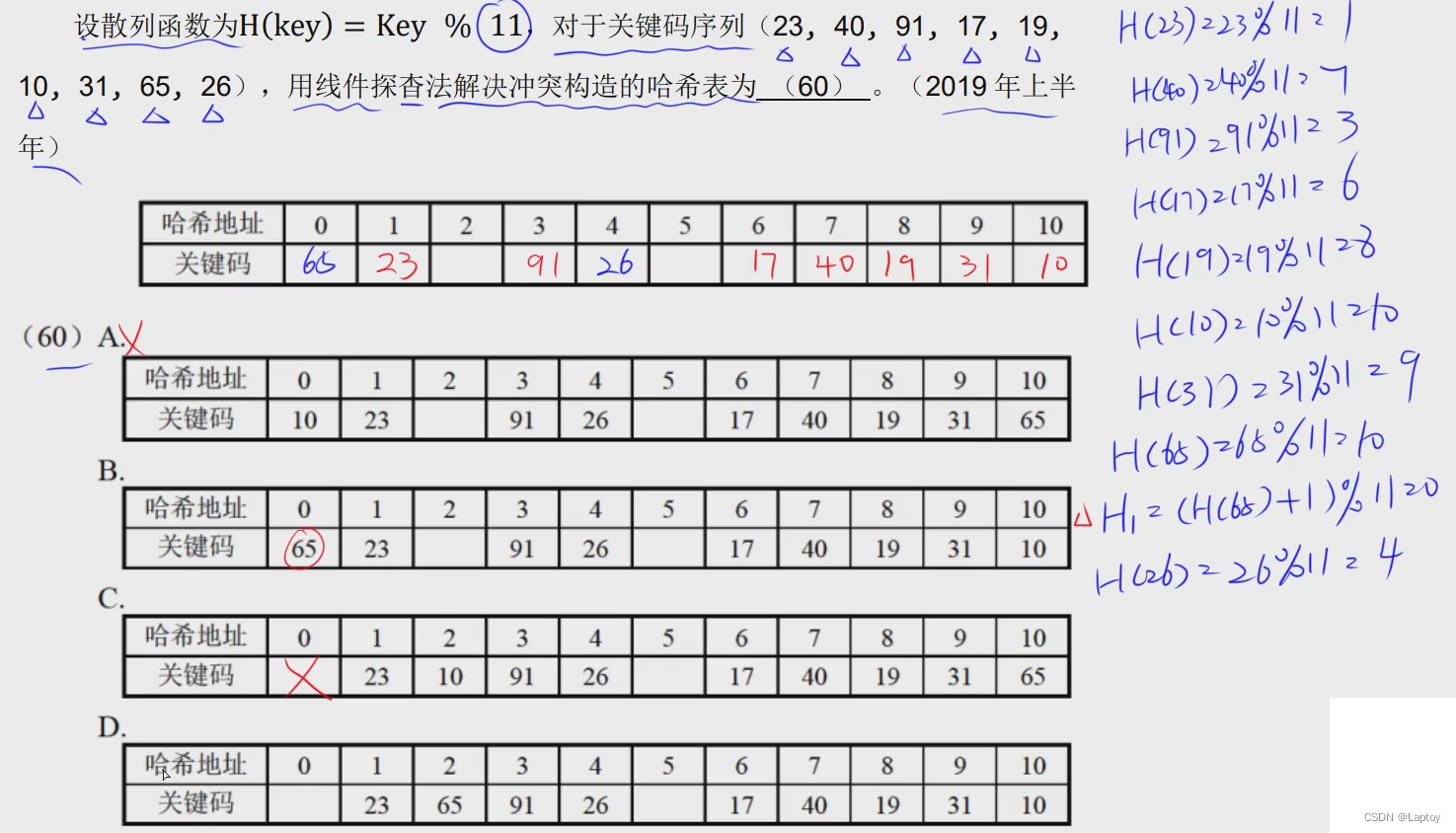
哈希表 HashMap
冲突：不同关键字映射到相同存储位置
计算哈希地址，冲突了就+1再次计算，+2再次计算，直到不冲突
堆 基于完全二叉树
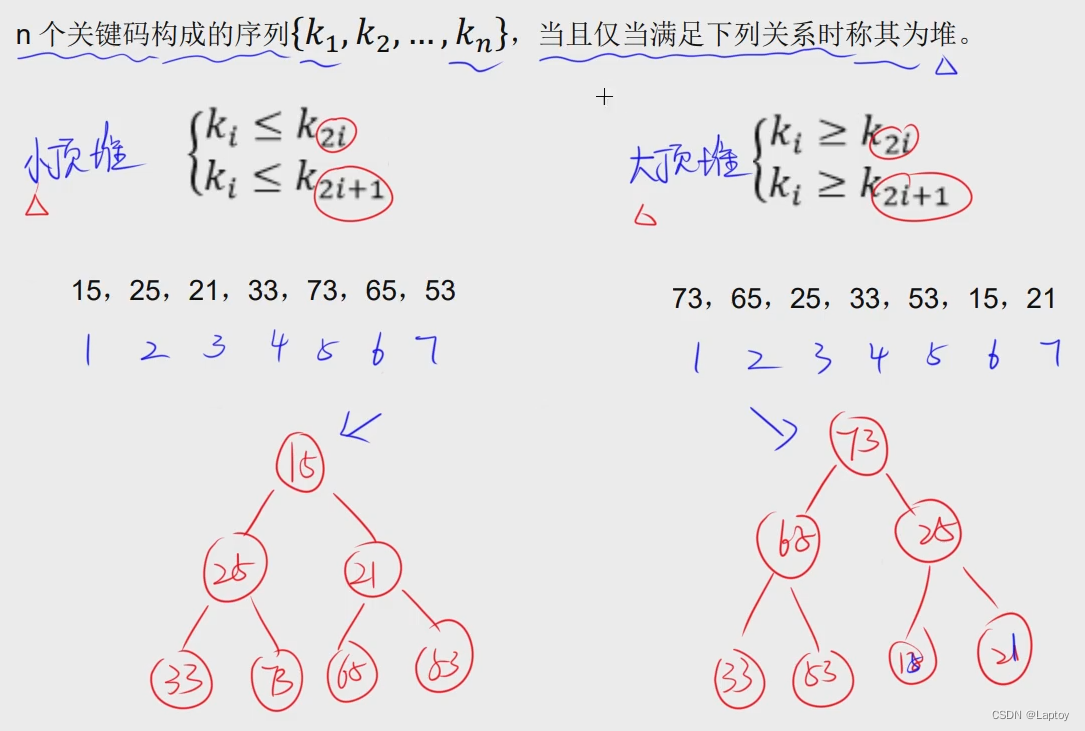
- 大顶堆：父结点大于子结点
- 小顶堆：父结点小于子结点
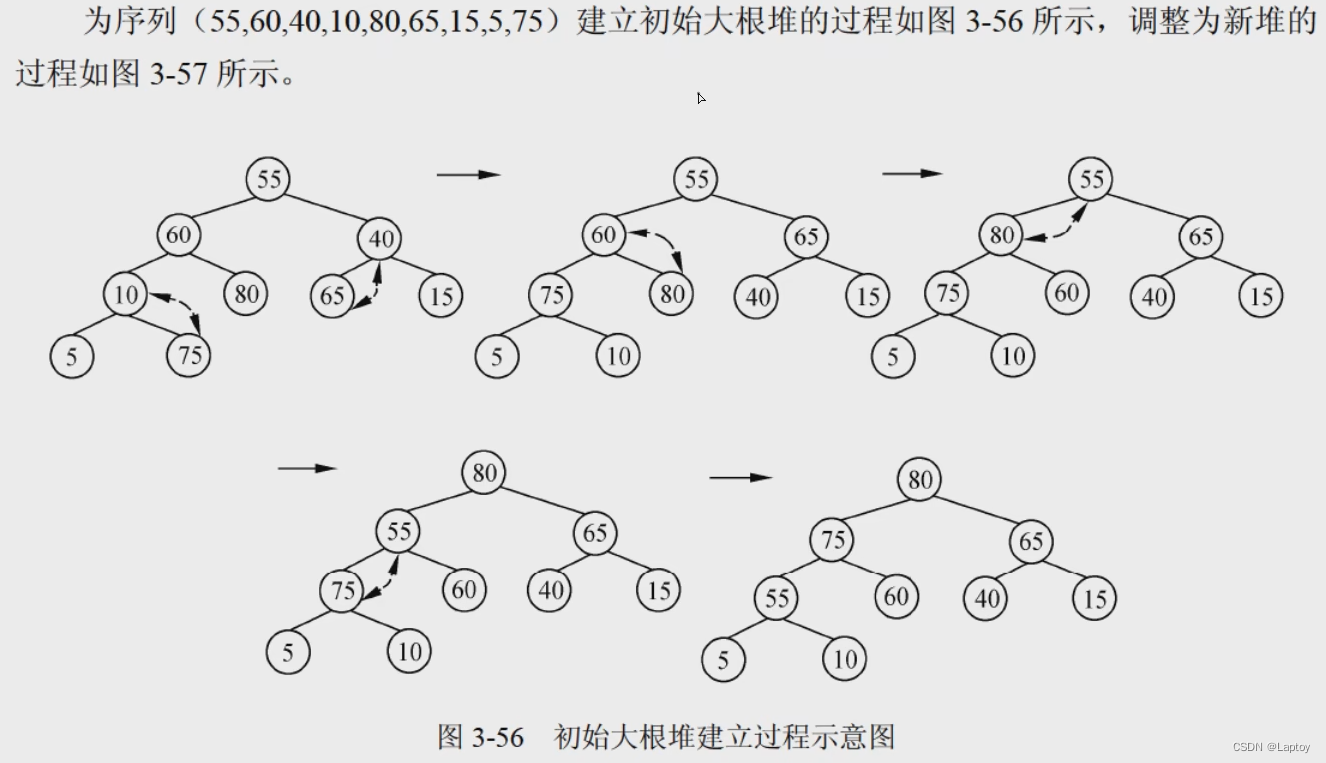
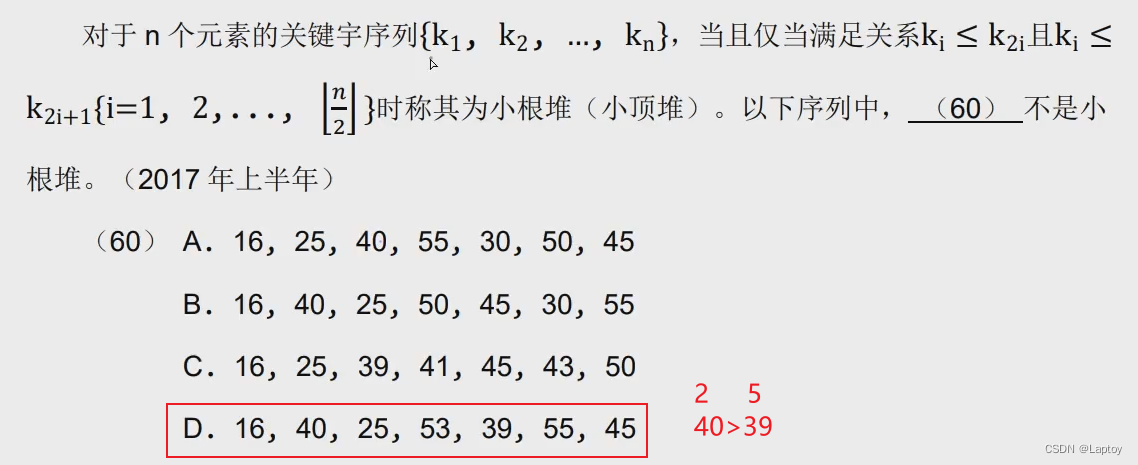
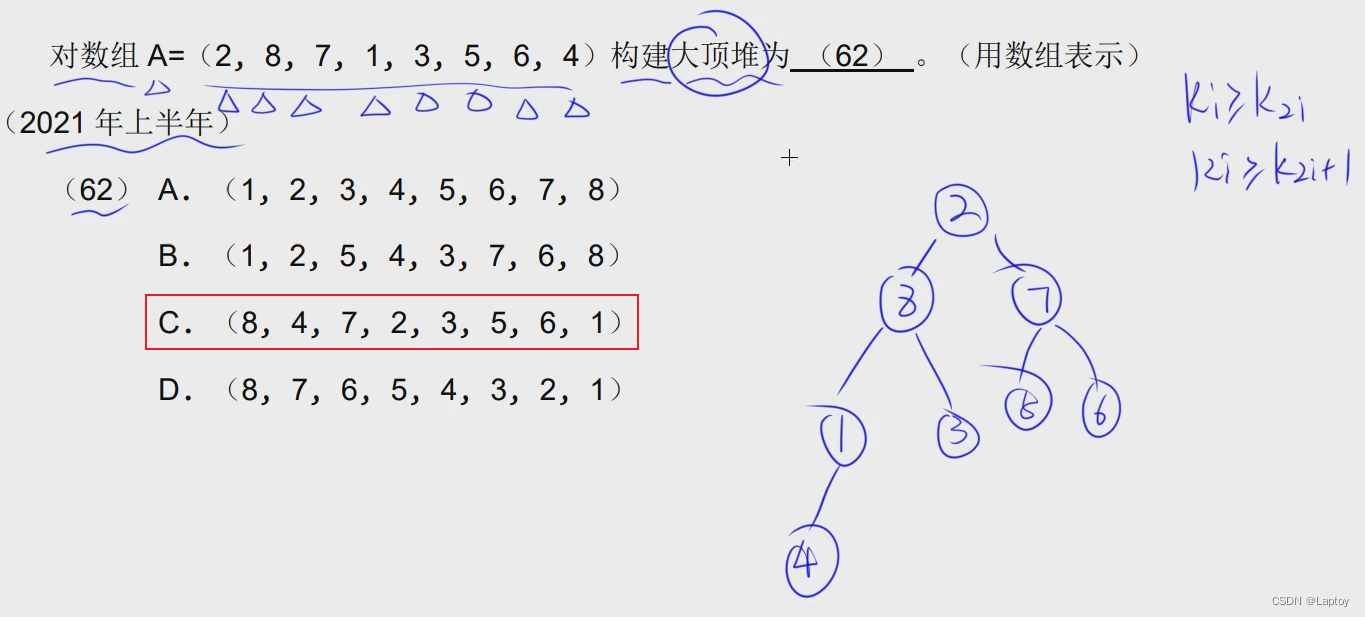
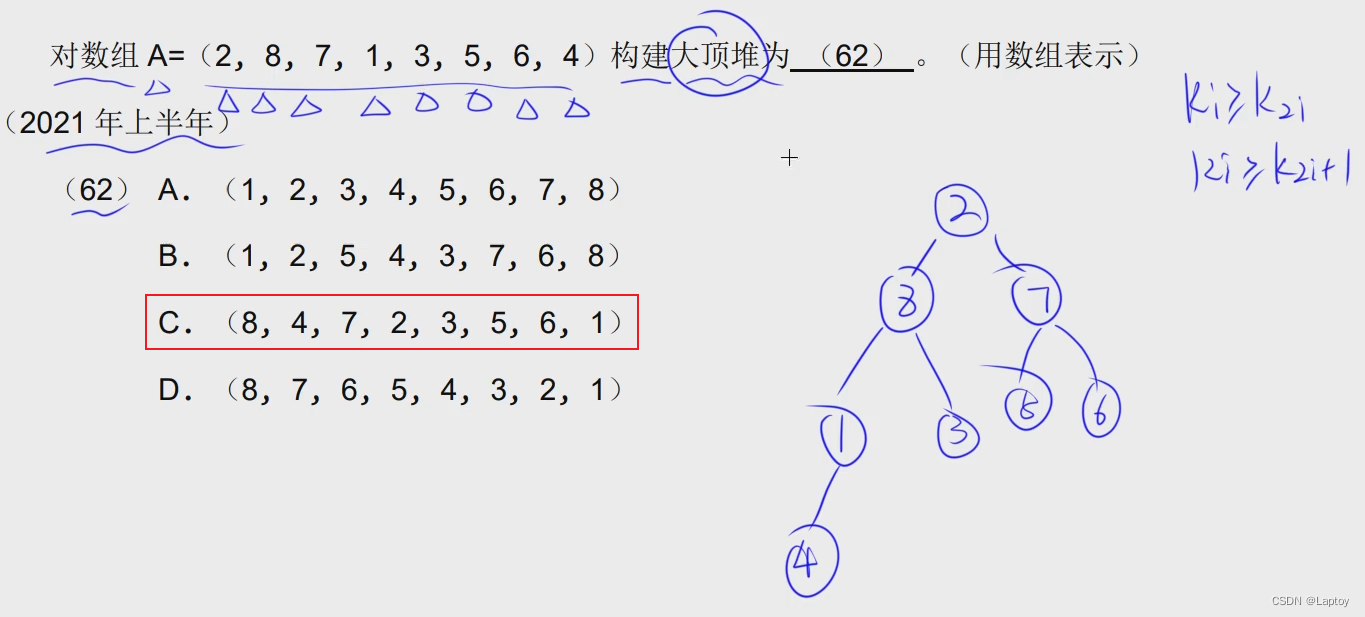
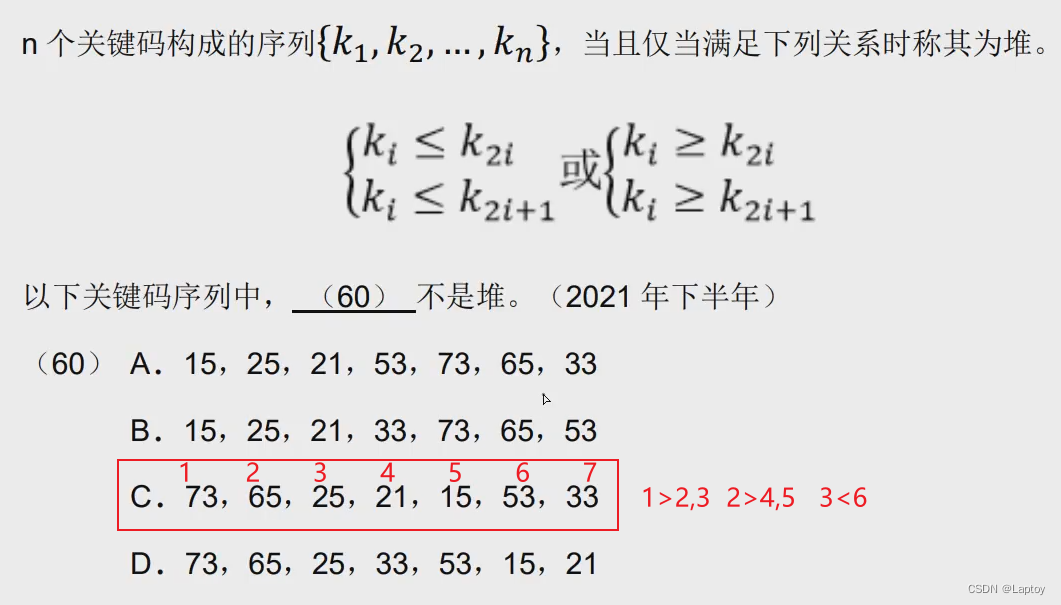
直接代入 k[i]和k[2i] k[2i+1]作比较
